Задача 8. Визначити залежність тиску насиченої пари над краплею від радіуса краплі

Розв’язання. Через поверхневий натяг змінюється умова механічної рівноваги між краплею і насиченою парою біля цієї краплі. Це призводить до залежності тиску насиченої пари краплі від її розміру. Знайдемо цю залежність.

Нехай крапля рідини (фаза (')) має радіус 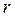і знаходиться в рівновазі з її парою (фаза ('')). Умова рівноваги для нашого випадку береться з (8.32) і має вигляд

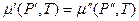. (1)

Тиск в парі 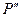відлічуватимемо від тиску 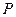для плоскої поверхні поділу, для якої умова рівноваги виражається як

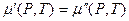. (2)

Через малу стисливість рідини можна наближено записати

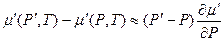(3)

або, враховуючи (8.38), а також, що :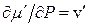

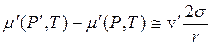, (4)

де 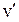- об’єм, який припадає на одну частинку в рідкій фазі.

Вважаючи пару ідеальним газом, її хімічний потенціал 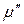можна представити у вигляді

,

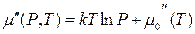звідки

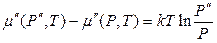(5)

Оскільки ліві частини (4) і (5) збігаються (через рівності (1) та (2)), прирівнюючи їх праві частини, остаточно отримаємо шукану залежність:

.

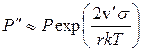З одержаної формули видно, що тиск насиченої пари малих крапель більший, ніж у великих. Тому система з крапель різних розмірів завжди знаходиться в стані нестійкої рівноваги: малі крапді випаровуються, а великі зростають.

Задача 9. Враховуючи питому (молярну) теплоту переходу “рідина-пара” постійною величиною, показати, що тиск насиченої пари змінюється із зміною температури за експоненціальним законом.

Розв’язання. За рівнянням Клапейрона-Клаузіуса (8.42) маємо

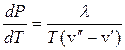, (1)

де 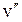- молярний об’єм пари, 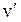- молярний об’єм рідини. Вдалині від критичної точки вважатимемо 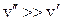. Тому, приймаючи, що насичена пара задовольняє термічному рівнянню стану ідеального газу, (1) можна переписати у вигляді

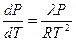. (2)

Інтегруючи (2), одержуємо

,

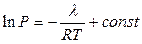звідки остаточно

,

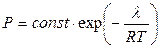що й потрібно було довести.

Задача 10. При низькій температурі теплоємність металів пропорційна . Якщо метал переходить у надпровідний стан, то його теплоємність пропорційна . Показати, що при критичній температурі .

Розв’язання. За умовою можна записати

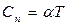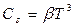, , (1)

де 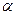, 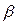- сталі. Використовуючи формулу 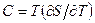, разом з (1) маємо

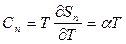(2)

та

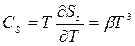. (3)

Інтегруючи (2) та (3), одержимо

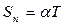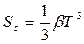, . (4)

Однак, при критичній температурі 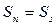(фазовий перехід другого роду), що, повертаючись до (1) і (2), дає .

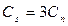8.3. Задачі для самостійного розв’язування

8.1. Визначити умови рівноваги двох фаз різних речовин, тобто двофазної двокомпонентної системи, коли кожний компонент входить до складу тільки однієї фази.

8.2. Визначити умову механічної рівноваги у зовнішньому силовому полі з потенціальною енергією .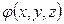

8.3. Одержати формулювання (8.24) закону діючих мас.

8.4. Знаючи константи рівноваги 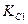і 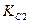для реакцій

,

,

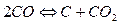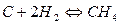знайти константу рівноваги для реакції

.

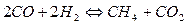8.5. В якій пропорції за числом молів треба змішувати азот і водень, щоб при будь-яких 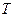і 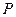в суміші одержувати найбільший (рівноважний) вихід аміаку. Гази вважати ідеальними.

8.6. На прикладі газу Ван-дер-Ваальса показати, що стисливість 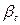і коефіцієнт теплового розширення 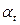в критичній точці перетворюються на нескінченність.

8.7. Три фази однокомпонентної системи 1, 2, 3 знаходяться в рівновазі одна з одною в потрійній точці. Їх питомі об’єми дорівнюють відповідно 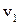, , 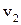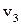. Нехай 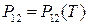, , 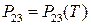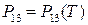- рівняння кривих рівноваги відповідно між газоподібною і рідкою, рідкою і твердою, газоподібною і твердою фазами. Покажіть, що у потрійній точці виконується співвідношення

.

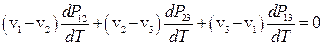8.8. Визначте, як залежить питомий об’єм пари від температури для процесу, при якому пара весь час залишається в рівновазі з рідиною, тобто уздовж кривої рівноваги рідини та її пари. Вважати пару ідеальним газом.

8.9. Визначити молярну теплоємність насиченої пари для процесу, при якому вона весь час залишається насиченою. Пару вважати ідеальним газом.

8.10. Вивести з рівності (8.51) рівняння Еренфеста (8.48) і (8.49).

Розділ 9