Под системой связи понимают совокупность технических средств и среды распространения сигналов, обеспечивающих передачу сообщения от источника к потребителю.
Описание работы схемы:
Рассмотрим назначение отдельных элементов этой схемы и проиллюстрируем происходящие в них процессы соответствующими временными и спектральными диаграммами.
На выходе источника сообщений имеем непрерывное сообщение:
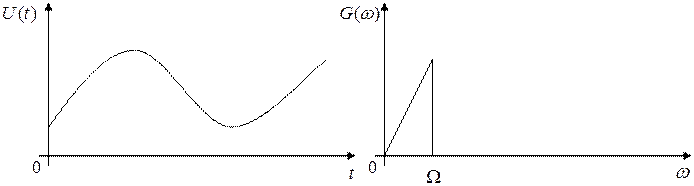
В устройстве преобразования сообщения в сигнал непрерывное сообщение, поступающее с выхода источника, преобразуется в цифровой сигнал. Процесс преобразования состоит из нескольких операций. Сначала непрерывное сообщение подвергается дискретизации по времени:
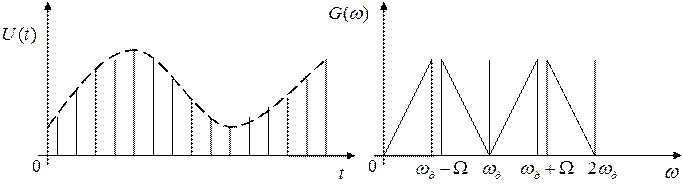
Далее полученная последовательность дискретных отсчетов передаваемого сообщения квантуется, и посредством кодирования представляется в виде последовательности двоичных символов «1» и «0». Такое преобразование называется импульсно кодовой модуляцией (ИКМ), а устройство, где оно происходит называется аналого-цифровым преобразователем (АЦП).
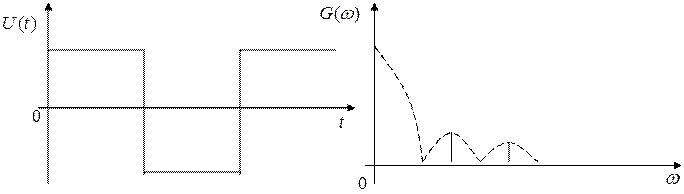
В передатчике происходит модуляция сигнала, в данном случае – это частотная модуляция (ЧМ).
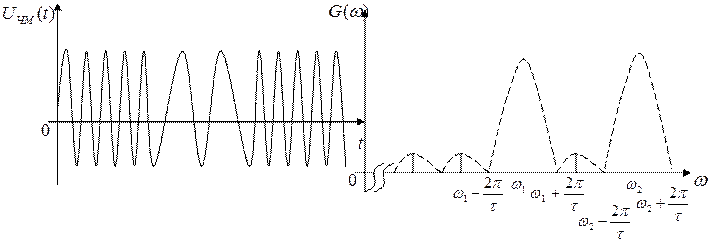
Проходя через линию связи, ЧМ – сигнал подвергается воздействию различного рода помех, и на вход приемника поступает смесь полезного сигнала и помехи.
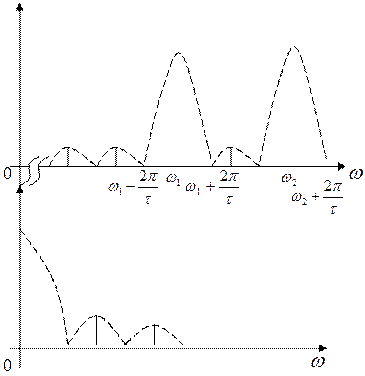 |
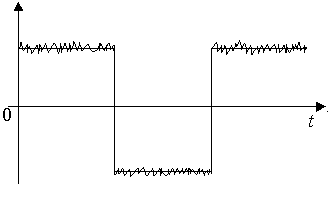
Приемник обрабатывает эту смесь и принимает решение о том, какой сигнал передавался. С выхода приемника сигнал поступает на устройство преобразования сигнала в сообщение. Таким устройством является цифро-аналоговый преобразователь (ЦАП). Здесь происходит преобразование последовательности двоичных символов в квантованную последовательность отсчетов, которые сглаживаются до непрерывного сообщения с той или иной точностью, и к получателю приходит сообщение, подобное сообщению на выходе источника.
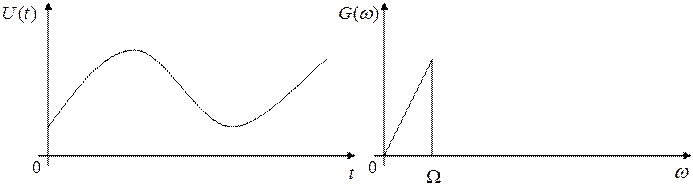
5. Структурная схема приемника.
В соответствии с исходными данными варианта в качестве приемника применяется приемник когерентного приема ДЧМ. При ДЧМ: при передачи “1” передается колебание с одной частотой, а при “0” с другой, при этом на приеме все параметры передаваемого сигнала известны. Задачей приемного устройства является определение степени соответствия поступивших сигналов с эталонными на фоне помех.
Элементами сигнала при ЧМ являются:
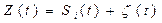 , где i=1,2;
, где i=1,2; 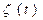 - флуктуационная помеха типа гауссовского шума.
- флуктуационная помеха типа гауссовского шума.
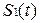 |
 Векторная диаграмма.
Векторная диаграмма. 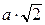 |
S1(t)=Acos
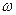 1t
1t  S2(t)=Acos
S2(t)=Acos 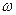 2t S2(t)
2t S2(t)
Вычисление степени соответствия математически записывается следующим образом:
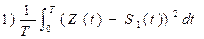
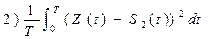
где t – время наблюдения за сигналом,
S1(t), S2(t)- эталонные сигналы
Z(t) – принятый сигнал с помехой
Если Z(t) ближе к одному из эталонных сигналов, то вычисленное значение будет ближе к нулю, таким образом можно записать математическую запись алгоритма принятия решения.
Если на передаче S1(t) и 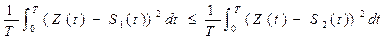 , то приемник принимает решение в пользу S1(t) – алгоритм идеального приемника Котельникова. Если же на передаче S2(t) и
, то приемник принимает решение в пользу S1(t) – алгоритм идеального приемника Котельникова. Если же на передаче S2(t) и 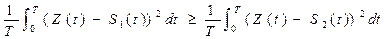 , то приемник принимает решение в пользу S2(t).
, то приемник принимает решение в пользу S2(t).
Раскрыв скобки в математической записи алгоритма принятия решения получим:
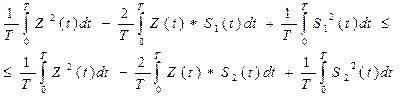
в результате приведения подобных получим:
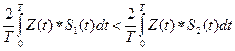 или ВS1 < ВS2
или ВS1 < ВS2
ВSi – функция корреляции, устройство вычисляющее функцию корреляции называют активным фильтром или коррелятором.
На основе последней формулы можно составить схему приемника ДЧМ (рис.3)
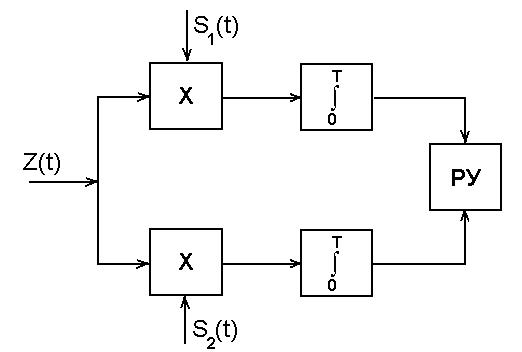
Рис.3 Схема приемника ДЧМ
Схема содержит два перемножителя по числу передаваемых сигналов, два коррелятора (активных фильтра) и решающее устройство (РУ).При приеме сигналов ДЧМ местные генераторы генерируют эталонные сигналы S1(t)=Acos 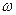 1t и S2(t)=Acos
1t и S2(t)=Acos 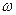 2t.
2t.
В перемножителях поступившие и эталонные сигналы перемножаются. Далее сигналы поступают на коррелятор. Мгновенные значения с выходов интегратора в определенные моменты времени (например, в середине посылки) сравнивается в РУ с некоторым пороговым уровнем Uпорог.. При выполнении неравенства ВS1 > Uпорог регистрируется сигнал S1, в противном случае — S2.
6.Принятие решения приемником по одному отсчету
Сообщения передаются последовательностью двоичных символов "1" и "0", которые появляются с априорными вероятностями соответственно p(1) и р(0). Этим символам соответствуют канальные сигналы S1(t) и S2(t), которые точно известны в месте приема.
В канале связи на передаваемые сигналы воздействует гауссовский стационарный шум с дисперсией s2. Приемник, оптимальный по критерию идеального наблюдателя, принимает решение по одному отсчету смеси сигнала и помехи
Z(t0) = Si (t0 )+ ς(t0)
на интервале элемента сигнала длительности Т.
Критерий минимального среднего риска минимизирует среднюю вероятность ошибки
pош = P(S1)P(х2/S1) + P(S2)P(х1/S2)
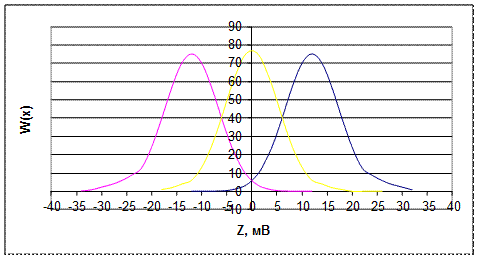
Если бы на входе приемника отсутствовали помехи, мы имели бы дело с "чистыми" сигналами S1 и S2 и задача разделения сигналов была бы очень проста. При наличии же помех сигналы искажаются и для их описания приходится использовать вероятностное пространство. Сами сигналы вместе с помехами описываются уже функциями плотности вероятности w(x/S1) и w(x/S2), которые изображены на рис.4 . На этом же рисунке показан порог хп.
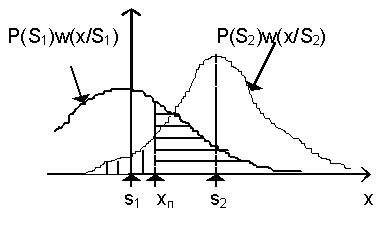
Рис.4
Заштрихованная часть рисунка левее хп имеет площадь, равную
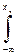 Р(S2)w(x/S2)dx = Р(S2)P(x/S2),
Р(S2)w(x/S2)dx = Р(S2)P(x/S2),
а заштрихованная часть правее хп имеет площадь, равную
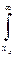 Р(S1)w(x/S1)dx = Р(S1)P(x/S1),
Р(S1)w(x/S1)dx = Р(S1)P(x/S1),
Сумма этих величин, в соответствии с формулой , есть средний риск Rср. Из рис. 4. видно, что Rср будет минимальным, когда минимальна суммарная площадь под кривыми. Это будет в том случае, если величина хп соответствует точке пересечения кривых на рис. . Следовательно, условием получения min{Rср} является такой порог хп, при котором наступает равенство ординат приведенных кривых, т. е.
Р(S1)w(x/S1)dx = Р(S2)w(x/S2),
откуда получаем следующее соотношение:
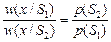 .
.
Стоящее слева выражение называется отношением правдоподобия
l(х) = 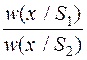 ,
,
Рассчитаем отношение правдоподобия для по исходным данным:
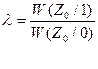 , где
, где
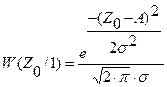
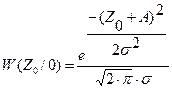
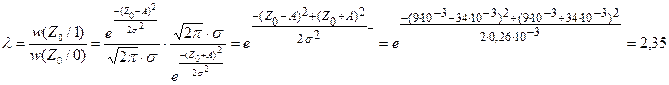
Приемник, использующий отношение правдоподобия сравнивает величин l(х) с l0, (пороговое отношение правдоподобия),если l(х) > l0, приемник выдает сигнал S1, в противном случае сигнал S2. Пороговое отношение правдоподобия определяется по формуле:
l0= 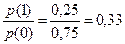 . Следовательно приемник притмет сигнал S1.
. Следовательно приемник притмет сигнал S1.
Рассчитаем и построим функции распределения плотности вероятности для W(ς), W(z/0) и W(z/1).
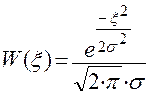 ;
; 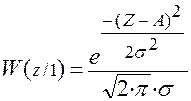 ;
; 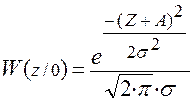 ;
;
Результаты расчета приведены в таблице 1
Таблица 1.
| Z, мВ | -12 | -10 | -8 | -6 | -4 | -2 | -1 | ||||||||
| W(ς) | 6,1 | 13,2 | 24,9 | 40,8 | 71,7 | 75,6 | 76,9 | 75,6 | 71,7 | 40,8 | 24,9 | 13,2 | 6,1 | ||
| W(z/1) | 0,0027 | 0,014 | 0,062 | 0,24 | 0,8 | 2,33 | 3,76 | 5,86 | 8,8 | 12,77 | 24,17 | 39,69 | 56,57 | 69,97 | 75,11 |
| W(z/0) | 75,11 | 69,97 | 56,57 | 39,69 | 24,17 | 12,77 | 8,8 | 5,86 | 3,76 | 2,33 | 0,8 | 0,24 | 0,062 | 0,014 | 0,0027 |
7.Вероятность ошибки на выходе приемника.
При когерентном приёме сигналов ДЧМ на помехоустойчивость влияют только синфазные с сигналом составляющие помех x1 в фильтре w1 и x2 в фильтре w2. Эти составляющие имеют нормальный закон распределения амплитуд с одинаковыми дисперсиями
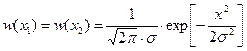 .
.
Вероятность превышения синфазной составляющей помехи в фильтре без сигнала x2 составляющей суммы сигнала и помехи в фильтре с сигналом (a + x1) равна
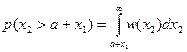 .
.
Для определения средней вероятности ошибки необходимо усреднить вероятность p(x2 > (a + x1)) по всем значениям случайной величины (a+x1), при этом для случая флуктуационной помехи (и симметричного канала связи) получим:
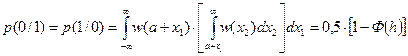 ,
,
где h2 – отношение сигнал / шум.
h2 =Рс/Рп , где Рс- мощность сигнала Si, Рп –мощность помехи.
h2 = А2/2σ2 = (34*10-3)2/2*0,26*10-3 = 2,22 отсюда h = 1,49
Средняя вероятность ошибки равнa
pошЧМкг = 0,5× [ p(0 /1) + p(1/ 0)] = 0,5× [1 – Ф(h)] = 0,067.
Расчет зависимости РошАМ=f(h) для когерентного приема приведен в таблице 2 и показана на рисунке 5.
Таблица 2.
| h | 1,49 | 2,5 | 3,5 | 3,5 | |||
| Pош | 0,5 | 0,158 | 0,067 | 0,027 | 0,0062 | 0,00023 | 0,00023 |
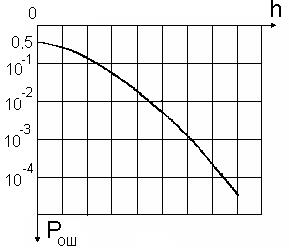
Рис.5 Зависимость вероятности ошибки от соотношения сигнал шум
8.Выигрыш в отношении сигнал/шум при применении оптимального приемника.
При использовании в приёмнике оптимального фильтра вероятность ошибки определяется величиной отношения энергии элемента сигнала к спектральной плотности мощности помехи h02 = Eс / N0 = PсTс/ N0.
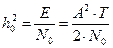 , где
, где
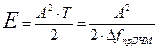 – энергия элемента сигнала (∆fпрДЧМ-полоса пропускания приемника),
– энергия элемента сигнала (∆fпрДЧМ-полоса пропускания приемника),
N0 =σ2/∆fпрДЧМ – спектральная плотность помехи
N0 =σ2/∆fпрДЧМ=0,26*10-3/240000 = 1,08*10-9
Найдем h02
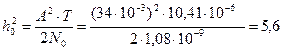 h0=2,4
h0=2,4
Найдем энергетический выигрыш в соотношении сигнал/шум при использовании оптимального приемника, т.е. при оптимальной фильтрации принимаемого сигнала:
h0/h=2,4/1,49 = 1,61

Таким образом, при оптимальной фильтрации соотношение сигнал/шум увеличивается в 1,61 раз.
