Individual tasks for PROBLEM 2.1
THE PRINCIPLE OF MAGNETIC FIELDS’ SUPERPOSITION
In accordance with your variant to solve one of the following problems listed below. The number of problem statement and all necessary input data are reduced in the table 2.1. Necessary drawing is allocated from Figures from problem 2.1.
1 Find magnetic induction, which is created with two infinitely long electric conductors. The picture number, in which the arrangements of conductors are shown, values of current І1 and І2, point, at which magnetic induction should be found, and necessary distances are given at the table. 2.1.
2 Find the magnetic field intensity, which is created with the infinitely long straight conductor and wire loop of radius R. The picture number, in which the situations of a conductor and loop are shown, the values of currents in the conductor І1 and loop І2, point, at which magnetic intensity should be found, and necessary distances are given at the table. 2.1.
3 A current І1 flows along the infinitely long bent wire. The picture number, in which the wire's form is shown, the values of currents and necessary distances are given at the table 2.1. Find the magnetic induction at the point О.
4The infinitely long wire, bent at an angle a, and circular contour of radius of R lie in the same plane. The picture number, in which the situations of contour and wire are shown, values of currents in the wire І1 and contour І2, angle a and necessary distances are given at the table 2.1. Find the magnetic field intensity in the centre of the circular contour.
TABLE OF TASK VARIANTS
Table 2.1
| Variant | Statement number | Picture number* | Point | І1 , А | І2, А | R , sm | а , sm | b , sm | с , sm |
| А | – | – | – | ||||||
| О | – | – | – | – | |||||
| А | – | – | – | ||||||
| О | – | – | – | – | |||||
| О | – | – | |||||||
| В | – | – | |||||||
| О | – | – | – | ||||||
| В | – | ||||||||
| В | – | – | |||||||
| О | – | – | – | – | |||||
| А | – | – | – | ||||||
| О | – | – | – | ||||||
| А | – | – | |||||||
| О | – | – | – | – | |||||
| О | – | – | |||||||
| С | – | – | |||||||
| О | – | – | – | – | |||||
| О | – | – | |||||||
| О | – | – | – | ||||||
| В | – | ||||||||
| О | – | – | – | – | |||||
| А | – | – | |||||||
| О | – | – | – | ||||||
| О | – | – | – | – | |||||
| О | – | – | |||||||
| В | - | - | |||||||
| О | - | - | |||||||
| О | - | - | - | - | |||||
| В | - | ||||||||
| А | - | - |
See Figures for problem 2.1.
FIGURES FOR PROBLEM 2.1 (beginning)
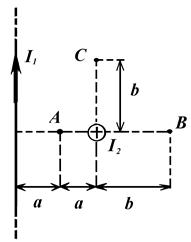 Figure 1 Figure 1 | 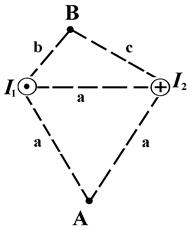 Figure 2 Figure 2 |
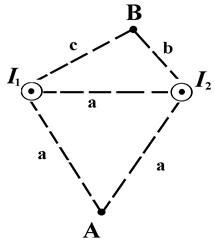 Figure 3 Figure 3 | 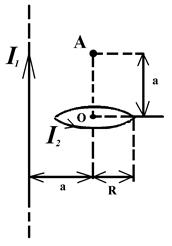 Figure 4 Figure 4 |
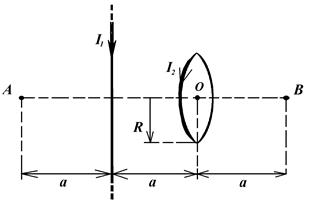 Figure 5 Figure 5 | 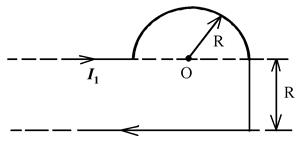 Figure 6 Figure 6 |
FIGURES FOR PROBLEM 2.1 (end)
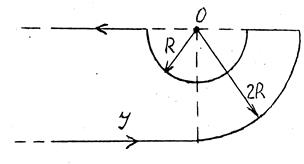 Figure 7 Figure 7 | 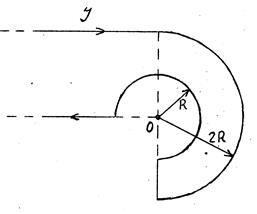 Figure 8 Figure 8 |
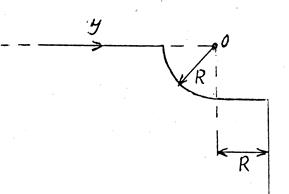 Figure 9 Figure 9 | 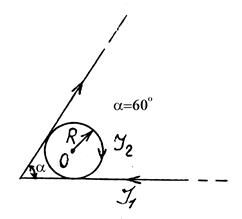 Figure 10 Figure 10 |
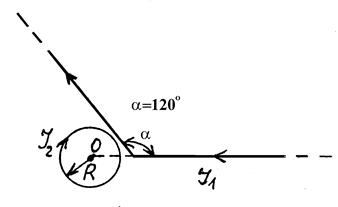 Figure 11 Figure 11 | 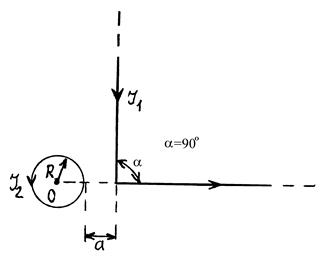 Figure 12 Figure 12 |
Problem 2.4
THE LAW OF ELECTROMAGNETIC INDUCTION
MAIN CONCEPTS
Flux of the vector of magnetic induction 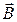 through the plane contour in the homogeneous (uniform) magnetic field
through the plane contour in the homogeneous (uniform) magnetic field
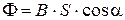 ,
,
where S – area of the contour; α – angel between vector 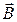 and normal
and normal 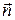 to the plane of the contour.
to the plane of the contour.
Full magnetic flux or magnetic flux interlinkage:
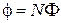 ,
,
where N – the quantity of loops of windings, which are transpierced by the flux F.
EMF of induction in the coil
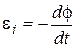 .
.
Charge, which flows over the closed contour by the changing of magnetic flux
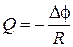 ,
,
where R – resistance of contour.
Magnetic field energy, stored by the coil with the inductance L, through which the current I flows
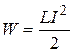 .
.
