Условия ортонормированности

Множество собственных функций любого эрмитового оператора 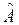образует ортонормированный базис 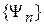. Спектр базиса зависит от 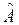и может быть дискретным или непрерывным. Нормировка орта 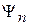зависит от вида спектра n. Ортогональность ортов 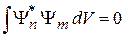при 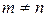и их нормировку объединяет условие ортонормированности.

Дискретный спектр n. Нормировка 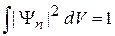следует из условия ортонормированности

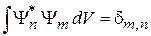, (2.21)

где 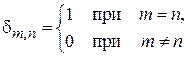– символ Кронекера. Сходимость интеграла 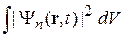требует достаточно быстрого убывания плотности вероятности 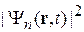за пределами конечного объема, поэтому частица не может неограниченно удаляться. Следовательно, дискретный спектр соответствует связанному состоянию, и наоборот – связанное состояние имеет дискретный спектр энергии и импульса.

Непрерывный спектр n. Если индекс собственной функции принимает непрерывные значения, то в (2.21) вместо символа Кронекера ставится дельта-функция

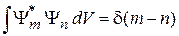. (2.22)

При 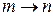интеграл стремится в бесконечность. Плотность вероятности 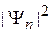конечна во всех точках. Чтобы обеспечить требуемое значение интеграла она не может равняться нулю за пределами любого конечного объема. Следовательно, непрерывный спектр соответствует неограниченному движению, и наоборот – состояние неограниченного движения имеет непрерывный спектр энергии и импульса.