Подставив выражения (6) в уравнения (2b) и (2c) получим

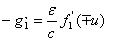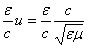но , следовательно, 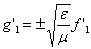или, интегрируя,

.

Электромагнитные волны классифицируются по длине волны 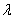или связанной с ней частотой волны 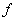. Отметим также, что эти параметры характеризуют не только волновые, но и квантовые свойства электромагнитного поля. Соответственно в первом случае электромагнитная волна описывается классическими законами, изучаемыми в данном томе, а во втором - квантовыми законами, изучаемыми в томе 5 настоящего пособия

Рассмотрим понятие спектра электромагнитных волн. Спектром электромагнитных волн называется полоса частот электромагнитных волн, существующих в природе.

Спектр электромагнитного излучения в порядке увеличения частоты составляют:

Радиоволны;

Инфракрасное излучение;

Световое излучение;

Рентгеновское излучение;

Гамма излучение.

Уравнением квантования момента импульса электрона

, n = 1,2, … ,

Билет 19

1.

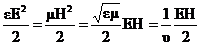
2. Ах, вот оно что, оказывается находим - связь разности фаз колебаний с оптической разностью хода по формуле:

радиан.

3, Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.

4,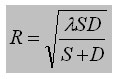

5, Энергетическая светимость тела - - физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот.

; Дж/с·м²=Вт/м²

Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.

7, В координатном представлении волновая функция 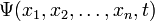зависит от координат (или обобщённых координат) системы. Физический смысл приписывается квадрату её модуля 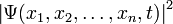, который интерпретируется как плотность вероятности 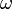(для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами 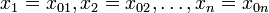в момент времени :

.

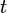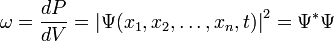Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 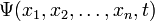, можно рассчитать вероятность 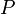того, что частица будет обнаружена в любой области пространства конечного объема :

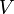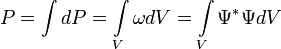
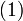
8, Если электрону приписывается собственный механический момент импульса (спин) L_s, то ему соответствует собственный магнитный момент р_ms. Согласно общим выводам квантовой механики, спин квантуется по закону

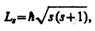
где s — спиновое квантовое число.

Спиновое квантовое число m_s, спин (от англ. spin – кружение, вращение) – характеризует вращение электрона вокруг своей оси и принимает только два значения: +1/2 и –1/2. Электрон со спином +1/2 условно изображают так: ; со спином –1/2: .

10, Волна́ — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры. волновая поверхность — множество точек, имеющих в некий фиксированный момент времени одинаковую фазу колебаний. В зависимости от формы фронта волны выделяют плоские, сферические, эллиптические и другие волны. К волновым свойствам относится пространственная периодичность — скорость изменения фазы (запаздывание процесса во времени) в определённый момент времени с изменением координаты — длина волны λ.

Фа́за колеба́ний — физическая величина, используемая по преимуществу для описания гармонических или близких к гармоническим колебаний, меняющаяся со временем (чаще всего равномерно растущая со временем), при заданной амплитуде (для затухающих колебаний - при заданной начальной амплитуде и коэффициенте затухания) определяющая состояние колебательной системы в (любой) данный момент времени.[3] Равно применяется для описания волн, главным образом - монохроматических или близких к монохроматичности. Волновое число k выражается через длину волны l :

k = 2p / l . (1.7)

Длина волны l равна:

l = cT . (1.8)

Из (1.5), (1.7) и (1.8) следуют соотношения:

k = w/ c и l = c / n .

фазовой скорости:

.

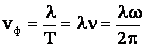Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов, называемая контактной разностью потенциалов. Итальянский физик А. Вольта (1745—1827) установил, что если металлы А1, Zn, Sn, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd привести в контакт в указанной последовательности, то каждый предыдущий при соприкосновении с одним из следующих зарядится положительно. Этот ряд называется рядом Вольта. Контактная разность потенциалов для различных металлов составляет от десятых до целых вольт.

Согласно первому закону Вольта установлено, что при соединении двух различных металлов между ними возникает разность потенциалов, зависящая только от их химического состава и температуры.

Второй закон Вольта гласит: если составить цепь из последовательно соединенных металлических проводников, находящихся при одинаковой температуре, то разность потенциалов между концами цепи не зависит от химического состава промежуточных проводников. Она равна контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников.

Билет 20

1.Ответ - при распространении плоской гармонической электромагнитной волны в однородном веществе с постоянными диэлектрической 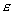и магнитной 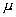проницаемостями напряженности электрического и магнитного полей могут быть записаны с помощью выражений (1.9) , которые с учетом векторных обозначений перепишем в виде :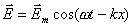

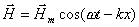
Где 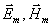векторные амплитуды, определяющие направление колебаний электрического и магнитного полей в электромагнитной волне, распространяющейся в направлении оси 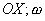частота колебаний волны; 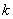волновое число, рассчитываемое в соответствии с (1.9b) и (1.17) по формул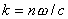е: где 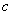скорость света в вакууме 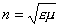показатель преломления среды.

2. Ответ - Электромагнитные волны переносят энергию в соответствии с формулой (бегущая волна) имеет формулу для плотности потока энергии: j=W*v, где j - плотность потока энергии.

Плотность энергии электромагнитной волны представляет собой сумму плотности энергии электрического и магнитных полей: W=WE+WH.

WE=(ε0*E2)/2

WH=(μ0*H2)/2

Модуль плотности потока энергии: П=W*c=E*H

Вектор Умова-Пойнтинга: П=[E H] (все вектора)

3. Ответ - Ширина интерференционной полосы определяется, как расстояние между соседними интерференционными максимумами или минимумами, интерференционные порядки которых отличаются на единицу. Для рассматриваемой интерференционной картины двух источников волн одинаковой интенсивности в соответствии с выражениями (4.9) ширина полосы 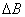оказывается равной: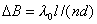

Из этой формулы следует, что расстояние между интерференционными полосами растёт при уменьшении 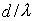. Кроме того, если расстояние до экрана соизмеримо с расстоянием между щелями 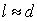,то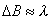

Ответ - Двойное лучепреломление объясняется анизотропностью кристаллов. В кристаллах некубической системы диэлектрическая проницаемость e оказывается зависящей от направления. Как известно, показатель преломления

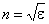Следовательно, из анизотропности e вытекает, что электромагнитным волнам с различными направлениями колебаний вектора 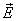соответствуют разные значения показателя преломления 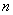.Поэтому скорость световых волн зависит от направления колебаний светового вектора 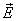.В обыкновенном луче колебания светового вектора происходят в направлении, перпендикулярному к главному сечению кристалла, поэтому при любом направлении обыкновенного луча 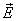образует с оптической осью кристалла прямой угол и скорость световой волны будет одна и та же, равная 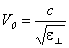. Одноосные кристаллы характеризуются показателем преломления обыкновенного луча, равным 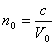и показателем преломления необыкновенного луча, перпендикулярного к оптической оси, равным 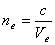. Последнюю величину называют просто показателем преломления необыкновенного луча. Для исландского шпата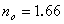 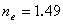. Заметим, что значения 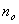и 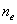зависят от длины волны. С точки зрения принципа Гюйгенса при двойном лучепреломлении в каждой точке поверхности волны, достигающей грани кристалла, возникает не одна, как в обычных средах, вторичная волна, а одновременно две волны, которые и распространяются в кристалле.

5. Ответ - Закон Кирхгофа В соответствии с таким принципом детального равновесия, отношение испускательной и поглощательной способностей одинаково для всех тел в природе, включая абсолютно черное тело, и при данной температуре является одной и той же универсальной функцией частоты (длины волны). 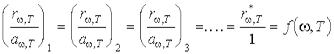или 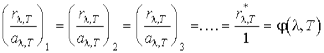где индексы 1, 2, 3... соответствуют различным реальным телам. Из закона Кирхгофа следует, что универсальные функци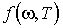и и 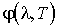есть спектральные испускательные способност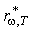и и 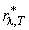абсолютно черного тела по шкале частот или длин волн, соответственно.

6. Ответ - КОМПТОНА ЭФФЕКТ, изменение длины волны, сопровождающее рассеяние пучка рентгеновских лучей в тонком слое вещества. При рассеянии фотона на покоящемся электроне частоты фотона 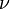и 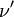(до и после рассеяния соответственно) связаны соотношением:

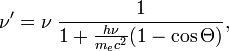где 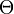— угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн: 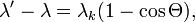где 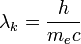— комптоновская длина волны электрона. Для электрона 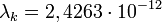.Уменьшение энергии фотона после комптоновского рассеяния называется комптоновским сдвигом.

7. Ответ - Для электрона, ускоряемого разностью потенциалов 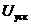, 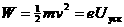откуда 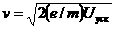теперь можно найти импульс и вычислить дебройлевскую длину волны: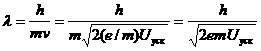

Ответ - Спин — собственный момент импульса элементарных частиц, имеющий квантовую природу и не связанный с перемещением частицы как целого. Спином называют также собственный момент импульса атомного ядра или атома; в этом случае спин определяется как векторная сумма (вычисленная по правилам сложения моментов в квантовой механике) спинов элементарных частиц, образующих систему, и орбитальных моментов этих частиц, обусловленных их движением внутри системы.

II уровень

10.(не полный) Ответ - Первый постулат Бора: атомная система может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия. В стационарных состояниях атом не излучает. Второй постулат: При переходе атома из одного стационарного состояния в другое, излучается или поглощается квант с энергией, равной разности энергий этих состояний.

Де Бройль предположил, что двойственной природой обладает не только свет, но и любой мат. объект. Длина волны любого движущегося объекта: 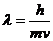В случае наблюдения за объектами микромира: воздействие на них фотона (для определения координаты), ее скорость меняется.

Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровоским радиусом (а), равен .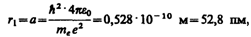

11. ???

Билет 21