ПРИЛОЖЕНИЕ А. Формула Резерфорда
Когда α-частица пролетает вблизи ядра, на нее действует кулоновская сила отталкивания
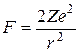 .
.
 В этом случае траектория частицы представляет собой гиперболу. Обозначим буквой θ угол между асимптотами гиперболы (рис. А), характеризующий отклонение частицы от первоначального направления (угол рассеяния). Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем сильнее она рассеивается (тем больше θ).
В этом случае траектория частицы представляет собой гиперболу. Обозначим буквой θ угол между асимптотами гиперболы (рис. А), характеризующий отклонение частицы от первоначального направления (угол рассеяния). Расстояние b от ядра до первоначального направления полета α-частицы называется прицельным параметром. Чем ближе пролетает частица от ядра (чем меньше b), тем сильнее она рассеивается (тем больше θ).
Если считать рассеивающее атомное ядро бесконечно тяжелым, то из закона сохранения энергии следует, что вдали от ядра импульс рассеянной α-частицы р по модулю будет таким же, как и импульс до рассеяния р0. Следовательно, модуль приращения импульса α-частицы, возникающего в результате рассеяния
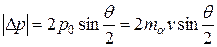 , (А.1)
, (А.1)
где v – начальная скорость частицы, mα – ее масса. Согласно 2-му закону Ньютона,
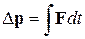 .
.
Спроектировав фигурирующие в этом равенстве векторы на направление Δp, получим:
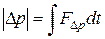 . (А.2)
. (А.2)
Из рис. A видно, что проекция силы F на направление вектора Δp равна Fcosψ. Угол ψ можно выразить через полярный угол φ и угол рассеяния θ:
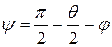 .
.
Следовательно
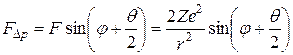 .
.
Подставим это выражение в (А.2), выразив dt как dφ/ 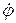 (здесь точка означает дифференцирование по времени):
(здесь точка означает дифференцирование по времени):
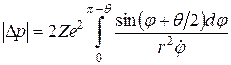 . (А.3)
. (А.3)
Произведение 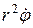 равно M/mα, где M – момент импульса α-частицы, взятый относительно рассеивающего ядра. Кулоновская сила, действующая на α-частицу, является центральной. Поэтому момент импульса остается все время постоянным и равным своему первоначальному значению mαvb. Тогда после замены
равно M/mα, где M – момент импульса α-частицы, взятый относительно рассеивающего ядра. Кулоновская сила, действующая на α-частицу, является центральной. Поэтому момент импульса остается все время постоянным и равным своему первоначальному значению mαvb. Тогда после замены 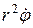 на vb интеграл (А.3) легко вычисляется:
на vb интеграл (А.3) легко вычисляется:
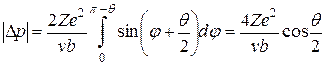 . (А.4)
. (А.4)
Сопоставляя (А.1) и (А.4), найдем, что
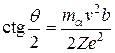 . (А.5)
. (А.5)
Рассмотрим слой рассеивающего вещества настолько тонкий, чтобы каждая α-частица при прохождении через него пролетала вблизи только одного ядра, т.е. претерпевала лишь однократное рассеяние. Чтобы рассеяться на угол, лежащий в пределах от θ до θ+dθ, частица должна пролететь вблизи одного из ядер по траектории, прицельный параметр которой заключен в пределах от b до b + db, причем dθ и db, как это следует из (А.5), связаны соотношением
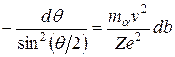 . (А.6)
. (А.6)
Знак «минус» в (А.6) обусловлен тем, что с увеличением b угол рассеяния убывает. Но так как далее нас будет интересовать лишь абсолютное значение db в функции от θ и dθ, знак минус учитывать не будем.
Обозначим площадь поперечного сечения пучка α-частиц буквой S. Тогда количество атомов рассеивающей фольги на пути пучка равно nSa, где n – число атомов в единице объема, a – толщина фольги. Если считать, что α-частицы распределены равномерно по сечению пучка и число их велико, то количество частиц dN, пролетающих вблизи одного из ядер по траектории с прицельным параметром от b до b+db, будет равно
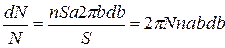 , (А.7)
, (А.7)
где N – общее количество частиц в пучке.
Выразив в (А.7) b и db через θ и dθ в соответствии с (А.5) и (А.6), получим
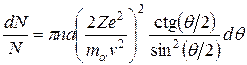 .
.
Далее преобразуем множитель, содержащий угол θ; тогда
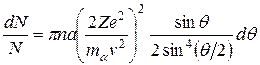 .
.
Выражение 2πsinθdθ есть телесный угол dΩ, в пределах которого заключены направления, соответствующие углам рассеяния от θ до θ+dθ. Учитывая, что кинетическая энергия α-частицы Tα = mαv2/2, окончательно получаем
 . (1.2)
. (1.2)
