Визначення питомого заряду електрона методом магнітного фокусування. 3 страница

dF = I BdL sinα, (1)

де α - кут між напрямком струму та вектором індукції магнітного поля. Сила dF перпендикулярна до площини, що містить елемент I, dL і вектор В, і спрямована в бік, звідки видно найкоротший поворот від елемента струму до вектора В проти годинникової стрілки. Струм зумовлений переміщенням заряджених часток, тому природно допустити, що сила, діюча на провідник зі струмом, зумовлена силами, що діють з боку магнітного поля на окрему рухом заряджену частку. Дійсно, якщо струму в провідникові немає, то заряджені частки рухаються невпорядковано, і сили, що діють на них з боку магнітного поля, мають безладні орієнтації. При складанні таких сил результуюча при великій кількості складових буде невеликою, бо середня сила, що діє на окрему частку, є незначною.

При впорядкованому русі заряджених часток, яким і є електричний струм, з’являється спільна для всіх зарядів складова швидкості, тому в цьому випадку і одержується помітна величина сили, діючої з боку магнітного поля на електричний струм. Відповідні міркування приводять до співвідношення для сили, що діє з боку магнітного поля на відокремлений рухомий заряд, у вигляді:

F = q u B sin α, (2)

де q - величина заряду, u - так звана дрейфова швидкість його.

Співвідношення (2) вперше було одержано Г. Лоренцом. Тому силу, діючу на рухомий заряд з боку магнітного поля , називають силою Лоренца.

Сила Лоренца перпендикулярна до напрямку швидкості, тому вона змінює тільки її напрямок, не змінюючи величину u. Звідси випливає важливий висновок: робота сили Лоренца дорівнює нулю, тобто постійне магнітне поле не здійснює робогти при переміщенні зарядженої частки і не змінює її кінетичної енергії.

Для визначення питомого заряду електрона (так називають відношення e/m, де e і m - відповідно заряд і маса електрона, в даній роботі застосовується метод фокусування електронного пучка повздовжнім магнітним полем.

Рис.1.

Розглянемо рух електрона в магнітному полі. Нехай електрон летить зі швидкістю u, що складає кут α з напрямком магнітного поля В. Розкладемо швидкість електрона на дві складові: вздовж поля u₁=u^.cosα і перпендикулярно полю u₁=u^.cosα (рис.1).

Сила Лоренца на повздовжню складову не діє і змінює тільки напрямок поперечної складової. Оскільки u₂, В і кут α між u₂ і В (прямий!) залишаються сталими, то електрон в площині, перпендикулярній В, буде описувати коло. Сила Лоренца стане доцентровою по відношенню до u₂. Із того, що mu₂²/r = Beu₂, де r - радіус кола, випливає, що

r = m u₂ / B e q. (3)

Враховуючи, що на повздовжню складову u₁ з боку магнітного поля не діє сила, то рух електрона складається з рівномірного прямолінійного руху вздовж поля із швидкістю u₁ і рівномірного обертання навколо поля зі швидкістю u₂. Ясно, що траєкторія руху електрона буде являти собою гвинтову лінію. Час одного оберта навколо поля, тобто період обертання, T = 2π r / u₂, що з урахуванням (3) дає

T = 2π m / (B e). (4)

На співвідношенні (4) і грунтується метод визначення відношення e/m для електронів, який складається ось із чого. Електрони, що випускаються катодом К, проходять через отвір в аноді А. Між катодом і анодом прикладається прискорююча напруга U. Отже, із “електронної гармати” вилітає пучок електронів, швидкість яких визначається співвідношенням

m u² / 2 = e U (5)

За анодом електрони рухаються в просторі, вільному від електричного поля, і попадають на люмінесцентний екран. На трубку надягається довга котушка (соленоїд), що створює всередині трубки однорідне магнітне поле з ідукцією

B = μ₀ μ n I, (6)

де μ₀ - 4π^.10^-7 Гн/м – магнітна стала; μ - відносна магнітна проникність; n - число витків на одиницю довжини соленоїда; I - сила струму в соленоїді.

Електрони, що вилетіли за межі аноду під невеликим кутом до магнітного поля, рухаються по циліндричних спіралях. За час одного оберту Т(4) електрони вздовж поля пролітають відрізок

l = u₁ T = 2π m u₁ /(B e). (7)

Це означає, що електрони, вилітаючи із катода під деяким кутом α, знову перетинають вісь пучка в точках на відстанях l; 2l; 3l і т.д. від анода. В цих точках відбувається фокусування електронного пучка (рис.2). Отже, якщо монотонно змінювати

Рис. 2

магнітне поле або швидкість електронів, то спочатку розмита пляма на екрані буде періодично стягатися в малу пляму. Якщо відстань L між анодом А і екраном дорівнює l, то електрони пучка по завершенню одного оберту зустрінуться на екрані. При L = 2l електрони зустрінуться на екрані після двох обертів і т.д. Отже, умовою фокусування пучка на екрані є рівність L = kl, де k - ціле число з ряду: 1, 2, 3 і т.д.

Важаючи кути α малими (cos α ≈ 1), із співвідношень (5) – (7) одержуємо

e / m = 2U 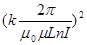. (8)

Вимірюючи значення U і I, при яких відбувається фокусування пучка на екрані, за формулою (8) обчислюють відношення e/m.

Порядок виконання роботи:

1. Вивчіть принципову схему установки (рис. 3). Схему живлення трубки,

вольтметр на 1000 В і потенціометр плавного регулювання змонтовано в окремому корпусі.

2. Під’єднайте живлення до соленоїда згідно зі схемою.

3. Після перевірки схеми викладачем ввімкніть в мережу змінного струму обидва випрямляча і встановіть потенціометром R₁ напругу 1000 В між катодом і анодом трубки. Дайте трубці прогрітися на протязі 2-3 хвилин.

4. Повільно збільшуючи силу струму в соленоїді, добивайтеся першого фокусування електронного пучка на екрані трубки, запишіть відповідне значення струму.

5. Визначте силу струму , що відповідає другому і третьому фокусуванню.

6. За формулою (8) розрахуйте величину питомого заряду електрона за результатами трьох вимірів та оцініть похибки вимірювань.

Результати вимірювань і розрахунків занесіть до таблиці:

k	n	L	U	I	e / m	Δ(e / m)2
Середні значення

Дайте відповіді на запитання:

1.Маса частинки залежить від швидкості її руху у відповідності зі спеціальною теорією відносності за формулою m = m₀/ 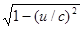. Чи принципово можна за допомогою методу даної роботи дослідити цю залежність?

2. Чим принципово відрізняються дії магнітного та електричного полів на рухому заряджену частинку?

3. Знайдіть відношення e/m за табличними даними і поясніть його відміну від знайденого у Ваших дослідах.

Лабораторна робота № 35.

Визначення ємності конденсатора за допомогою змінного струму.

Прилади та приладдя: досліджувані конденсатори, еталонний конденсатор, реостат на 3500 Ом, міліамперметр на 500 – 1000 мА, вольтметр на 300 В, вимикач, перемикач.

Мета роботи: засвоїти один із методів вимірювання ємності за допомогою змінного струму.

Коротка теорія і методика вимірювань

Змінну напругу синусоїдальної форми можна подати у вигляді

U = U₀ cos (ωt), (1)

де U₀ - амплітуда напруги; ω = 2πν - циклічна частота; ν - частота змінної напруги. Якщо напругу (1) подати в коло, що складається із послідовно ввімнених опору R, ємності С та індуктивності L, то в колі виникне змінний струм

I = I₀ cos ( ωt + φ ) (2)

Амплітуда струму I₀, що залежить від паpаметрів електричного кола і частоти ν, виражається співвідношенням

I₀ = U₀ /Z, (3)

яке подібне закону Ома для постійного струму I=U/R, якщо вважати, що величина Z - імпеданс кола - відіграє роль опору кола змінного струму. Відповідні міркування призводять до такого співвідношення для імпедансу:

Z = 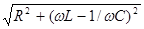. (4)

Імпеданс узвичаємо розглядати як векторну силу двох опорів - активного R і реактивного X:

X = ωL – 1 / ωC (5)

При проходженні струму по активному опорові електрична енергія перетворюється в енергію теплового руху згідно з законом Джоуля-Ленца:

dQ = I² R dt. (6)

На реактивному опорі теплові ефекти не виникають, але відбувається перетворення електричної енергії джерела струму в енергію електричного поля конденсатора і енергію магнітного поля індуктивності. Наявність реактивного опору в колі змінного струму призводить до зсуву φ фази струму відносно фази напруги ωt. Величини, що визначають реактивні опори

R_L = ωl; R_C =1 / ωC (7)

мають розмірність опору і тому називаються відповідно індуктивним і ємнісним опорами кола.

В даній роботі визначається ємність конденсатора при застосуванні змінної напруги мережі міської напруги з частотою υ=50 Гц. З цією метою коло збирається так, щоб в ньому можна було знехтувати активним і інуктивним опорами порівняно з ємнісним. Покладаючи R=0, L=0 в (4) і застовуючи (3) , перепишемо (2) у вигляді

I = U₀ ω C cos( ωt + φ ) (8)

Прилади, що вимірюють змінний струм, проградуйовані в значеннях ефективних величин: ефективна сила струму, яку показує амперметр, дорівнює I = I₀/ 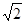, ефективна напруга - U = U₀/ 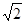. Крім того, показання приладу звичайно не залежить від зсуву фаз φ. Якщо за допомогою приладів для двох різних ємностей одержані результати I = ω C U та I₁ = ω C₁ U₁, з відношення I / I₁ маємо

C = C₁ I U₁ / ( I₁ U) (9)

Якщо відома еталонна ємність С₁ та виміряні інші величини правої частини (9), то із (9) можна знайти шукану С.

В даній роботі співвідношення (9) є розрахунковим.

Рис.1.

Порядок виконання роботи:

1.Зберемо коло змінного струму згідно зі схемою (рис.1) .

2. Перемикачем П ввімкніть у вимірювальний контур еталонний конденсатор. Після перевірки кола викладачем подайте в коло напругу вимикачем К, повзунком реостата підберіть напругу U₁ ≈ 100-150В і виміряйте струм I₁. Змінючи напругу приблизно на 30В вверх-вниз, виконайте вимірювання ще двічі. Значення І₁ та U₁ занесіть до поданої нижче таблиці.

3. Вімкніть до вимірювального контура один з досліджуваних конденсаторів С і повторіть дії пункта 2, записуючи тричі значення U та I .

4. Обчисліть три значення ємності досліджуваного конденсатора С за формулою (9) і визначте похибки вимірювань.

№	C1	U1	I1	U	I	C	(ΔC)2

Дайте відповіді на запитання:

1. Як змінюється сила струму в колі при зміні ємності?

2. Як можна спростити метод вимірювання ємностей, що вивчається?

3. Яка різниця існує між активним і реактивним опорами ?

4. В чому полягає систематична похибка при вимірюваннях за схемою (рис.1)?

Лабораторна робота № 36.

Дослідження індуктивності котушки за допомогою змінного струму.

Прилади та приладдя: досліджувана котушка з залізним осердям до неї, реостат на 1000Ом, амперметр з границями вимірювань до 15В, батарея акумуляторів, трансформатор 220-12 В, перемикач.

Мета роботи: засвоїти один із методів вимірювання індуктивності.

Коротка теорія та методика вимірювань

Змінну напругу синусоїдальної форми можна подати у вигляді виразу:

U = U₀ cos ( ωt ), (1)

де U₀ - амплітуда напруги, ω = 2πυ - циклічна частота; υ - частота змінної напруги.

Якщо напругу (1) подати в коло, що складається із послідовно ввімкнених опору R, ємності С та індуктивності L, то в ньому піде змінний струм

I = I₀ cos ( ωt + φ ), (2)

де I₀ - амплітуда струму, що залежить від параметрів електричного кола і частоти і виражається співвідношенням:

I₀ = U₀ / Z, (3)

яке подібне до закону Ома для постійного струму I=U/R, якщо вважати, що величина Z - імпеданс кола - відіграє роль опору кола змінному струму. Відповідні міркування призводять до такого співвідношення для імпедансу:

Z = 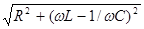. (4)

Імпеданс узвичаємо розглядати як векторну силу двох опорів - активного R і реактивного X:

X = ωL – 1 / (ωC). (5)

При проходженні струму по активному опорові електрична енергія перетворюється в енергію теплового руху згідно із законом Джоуля-Ленца

dQ = I² R dt. (6)

На реактивному опорі теплові ефекти не виникають, а відбувається перетворення електричної енергії джерела струму в енергію електричного поля конденсатора і енергію магнітного поля індуктивності. Наявність реактивного опору в колі змінного струму призводить до зсуву фази φ струму відносно фази напруги ωt. Величини, що визначають реактивний опір

X_L = ωL; X_C =1 / ωC (7)

мають розмірність опору, і тому називаються відповідно індуктивним і ємнісним опорами кола.

Для вимірювання індуктивності котушки (коефіцієнта самоіндукції) збирають коло у такий спосіб, щоб при вимірюваннях можна було знехтувати ємнісним опором. При X_C =1/(ωC) = 0 з ( 4 ) одержуемо

Z = 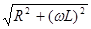. (8)

Активний опір R котушки можна знайти за законом Ома, пропускаючи через котушку постійний струм I при відомій напрузі U.

R = U / I. (9)

Прилади, що реєструють змінний струм, проградуйовані в значеннях ефективних величин: ефективна сила струму, котру реєструє амперметр, дорівнює i = I₀/ 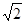, ефективна напруга u = U₀ / 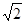. Крім того, показання приладу звичайно не залежить від зсуву фаз φ. Якщо пропускати через котушку вимірюваний змінний струм I та вимірювати напругу U на котушці , то за ( 3 ) можна визначить імпеденс котушки

Z = u / i (10)

При відомих активному опорові R і імпедансі Z за (8) обчислюють шукану індуктивність L

L = 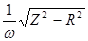. (11)

Завдання 1.

1. Зберіть коло за схемою (рис.1). Трансформатор в розетку мережі не вмикайте!

2. Після перевірки кола викладачем ввімкніть джерело постійного струму перемикачем П. Користуючись реостатом, подайте на клеми К вимірювального контура напруги, при яких струм I через котушку дорівнює 0,5; 0,7; 0,9A. Запишіть відповідні значення постійної напруги U₁, U₂, U₃.

3. За формулою (9) обчисліть R₁, R₂, R₃.

4. Повторіть дії пунктів 2-3, вставивши в котушку осердя, і впевніться, що постійний струм не впливає на результати визначення R. Вийміть осердя.

5. Ввімкніть в мережу первинну обмотку трансформатора і перемикачем П подайте змінну напругу на котушку.

6. За допомогою реостата встановіть три різні значення змінного струму в котушці, запишіть відповідні напруги .

7. За формулою (10) знайдіть три значення імедансу Z, визначте за (11) індуктивність котушки при ω = 2π υ ≈ 314 c ^-1 (υ = 50 Гц ). Зробіть оцінку похибок вимірювань.

Результати вимірювань і розрахунків подайте в таблиці:

№	I	U	R	i	u	Z	L	(ΔL)2
Середні значення

Завдання 2.

Вставте в котушку залізне осердя і виконайте дії пп. 2-7.

Дайте відповіді на запитання:

1.Які причини існування індуктивного опору?

2. Що може бути причиною похибок при вимірюванні за схемою (рис.1)?

3. Чому збільшується індуктивність при наявності осердя ?

Лабораторна робота № 37.

Дослідження електромагнітних хвиль за допомогою двохпровідної лінії.

Прилади та приладдя: генератор УКХ з випрямлячем для живлення від мережі змінного струму. Двопровідна лінія з індуктивним зв’язком, контактний місток з індикатором (лампочка розжарення), два контактних містки без індикаторів.

Мета роботи: засвоїти один із методів дослідження електромагнітних хвиль.

Коротка теорія та метод вимірювань

Розроблена Максвеллом в 19-му віці теорія єдиного електромагнітного поля сьогодні є теоретичною оновою радіотехніки. Згідно з теорією Максвелла змінне електричне поле спричинює до змінного магнітного поля, а змінне магнітне поле в свою чергу спричинює до змінного електричного поля. Ці вторинні змінні поля мають вихровий характер: силові линії змінного первинного поля концентрично

охоплені силовими лініями вторинного поля. Деякі уявлення про характер змінного електромагнітного поля може дати рис.1, що є ніби миттєвим знімком поля. Горизонтальні кола Н зображують вторинні магнітні поля, а вертикальні кола Е - вторинні електричні поля.

Рис.1 Рис.2

Будучи спочатку зв’язаними з зарядами і струмами; змінні електричні і магнітні поля можуть потім існувати незалежно від зарядів і струмів (відокремлюватись від них ) і, породжуючи один одного, поширюватися в просторі зі швидкістю:

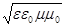v = 1 / (1)

або, якщо підставити числові значення і розмірності електричної ε₀ і магнітної сталих μ₀

v = c / 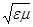, (2)

де ε і μ - відносні діелектрична та магнітна проникність середовища. Згідно з формулою (2), у вакуумі електромагнітні поля поширюються зі швидкістю v = c = 3^.10⁸ м/с, що відповідає швидкості світла у вакуумі (ε = μ = 1).

Особливістю електромагнітного поля є те, що вектори напруженості магнітного Н і електричного Е полів здійснюють коливання в однакових фазах у взаємно перпендикулярних площинах перпендикулярно променеві. Напрямок векторів Е, Н і швидкості v пов’язані між собою правилом буравчика: якщо дивитися вздовж швидкості v, то поворот від Е до Н по найкоротшому шляху спостерігається по годинниковій стрілці. Отже, електромагнітне поле поширюється у вигляді поперечної хвилі, що складається з двох співпадаючих за фазами хвиль – хвилі напруженості електричного поля і хвилі напруженості магнітного поля (Рис.2). Довжина хвилі λ, період Т, частота υ і швидкість v електромагнітної хвилі пов’язані відомим співвідношенням:

λ = v T = v / υ. (3)

Джерелами електромагнітних хвиль бувають змінні струми, тобто електричні заряди, що нерівномірно рухаються. В радіотехніці електромагнітні хвилі створюються з допомогою спеціальних пристроїв – генераторів електромагнітних коливань, основною частиною яких є коливальний контур Томсона, що складається з конденсатора С та індуктивності L (рис.3,а). Як відомо, процес електромагнітних коливань у такому контурі полягає в періодичному перетворенні енергії електричного поля зарядженого конденсатора в енергію магнітного поля котушки індуктивності, і навпаки. Коливальний контур характеризується єдиною власною частотою

υ = 1/ 2π 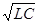. (4)

Відомо, що в системі множини пов’язаних матеріальних точок (гумовий шнур, струна) коливальний рух може поширюватись у вигляді механічної хвилі. Аналогічно цьому в системі, що складається з множини пов’язаних між собою контурів, поширення коливань являє собою електромагнітну хвилю. Прикладом такої системи є двохпровідна лінія, в якій індуктивність і ємність розподілені безперервно по всій довжині лінії. Процес розповсюдження електромагнітної хвилі у двохпровідній лінії принципово не відрізняється від розглянутого раніше випадку для однорідного середовища. Різниця є лише в тому, що змінне електричне поле призведе до виникнення в проводах струмів провідності (рис.3,б), і тому воно зосереджено між проводами. У відсутність проводів силові линії поля мали б ділянки, помічені на рисунку пунктиром. Проводи виготовлені з провідного матеріалу, тому напруженість електричного поля в них надто мала і пунктирних ділянок силових ліній в них немає.

На практиці завжди мають справу з короткими лініями, на довжині яких вкладається порівняно невелике число довжин хвиль. В цих випадках суттєву роль відіграє відбиття електромагнітних хвиль від кінців лінії. Відбиті хвилі складаються з первинною хвилею, в результаті чого виникають стоячі електромагнітні хвилі.

Розглянемо головні особливості стоячої хвилі. Для цього введемо координатну вісь Ох, спрямовану вздовж двохпровідної лінії (рис.4, а), і припустимо, що коливання первинної хвилі в довільній точці можна подати так:

E = E₀ sin [ ω( t – x/v) ]. (5)

Важаючи, що хвиля відбивається повністю, коливання відбитої хвилі в тій точці подано у вигляді

E₂ = E₀ sin [ ω( t + x/v) - φ ]. (6)

Знак “+” біля доданку x/v в (6) вказує на рух цієї хвилі в негативному напрямку осі Ох. Величину φ - це запізнення за фазою коливань поля відбитої хвилі порівняно з коливаннями первинної хвилі в тій же точці. Це запізнення зумовлено двома причинами. По-перше, до повернення в дану точку хвиля повинна пройти деякий шлях. По-друге, при відбитті можлива зміна фази. Складаючись, обидві хвилі дають результуюче поле Е = Е₁ +Е₂, Виконавши звичайні тригонометричні перетворення і врахувавши (5) та (6 ), одержимо

Е = 2 Е₀ cos ( ωx/v – φ / 2 ) sin ( ωt – φ / 2 ). (7)

Це рівняння показує, що в кожній точці лінії відбувається гармонічне коливання з частотою первинної хвилі ω і однаковою початковою фазою φ /2. Амплітуда цих коливань залежить від координати точки х

Е_a = 2 Е₀ cos ( ωx/v – φ / 2 ). (8)

В певних точках Е_a має максимуми, що відповідають значенням cos(ωx/v – φ/2) =1. Ці точки називаються пучностями електричного поля. Їх координати визначаються умовою

ωx/v – φ /2 = 0, π, 2π, …, nπ. (9)

Відстань Δx між двома сусідніми пучностями можна визначити за різницею сусідніх аргументів косинуса, заданих співвідношенням (9): ωΔx/v = π або, враховуючи v = λ / υ i ω = 2πυ

Δх = λ / 2. (10)

В інших точках двохпровідної лінії, що звуться вузлами, амплітуда Е мінімальна (дорівнює нулю). Міркування, аналогічні попереднім, приводять, також до умови (10), тобто відстань між вузлами електричного поля дорівнює половині довжини хвилі.

Рис. 4.б пояснює характер коливань поля стоячої електромагнітної хвилі. На ньому вздовж горизонталі відкладені координати х лінії, а по вертикалі - амплітуда коливань Е_a. В усіх точках між сусідніми вузлами (0-1, 1-2, і т.д.) коливання відбувається з однаковою початковою фазою, так що Е в усіх точках одначасно досягає максимуму і одночасно перетворюється в нуль у відповідності з (7). Проте при переході через вузол cos( ωx/v – φ /2) змінює знак, що відповідає зміні фази коливань на π.

Рис.3

Розглянемо тепер магнітне поле. Як відомо, в електромагнітній хвилі, що поширюється, коливання електричного і магнітного полів відбувається в одній фазі. В стоячій хвилі це вже не має місця, тому що між коливаннями Е і Н з’являється різниця фаз у зв’язку з відбиванням хвилі від кінця лінії. В тому, що при відбиванні від кінця лінії має змінюватися на протилежну фаза одного із полів, можна впевнитися при простому міркуванні. При оберненні швидкості для дотримання правила правого буравчика маємо змінити напрямок Е або Н. Якщо лінія замкнута провідним містком, то напруга між кінцями лінії дорівнює нулю, і на кінці лінії буде розміщений вузол електричного поля. Це значить, що при відбиванні електричної хвилі від замкнутого кінця лінії відбувається зміна фази електричного поля на протилежну. Амплітуда ж струму в провідному містку завжди максимальна, а отже, максимальне навколо нього магнітне поле, тобто при відбитті від замкнутого кінця лінії магнітне поле не змінює фазу коливань.

Таким чином, в стоячій електромагнітній хвилі вузли електричного поля співпадають з пучностями магнітного поля, і навпаки. Для виникнення в двопровідній лінії стоячої електромагнітної хвилі необхідно, щоб на довжині лінії вкладалось ціле число півхвиль

L = k λ / 2 , k = 1, 2, 3, … . (11)

На рис. 5 зображена стояча хвиля, що відповідає k = 3. Якщо умова (11) не виконується, то при відбиванні стійкої стоячої електромагнітної хвилі не одержується.

Рис. 4 Рис. 5

Створюючи у двохпровідної лінії режим стоячої хвилі підбором довжини за розміщенням вузлів і пучностей Н або Е (за максимальним значенням І або U), можна визначити довжину хвилі, а при відомій частоті генератора – і швидкість її поширення.

Установка, що застосовується в даній роботі (рис.5), складається із генератора, індуктивно зв’язаного витком К з двохпровідною лінією. Виток зв’язку К разом з тим є індуктивністю контура генератора. Ємністю є міжелектродна ємність ламп генератора. У такий спосіб індуктивність і ємність в колі генератора зведені до мінімуму. Як випливає з (4), це дає можливість одержати коливання ультрависокої частоти (УВЧ) .Індикатором в даній установці є лампочка розжарення малого опору. Це дозволяє вважати, що накладанням індикатора закорочують лінію, тобто в цьому місці відбувається зміна фази електричного поля на π з великою мірою точності. Для одержання стоячих хвиль в проводах закороченої лінії маємо на них вкласти ціле число півхвиль, тому система має бути налагоджена. Це робиться спостеріганням яскравості свічення індикатора при переміщенні його вздовж проводів. Найбільша яскравість свічення лампочки індикатора в будь-якому місці вказує на те, що в проміжку між індикатором і початком лінії (витком зв’язку К) вклалось ціле число півхвиль і встановився режим стоячої хвилі з пучностями струму. На лампочці ж все-таки падає деяка напруга, тому вузол напруженості тут не виникакє.

Якщо поблизу індикатора довільно розмістити контактний місток, то режим стоячої хвилі порушиться (лампочка погасне), але при зсуванні містка від індикатора на λ /2 режим стоячої хвилі знову відновиться, і лампочка загориться. На цьому грунтується метод вимірювання довжини хвилі.

Порядок виконання роботи:

1. Зберіть схему, під’єднавши до генератора блок живлення. Без перевірки схеми викладачем випрямляч в мережу не вмикайте!

2. Наладнайте схему. Для цього на двохпровідну лінію помістить лампочку-індикатор і, зсуваючи її, знайдіть місце найбільш яскравого свічення лампочки.

3. Залишивши лампочку в місці найбільш яскравого свічення, помістіть поблизу неї контактний місток (без лампочки) і переміщуйте його вздовж лінії доти, поки лампа-індикатор знову загориться яскраво. Аналогічно проробіть і з другим містком, помістивши його з того ж боку індикаторної лампи.

4. Виміряйте відстані L₁, L₂, L₃ ( між індикаторною лампою, першим і другим містками, а також між перекидними містками).

5. Визначити відстані між сусідніми пучностями за формулою:

Lср.= ( L₃ + L₂ + L₁/2 ) / 3.

Знаючи, що довжина електромагнітної хвилі дорівнює λ=2Lср., визначте довжину електромагнітної хвилі.