Квантовые числа, определяющие состояния электронов в атоме, их физический смысл и возможные значения
Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.
1. Главное квантовое число 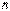 . Это квантовое число принимает значения
. Это квантовое число принимает значения
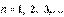
и определяет полную энергию электрона в любом квантовом состоянии
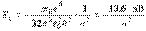 |
Можно отметить, что эти значения энергии являются собственными значениями гамильтониана. Поэтому в связанном состоянии электрон в атоме водорода имеет дискретный энергетический спектр, лежащий в области отрицательных значений и имеющий точку сгущения 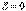 .
.
2. Орбитальное (азимутальное) квантовое число 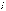 . В квантовых состояниях с заданным значением главного квантового числа
. В квантовых состояниях с заданным значением главного квантового числа 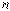 азимутальное квантовое число может иметь следующие значения:
азимутальное квантовое число может иметь следующие значения:
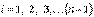 .
.
Стационарные волновые функции 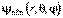 , описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии
, описывающие различные квантовые состояния атома, являются собственными функциями не только оператора полной энергии 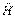 , но и оператора квадрата момента импульса
, но и оператора квадрата момента импульса 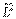 , причем:
, причем: 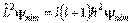 .
.
Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:
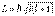 . . |
3. Магнитное квантовое число 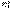 . В квантовом состоянии с заданным значением орбитального квантового числа
. В квантовом состоянии с заданным значением орбитального квантового числа 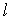 , магнитное квантовое число может принимать
, магнитное квантовое число может принимать 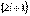 различных значений из ряда
различных значений из ряда
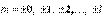 . Физический смысл магнитного квантового числа вытекает из того, что волновая функция
. Физический смысл магнитного квантового числа вытекает из того, что волновая функция 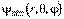 , описывающая квантовое состояние электрона в атоме водорода, является собственной функцией оператора проекции момента импульса
, описывающая квантовое состояние электрона в атоме водорода, является собственной функцией оператора проекции момента импульса 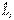 , причем
, причем 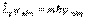 .
.
Поэтому, из общих положений квантовой механики следует, что проекция момента импульса электрона на выделенное в пространстве направление 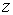 может иметь только определенные значения, равные
может иметь только определенные значения, равные
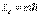 . . | (5.41) |
Направление 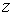 в пространстве обычно выделяется внешним полем (например, магнитным или электрическим), в котором находится атом.
в пространстве обычно выделяется внешним полем (например, магнитным или электрическим), в котором находится атом.
Так как формула (5.41) квантования проекции механического момента соответствует вполне определенным направлениям ориентации в пространстве вектора 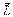 (рис. 5.9), то эту формулу называют обычно формулой пространственного квантования.
(рис. 5.9), то эту формулу называют обычно формулой пространственного квантования.
С точки зрения классического представления об электронной орбите, с учетом перпендикулярности вектора 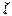 к плоскости орбиты, соотношение (5.41) определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.
к плоскости орбиты, соотношение (5.41) определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.
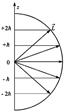 |
| Рис. 5.9. |
Отмеченная выше связь механического и магнитного моментов атома позволяет с учетом (5.41) записать также возможные значения проекции магнитного момента атома на выделенное направление 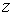 :
:
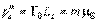 , , |
зависящие от значения магнитного квантового числа 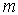 .
.
