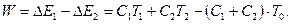Задача 3. Довести співвідношення
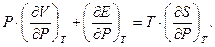
Розв’язання. Нехай незалежними змінними будуть параметри 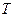 і
і 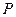 . Тоді
. Тоді 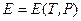 та
та
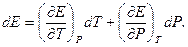 (1)
(1)
З іншого боку, основне рівняння термодинаміки (3.13) можна записати у вигляді
 . (2)
. (2)
Оскільки ми вважаємо: 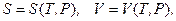 розписуючи повні диференціали
розписуючи повні диференціали 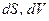 і підставляючи їх в (2), знайдемо:
і підставляючи їх в (2), знайдемо:
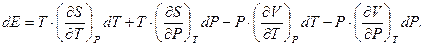 (3)
(3)
Порівнюючи коефіцієнти в рівностях (1) і (3) при 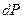 , отримуємо потрібний результат.
, отримуємо потрібний результат.
Задача 4. Показати, що теплоємність 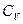 газу Ван-дер-Ваальса не залежить від об’єму.
газу Ван-дер-Ваальса не залежить від об’єму.
Розв’язання. За визначенням маємо
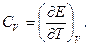 (1)
(1)
Треба довести
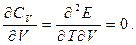
Розглянемо співвідношення (3.19):
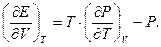
Диференціюючи його за 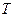 при V = const, отримаємо
при V = const, отримаємо
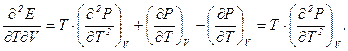 (2)
(2)
Оскільки для 1 моля газу Ван-дер-Ваальса 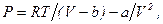 то для нього
то для нього
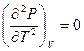 .
.
Підставляючи цей результат в (2), знаходимо
 ,
,
тому й 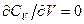 , що й потрібно було довести.
, що й потрібно було довести.
Задача 5. Визначити рівняння адіабати газу Ван-дер-Ваальса в змінних 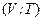 .
.
Розв’язання. Диференціальне рівняння адіабати (2.13) можна записати як
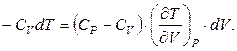 (1)
(1)
Використовуючи формулу (3.21) для 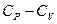 , перепишемо (1) у вигляді
, перепишемо (1) у вигляді

або (після очевидних скорочень)
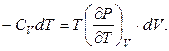 (2)
(2)
З рівняння Ван-дер-Ваальса для 1 моля маємо
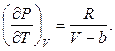 (3)
(3)
Тоді з урахуванням (3) і після розділення змінних рівняння (2) набере вигляду
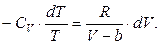 (4)
(4)
Інтегруючи (4), після алгебраїчних перетворень знаходимо
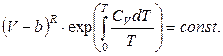
Якщо вважати 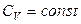 , результат спрощується і рівняння адіабати набирає вигляду
, результат спрощується і рівняння адіабати набирає вигляду
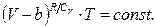
Відзначимо, що в наближенні, коли 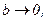 це рівняння перетворюється на рівняння адіабати ідеального газу.
це рівняння перетворюється на рівняння адіабати ідеального газу.
Задача 6. Яку роботу 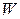 здійснює один моль газу Ван-дер-Ваальса при адіабатному процесі, коли його об’єм міняється від
здійснює один моль газу Ван-дер-Ваальса при адіабатному процесі, коли його об’єм міняється від  до
до 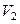 ? Початкова температура дорівнює
? Початкова температура дорівнює 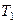 . Вважати
. Вважати 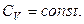
Розв’язання. З першого начала термодинаміки для адіабатного процесу 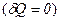 маємо
маємо  або в розгорненому вигляді:
або в розгорненому вигляді:
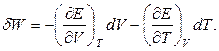 (1)
(1)
Беручи до уваги результати задачі 2 цієї глави, елементарну роботу  , що здійснюється одним молем газу Ван-дер-Ваальса, можна записати як
, що здійснюється одним молем газу Ван-дер-Ваальса, можна записати як
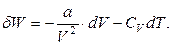 (2)
(2)
Інтегруючи (2), знаходимо шукану роботу
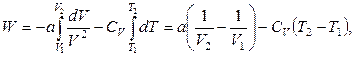
де 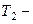 кінцева температура. Значення
кінцева температура. Значення 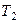 знайдемо з рівняння адіабати газу Ван-дер-Ваальса (див. попередню задачу), згідно з яким
знайдемо з рівняння адіабати газу Ван-дер-Ваальса (див. попередню задачу), згідно з яким
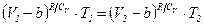 ,
,
звідки

Задача 7. Два ідеальних гази з фіксованими об’ємами і постійними теплоємностями  і
і 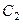 знаходяться в початкових станах з температурами
знаходяться в початкових станах з температурами 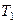 і
і 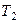
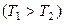 відповідно. Вони адіабатно ізольовані один від одного. Яку роботу
відповідно. Вони адіабатно ізольовані один від одного. Яку роботу 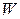 можна утворити, використовуючи перший газ у ролі джерела тепла, а другий у ролі поглинача до тих пір, доки не встановиться їх однакова температура
можна утворити, використовуючи перший газ у ролі джерела тепла, а другий у ролі поглинача до тих пір, доки не встановиться їх однакова температура 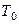 ? Знайти вираз для
? Знайти вираз для 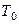 .
.
Розв’язання. Спочатку визначимо вираз для 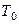 . Через адіабатну ізольованість газів зміна їх ентропії
. Через адіабатну ізольованість газів зміна їх ентропії 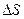 в цілому (при рівноважних процесах утворення шуканої роботи) дорівнюватиме нулю:
в цілому (при рівноважних процесах утворення шуканої роботи) дорівнюватиме нулю:
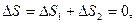 (1)
(1)
де  і
і 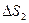 – зміна ентропій першого і другого газів відповідно від свого початкового стану до стану з температурою
– зміна ентропій першого і другого газів відповідно від свого початкового стану до стану з температурою 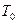 . З формули (3.4) і з урахуванням
. З формули (3.4) і з урахуванням  знаходимо
знаходимо
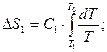
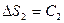
 (2)
(2)
Підставляючи (2) в (1) і інтегруючи, отримаємо

звідки

Потрібну роботу 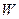 можна отримати з закону збереження енергії як повне зменшення внутрішньої енергії газів. Дійсно, оскільки
можна отримати з закону збереження енергії як повне зменшення внутрішньої енергії газів. Дійсно, оскільки 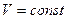 , внутрішня енергія
, внутрішня енергія 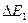 , віддана першим газом у вигляді теплоти, дорівнюватиме
, віддана першим газом у вигляді теплоти, дорівнюватиме
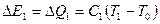 ,
,
а внутрішня енергія 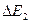 , отримана другим газом у вигляді теплоти, дорівнюватиме
, отримана другим газом у вигляді теплоти, дорівнюватиме
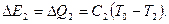
Отже,