Электромагнитные колебания. Переменный ток.
Общие методические указания
При решении и оформлении задач необходимо соблюдать следующие требования:
1. Записать краткое условие задачи, выразить все известные величины в одной и той же системе единиц (как правило, в СИ). При необходимости ввести дополнительные постоянные физические величины.
2. Решение задач следует сопровождать краткими, но исчерпывающими объяснениями. При необходимости дать чертеж или график.
3. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. Произвести вычисления по расчетной формуле с соблюдением правил приближенных вычислений.
Результаты контроля аудиторной и самостоятельной работы студентов на практических занятиях учитываются лектором при приеме экзаменов и дифференцированных зачетов.
Электростатика
Основные формулы и законы
· Закон Кулона
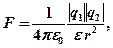
где 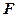 – модуль силы взаимодействия двух точечных зарядов
– модуль силы взаимодействия двух точечных зарядов 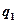 и
и 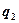 ;
; 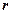 – расстояние между зарядами;
– расстояние между зарядами; 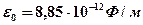 - электрическая постоянная,
- электрическая постоянная, 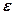 -диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума
-диэлектрическая проницаемость среды, в которой находятся заряды (для вакуума 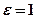 )
)
· Напряженность и потенциал электростатического поля
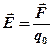 ;
; 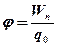 , или
, или 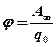 ,
,
где 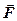 – сила, действующая на точечный положительный заряд
– сила, действующая на точечный положительный заряд 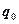 , помещенный в данную точку поля;
, помещенный в данную точку поля; 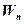 – потенциальная энергия заряда
– потенциальная энергия заряда 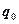 ;
; 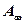 – работа по перемещению заряда
– работа по перемещению заряда 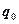 из данной точки поля в бесконечность.
из данной точки поля в бесконечность.
· Напряженность и потенциал электростатического поля, создаваемого точечным зарядом 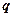 на расстоянии
на расстоянии 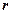 от него
от него
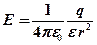 ;
; 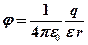 .
.
· Поток вектора напряженности через площадку 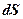
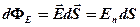 ,
,
где 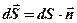 – вектор, модуль которого равен
– вектор, модуль которого равен 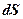 , а направление совпадает с нормалью
, а направление совпадает с нормалью 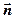 к площадке;
к площадке; 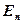 – составляющая вектора
– составляющая вектора 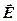 по направлению нормали
по направлению нормали 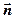 к площадке.
к площадке.
· Поток вектора напряженности через произвольную поверхность 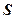
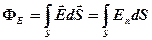 .
.
· Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции (наложения) электростатических полей)
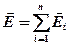 ;
; 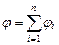 ,
,
где 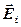 ,
, 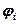 – соответственно напряженность и потенциал поля, создаваемого зарядом
– соответственно напряженность и потенциал поля, создаваемого зарядом 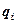 ,
, 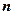 – число зарядов, создающих поле.
– число зарядов, создающих поле.
· Связь между напряженностью и потенциалом электростатического поля
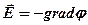 , или
, или 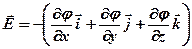 ,
,
где 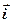 ,
, 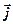 ,
, 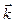 – единичные векторы координатных осей.
– единичные векторы координатных осей.
· В случае поля, обладающего центральной или осевой симметрией,
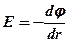 .
.
· Для однородного поля (поля плоского конденсатора)
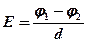 ,
,
где 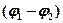 - разность потенциалов между пластинами конденсатора,
- разность потенциалов между пластинами конденсатора, 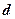 - расстояние между ними.
- расстояние между ними.
· Электрический момент диполя (дипольный момент)
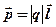 ,
,
где 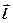 – плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).
– плечо диполя (векторная величина, направленная от отрицательного заряда к положительному).
· Линейная, поверхностная и объемная плотность зарядов, т.е. заряд, приходящийся соответственно на единицу длины, площади и объема:
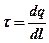 ;
; 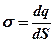 ;
; 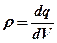 .
.
· Теорема Гаусса для электростатического поля в вакууме
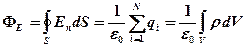 ,
,
где 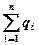 – алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности
– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности 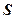 ;
; 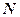 – число зарядов;
– число зарядов; 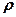 – объемная плотность зарядов.
– объемная плотность зарядов.
· Напряженность поля, создаваемая равномерно заряженной бесконечной плоскостью,
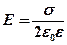 .
.
· Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом 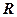 с зарядом
с зарядом 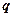 на расстоянии
на расстоянии 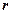 от центра сферы,
от центра сферы,
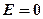 ;
; 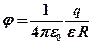 при
при 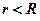 (внутри сферы);
(внутри сферы);
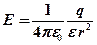 ;
; 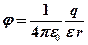 при
при 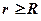 (вне сферы).
(вне сферы).
· Напряженность поля, создаваемого равномерно заряженной бесконечной цилиндрической поверхностью радиусом 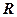 на расстоянии
на расстоянии 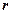 от оси цилиндра,
от оси цилиндра,
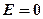 при
при 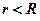 (внутри цилиндра);
(внутри цилиндра);
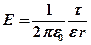 при
при 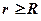 (вне цилиндра).
(вне цилиндра).
· Работа, совершаемая силами электростатического поля при перемещении заряда 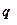 из точки 1(потенциал
из точки 1(потенциал 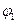 ) в точку 2 (потенциал
) в точку 2 (потенциал 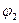 ),
),
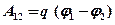 , или
, или 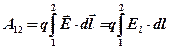 ,
,
где 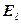 – проекция вектора
– проекция вектора 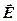 на направление элементарного перемещения
на направление элементарного перемещения 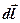 .
.
· Вектор поляризации диэлектрика
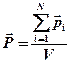 ,
,
где 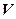 – объем диэлектрика;
– объем диэлектрика; 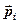 – дипольный момент
– дипольный момент 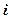 -й молекулы,
-й молекулы, 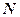 – число молекул.
– число молекул.
· Связь между вектором поляризации и напряженностью электростатического поля в той же точке внутри диэлектрика
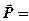 æe0
æe0 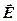 ,
,
где æ – диэлектрическая восприимчивость вещества.
· Связь диэлектрической проницаемости 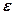 с диэлектрической восприимчивостью æ
с диэлектрической восприимчивостью æ
e = 1 + æ.
· Связь между напряженностью 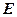 поля в диэлектрике и напряженностью
поля в диэлектрике и напряженностью 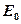 внешнего поля
внешнего поля
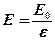 .
.
· Связь между векторами электрического смещения и напряженности электростатического поля
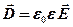 .
.
· Связь между векторами 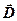 ,
, 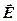 и
и 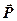
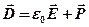 .
.
· Теорема Гаусса для электростатического поля в диэлектрике
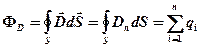 ,
,
где 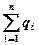 – алгебраическая сумма заключенных внутри замкнутой поверхности
– алгебраическая сумма заключенных внутри замкнутой поверхности 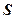 свободных электрических зарядов;
свободных электрических зарядов; 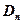 – составляющая вектора
– составляющая вектора 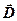 по направлению нормали
по направлению нормали 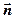 к площадке
к площадке 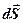 ;
; 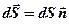 – вектор, модуль которого равен
– вектор, модуль которого равен 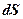 , а направление совпадает с нормалью
, а направление совпадает с нормалью 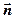 к площадке. Интегрирование ведется по всей поверхности.
к площадке. Интегрирование ведется по всей поверхности.
· Электроемкость уединенного проводника и конденсатора
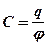 ,
, 
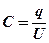 ,
,
где 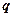 – заряд, сообщенный проводнику;
– заряд, сообщенный проводнику; 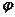 – потенциал проводника;
– потенциал проводника; 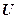 – разность потенциалов между пластинами конденсатора.
– разность потенциалов между пластинами конденсатора.
· Электроемкость плоского конденсатора
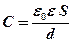 ,
,
где 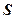 – площадь пластины конденсатора;
– площадь пластины конденсатора; 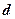 – расстояние между пластинами.
– расстояние между пластинами.
· Электроемкость батареи конденсаторов: при последовательном (а) и параллельном (б) соединениях
а) 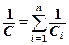 , б)
, б) 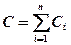 ,
,
где 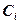 – электроемкость
– электроемкость 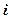 -го конденсатора;
-го конденсатора; 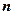 – число конденсаторов.
– число конденсаторов.
· Энергия уединенного заряженного проводника
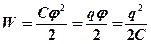 .
.
· Потенциальная энергия системы точечных зарядов
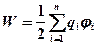 ,
,
где 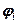 – потенциал, создаваемый в той точке, где находится заряд
– потенциал, создаваемый в той точке, где находится заряд 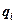 , всеми зарядами, кроме
, всеми зарядами, кроме 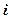 -го,
-го, 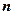 - число зарядов.
- число зарядов.
· Энергия заряженного конденсатора
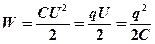 ,
,
где 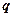 – заряд конденсатора;
– заряд конденсатора; 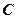 – его электроёмкость;
– его электроёмкость; 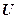 – разность потенциалов между обкладками.
– разность потенциалов между обкладками.
· Сила притяжения между двумя разноименно заряженными обкладками плоского конденсатора
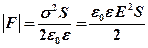 .
.
· Энергия электростатического поля плоского конденсатора
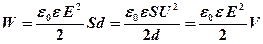 ,
,
где 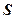 – площадь одной пластины;
– площадь одной пластины; 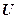 – разность потенциалов между пластинами;
– разность потенциалов между пластинами; 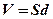 – объем области между пластинами конденсатора.
– объем области между пластинами конденсатора.
· Объемная плотность энергии электростатического поля
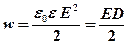 ,
,
где 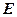 – напряжённость поля,
– напряжённость поля, 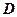 – электрическое смещение.
– электрическое смещение.
Задания
1.1.Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусами 0,1 мм уравновешивается кулоновской силой отталкивания. Определите заряд капель. Плотность воды равна 1 г/см3. [0,36 аКл].
1.2.Во сколько раз сила гравитационного взаимодействия между двумя протонами меньше силы их кулоновского отталкивания? Заряд протона численно равен заряду электрона. [в 1,25∙1038 раза].
1.3.Три одинаковых точечных заряда q1 =q2 = q3 = 2 нКл находятся в вершинах равностороннего треугольника со сторонами 10 см. Определите модуль и направление силы, действующей на один из зарядов со стороны двух других. [6,2мкН].
1.4.В вершинах равностороннего треугольника находятся одинаковые положительные заряды q = 2 нКл. Какой отрицательный заряд q1 необходимо поместить в центр треугольника, чтобы сила притяжения со стороны заряда q1 уравновесила силы отталкивания положительных зарядов? [1,15нКл].
1.5.Четыре одинаковых точечных заряда q1 =q2 = q3 = q4 = 2 нКл находятся в вершинах квадрата со стороной 10 см. Определите силу, действующую на один из зарядов со стороны трех других. [7мкН].
1.6.Два шарика одинакового радиуса и массы подвешены на двух нитях так, что их поверхности соприкасаются. После сообщения шарикам заряда 4.10-7Кл они оттолкнулись друг от друга и разошлись на угол 60˚. Найдите массу каждого шарика, если длина нити 20 см. [1,56.10-3 кг].
1.7.Два шарика массой 1 кг каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол 60˚? [7,6 мкКл].
1.8.К бесконечно заряженной плоскости с поверхностной плотностью заряда 8,85 нКл/см2 прикреплен на нити одноименно заряженный шарик с массой 1г и зарядом 2нКл. Какой угол с плоскостью образует нить, на которой висит шарик?[45˚].
1.9.С какой силой, приходящейся на единицу площади, отталкиваются две одноименно заряженные бесконечно протяженные плоскости? Поверхностная плотность заряда на каждой плоскости 2 мкКл/м2? [0,2 Н/м2].
1.10.С какой силой, приходящейся на единицу длины, отталкиваются две одноименно заряженные бесконечно длинные нити с одинаковой линейной плотностью заряда 2 мкКл/м, находящихся на расстоянии 2 см друг от друга? [3,6 Н/м].
1.11.С какой силой электрическое поле заряженной бесконечной плоскости действует на каждый метр заряженной бесконечно длинной нити, помещенной в это поле? Поверхностная плотность заряда на плоскости равна 2 мкКл/м2 и линейная плотность заряда на плоскости 2 мкКл/м. [0,2Н/м].
1.12.Тонкий прямой стержень длиной 15 см равномерно заряжен с линейной плотностью 0,10 мКл/м. На продолжении оси стержня на расстоянии 10 см от ближайшего конца находится точечный заряд 10 нКл. Определите силу взаимодействия стержня и заряда. [56 мН].
1.13.На тонком стержне длиной 20 см находится равномерно распределенный электрический заряд. На продолжении оси стержня, на расстоянии 10 см от ближнего конца, находится точечный заряд 40 нКл, который взаимодействует со стержнем с силой 6 мкН. Определите линейную плотность заряда на стержне. [2,5 нКл/м].
1.14.Два точечных заряда q1 =4 нКл и q2=-2 нКл находятся друг от друга на расстоянии 60 см. Определите напряженность поля в точке, расположенной посередине между зарядами. [0,6 кВ/м].
1.15.Чему равна напряженность поля в точке, расположенной посередине между точечными зарядами q1 = 4нКл и q2= 2 нКл? Расстояние между зарядами равно 60 см. [0,2 кВ/м].
1.16.Определите напряженность поля в точке, находящейся на прямой, соединяющей заряды q1 =10 нКл и q2=-8 нКл, на расстоянии 8 см справа от отрицательного заряда. Расстояние между зарядами равно 20 см. [10 кВ/м].
1.17.Определите напряженность поля в точке, находящейся на прямой, соединяющей заряды q1 =10 нКл и q2=-8 нКл, на расстоянии 8 см слева от отрицательного заряда. Расстояние между зарядами равно 20 см. [17,5 кВ/м].
1.18.Расстояние между двумя точечными зарядами
q1= 2 нКл и q2 = – 3 нКл, расположенными в вакууме, равно
25 см. Определите напряженность поля, создаваемого этими зарядами в точке, удаленной от первого заряда на расстояние 20 см и от второго заряда на 15 см. [1,3кВ/м].
1.19.Расстояние между одноименными одинаковыми зарядами q = 2 нКл равно 10 см. Определите напряженность поля, создаваемого этими зарядами в точке, находящейся на расстоянии 8 см от первого и 6 см от второго заряда. [5,7 кВ/м].
1.20.В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды q = 2 нКл. Определите напряженность электростатического поля: 1) в центре квадрата;
2) в середине одной из сторон квадрата. [1) 0; 2) 10,3 кВ/м].
1.21.Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно одноименными зарядами с поверхностной плотностью соответственно s1=2нКл/м2 и s2=4 нКл/м2. Определите модуль напряженности электростатического поля: 1) между плоскостями;
2) за пределами плоскостей. [1) 113 В/м; 2) 339 В/м].
1.22.Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно разноименными зарядами с поверхностной плотностью
s1 = 1 нКл/м2 и s2 =- 2 нКл/м2. Определите модуль напряженности электростатического поля: 1) между плоскостями; 2) за пределами плоскостей. [1) 169 В/м; 2) 56,5 В/м].
1.23.На металлической сфере радиусом 15 см находится заряд q = 2 нКл. Определите напряженность электростатического поля: 1) на расстоянии 10 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии 20 см от центра сферы. Постройте график зависимости напряженности поля от расстояния. [1) 0; 2) 800 В/м;
3) 450 В/м].
1.24.Кольцо радиусом 5 см из тонкой проволоки равномерно заряжено с линейной плотностью t = 14 нКл/м. Определите напряженность поля на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца. [2,83 кВ/м].
1.25.Поле создано двумя равномерно заряженными концентрическими сферами радиусами R1= 5 см и R2 = 8 см. Заряды сфер соответственно равны q1 = 2 нКл и q2 = -1 нКл. Определите напряженность электростатического поля в точках, лежащих от центра сфер на расстояниях: 1) r1 = 3 см; 2) r2 = 6 см; 3) r3 = 10 см. [1) 0; 2) 5 кВ/м; 3) 0,9 кВ/м].
1.26.Определите поток ФЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды q1 = 5 нКл и q2 = -2 нКл. [339 В×м].
1.27.Определите поток ФЕ вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды q1 = 5 нКл и q2 = 2 нКл. [790 В×м].
1.28.На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью 0,1 нКл/см2 расположена круглая пластинка. Нормаль к плоскости пластинки составляет с линиями напряженности угол 30°. Определите поток ФЕ вектора напряженности через эту пластинку, если ее радиус равен 15 см. [3,46 кВ×м].
1.29.Электростатическое поле создается положительным точечным зарядом. Определите числовое значение и направление градиента потенциала этого поля, если на расстоянии 10 см от заряда потенциал равен 100 В. [1 кВ/м, направлен к заряду].
1.30.Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью 5нКл/м2. Определите числовое значение и направление градиента потенциала этого поля. [282 В/м, направлен к плоскости].
1.31.Электростатическое поле создается бесконечной прямой нитью, заряженной равномерно с линейной плотностью 50 пКл/см. Определите числовое значение и направление градиента потенциала в точке на расстоянии 0,5 м от нити. [180 В/м, направлен к нити].
1.32.Расстояние между двумя точечными зарядами q1 = 2 нКл и q2 = -3 нКл, расположенными в вакууме, равно 20 см. Определите потенциал поля, создаваемого этими зарядами в точке, удаленной от первого заряда на расстояние 15 см и от второго заряда на 10 см. [–150В].
1.33.Электростатическое поле создается в вакууме бесконечным цилиндром радиусом 8 мм, равномерно заряженным с линейной плотностью 10 нКл/м. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях 2 мм и 7 мм от поверхности этого цилиндра. [73 В].
1.34.Металлический шар радиусом 5 см имеет заряд
q = 10 нКл. Определите потенциал электростатического поля: 1) на поверхности шара; 2) на расстоянии 2 см от его поверхности. [1) 1,8 кВ; 2) 1,29 кВ].
1.35.Тонкое кольцо радиусом 5 см из тонкой проволоки имеет равномерно распределенный заряд q = 10 нКл. Определите потенциал j электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние 10 см от центра кольца. [1) 1,8 кВ; 2) 805 В].
1.36.Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью s = 1 нКл/м2. Определите разность потенциалов между двумя точками этого поля, расположенными на расстоянии 20 и 50 см от плоскости. [16,9 В].
1.37.Электростатическое поле создается равномерно заряженной сферической поверхностью радиусом 10 см с зарядом q=15нКл. Определите разность потенциалов между двумя точками этого поля, расположенными на расстоянии 5 см и 15 см от поверхности сферы. [360 В].
1.38.Электростатическое поле создается сферой радиусом 5 см, равномерно заряженной с поверхностной плотностью
1 нКл/м2. Определите разность потенциалов между двумя точками поля, расположенными на расстоянии 10 см и 15 см от центра сферы. [0,94 В].
1.39.Электростатическое поле создается равномерно заряженным шаром радиусом 1 м и зарядом 50 нКл. Определите разность потенциалов для точек, расположенных от центра шара на расстоянии 1,5 и 2 м. [75 В].
1.40.Электростатическое поле создается шаром радиусом
8 см, равномерно заряженным с объемной плотностью 10 нКл/м3. Определите разность потенциалов между двумя точками этого поля, расположенными на расстояниях 10 и 15 см от центра шара. [0,64 В] .
1.41.Электростатическое поле создается в вакууме непроводящим шаром радиусом 10 см, равномерно заряженным с объемной плотностью 20 нКл/м3. Определите разность потенциалов между точками, расположенными внутри шара на расстоянии
2 и 8 см от его центра. [2,26 В].
1.42.Электростатическое поле создается положительно заряженной с постоянной поверхностной плотностью 10 нКл/м2 бесконечной плоскостью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния 2 см до 1 см от плоскости? [9,04.10-19 Дж].
1.43.Под действием электростатического поля равномерно заряженной бесконечной плоскости точечный заряд q=1 нКл переместился вдоль силовой линии на расстояние 1 см; при этом совершена работа 5 мкДж. Определите поверхностную плотность заряда на плоскости. [8,85 мкКл/м2].
1.44.Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью заряда 1 нКл/см. Какую скорость приобретет электрон, приблизившись к нити вдоль линии напряженности с расстояния 1,5 см до 1 см от нити? Начальная скорость электрона равна нулю.
[16 Мм/с].
1.45.Одинаковые заряды q = 100 нКл расположены в вершинах квадрата со стороной 10 см. Определите потенциальную энергию этой системы. [4,87 мДж].
1.46.Сферическая поверхность имеет равномерно распределенный заряд. Определите радиус поверхности сферы, если потенциал в центре шара равен 200 В, а в точке, лежащей от его центра на расстоянии 50 см, 40 В. [10 см].
1.47.Определите линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда q =1 нКл с расстояния 5 см до 2 см в направлении, перпендикулярном нити, равна 50 мкДж. [3,03 мКл/м].
1.48.Электростатическое поле создается положительно заряженной бесконечной нитью. Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния 1 см до расстояния5 см, изменил свою скорость от 1 до 10 Мм/с. Определите линейную плотность заряда нити. [17,8 мкКл/м].
1.49.Определите ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, чтобы его скорость возросла от 1Мм/с до 5 Мм/с. [68,3 В].
1.50.Какую ускоряющую разность потенциалов должен пройти в электрическом поле электрон, чтобы получить скорость 8 Мм/с? [182 В].
1.51.Определите ускоряющую разность потенциалов, которую должен пройти в электрическом поле электрон, обладающий скоростью 1 Мм/с, чтобы скорость его возросла в 2 раза. [8,5 В].
1.52.Определите поверхностную плотность зарядов на пластинах плоского слюдяного (e=7) конденсатора, заряженного до разности потенциалов 200 В, если расстояние между его пластинами равно 0,5мм. [24,8 мкКл/м2].
1.53.Расстояние между пластинами плоского конденсатора 5 мм. После зарядки конденсатора до разности потенциалов 500 В между пластинами конденсатора поместили стеклянную пластинку (e=7), полностью заполняющую пространство конденсатора. Определите: 1) диэлектрическую восприимчивость стекла; 2) поверхностную плотность связанных зарядов на стеклянной пластинке. [1) 6; 2) 759 нКл/м2].
1.54.Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектрика — слюдяной пластиной (e1=7) толщиной d1 = 1 мм и парафиновой пластиной (e2=2) толщиной d2 = 0,5 мм. Определите: 1) напряженности электростатических полей в слоях диэлектрика; 2) электрическое смещение, если разность потенциалов между пластинами конденсатора U = 500 В. [1) Е1= 182 кВ/м, Е2 = 637 кВ/м; 2) D = 11,3 мкКл/м2].
1.55.Расстояние между пластинами плоского конденсатора d = 5 мм, разность потенциалов U = 1,2 кВ. Определите: 1) поверхностную плотность заряда на пластинах конденсатора; 2) поверхностную плотность связанных зарядов на диэлектрике, если известно, что диэлектрическая восприимчивость диэлектрика, заполняющего пространство между пластинами, æ = 1. [1)
4,25 мкКл/м2; 2) 2,12 мкКл/м2] .
1.56.Пространство между пластинами плоского конденсатора заполнено стеклом (e = 7). Расстояние между пластинами
d = 5 мм, разность потенциалов U = 1 кВ. Определите:
1) напряженность поля в стекле; 2) поверхностную плотность заряда на пластинах конденсатора; 3) поверхностную плотность связанных зарядов на стекле.[1) 200 кВ/м; 2) 12,4 мкКл/м2;
3) 10,6мкКл/м2].
1.57.Определите расстояние между пластинами плоского конденсатора, если между ними приложена разность потенциалов U=150 В, причем площадь каждой пластины S=100 см2, ее заряд q=10 нКл. Диэлектриком является слюда (e =7). [9,29 мм].
1.58.На пластинах плоского конденсатора находится заряд 10 нКл. Площадь каждой пластины конденсатора равна 100 см2 , диэлектрик – воздух. Определите силу, с которой притягиваются пластины. Поле между пластинами считать однородным.
[565 мкН].
1.59.Разность потенциалов между пластинами плоского конденсатора U=100 В. Площадь каждой пластины S=200 см2, расстояние между пластинами d=0,5 мм, пространство между ними заполнено парафином (e =2). Определите силу притяжения пластин друг к другу. [7,08 мН].
1.60.Шар, погруженный в масло (e = 2,2), имеет поверхностную плотность заряда s=1 мкКл/м2 и потенциал j=500 В. Определите: 1) радиус шара; 2) заряд шара; 3) электрическую емкость шара; 4) энергию шара. [1) 9,74 мм; 2) 1,19 нКл; 3) 2,38 пФ; 4) 0,3 мкДж].
1.61.К пластинам плоского воздушного конденсатора приложена разность потенциалов U1 = 500 В. Площадь пластин
S = 200 см2, расстояние между ними d = 1,5 мм. После отключения конденсатора от источника напряжения пространство между пластинами заполнили парафином (e = 2). Определите разность потенциалов U2 между пластинами после внесения диэлектрика. Определите также электроемкости конденсатора C1 и С2 до и после внесения диэлектрика. [U2 = 250 В, С1 = 118 пФ,
С2 = 236 пФ].
1.62.К пластинам плоского воздушного конденсатора приложена разность потенциалов U1 = 500 В. Площадь пластин
S = 200 см2, расстояние между ними d = 1,5 мм. При включенном источнике питания в пространство между пластинами конденсатора внесли парафин (e = 2). Определите разность потенциалов U2 между пластинами после внесения диэлектрика. Определите также электроемкости конденсатора C1 и С2 до и после внесения диэлектрика. [U2 = 500 В, С1 = 118 пФ, С2 = 236 пФ].
1.63.Плоский воздушный конденсатор электроемкостью
С = 10 пФ заряжен до разности потенциалов U1= 500 В. После отключения конденсатора от источника тока расстояние между пластинами конденсатора было увеличено в 3 раза. Определите: 1) разность потенциалов на обкладках конденсатора после их раздвижения; 2) работу внешних сил по раздвижению пластин. [1) 1,5 кВ; 2) 2,5 мкДж].
1.64.К пластинам плоского воздушного конденсатора приложено напряжение U1= 500 В. Площадь пластин S = 200 см2, расстояние между ними dl1 = 1,5 мм. Пластины раздвинули до расстояния d2 = 15 мм. Найдите энергии W1 и W2 конденсатора до и после раздвижения пластин, если источник тока перед раздвижением отключался. [W1 = 14,8 мкДж, W2 = 148 мкДж].
1.65.К пластинам плоского воздушного конденсатора приложено напряжение U1= 500 В. Площадь пластин S = 200 см2, расстояние между ними d1 = 1,5 мм. Пластины раздвинули до расстояния d2 = 15 мм. Найдите энергии W1 и W2 конденсатора до и после раздвижения пластин, если источник тока перед раздвижением не отключался. [W1 = 14,8 мкДж, W2 = 1,48 мкДж].
1.66.Расстояние между пластинами заряженного плоского конденсатора уменьшили в 2 раза. Во сколько раз изменилась энергия и плотность энергии поля, если конденсатор остался присоединеннымк источнику постоянного напряжения? [увеличилась в 2 раза, увеличилась в 4 раза].
1.67.Электроемкость батареи, образованной двумя последовательно соединенными конденсаторами, равна 100 пФ, а заряд батареи 20 нКл. Определите электроемкость второго конденсатора, а также разности потенциалов на обкладках каждого конденсатора, если электроемкость первого конденсатора200 пФ.
[С2 = 200 пФ, Dj1 = 100 В, Dj2 = 100 В].
1.68.К батарее с напряжением 300 В подключены два плоских конденсатора с электроемкостями 2 пФ и 3 пФ. Определите заряд и напряжение на пластинах конденсаторов при последовательном их соединении. [0,36 нКл; 0,36 нКл;180 В;120 В].
1.69.К батарее с напряжением 300 В подключены два плоских конденсатора с электроемкостями 2 пФ и 3 пФ. Определите заряд и напряжение на пластинах конденсаторов при параллельном их соединении. [0,6 нКл; 0,9 нКл; 300 В; 300 В].
1.70.Конденсаторы с электроемкостями 2мкФ, 5 мкФ и
10 мкФ соединены последовательно и находятся под напряжением 800 В. Определите напряжение и заряд на каждом из конденсаторов. [1 мКл; 1 мКл; 1 мКл; 500 В; 200 В; 100 В].
 2. Постоянный электрический ток
2. Постоянный электрический ток
Основные формулы и законы
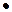 Сила тока
Сила тока
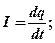
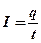 (если
(если 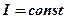 ).
).
 Плотность тока
Плотность тока
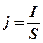 ,
, 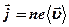 ,
,
где 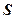 – площадь поперечного сечения проводника,
– площадь поперечного сечения проводника, 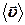 – средняя скорость упорядоченного движения зарядов в проводнике,
– средняя скорость упорядоченного движения зарядов в проводнике, 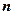 – концентрация зарядов,
– концентрация зарядов, 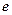 – элементарный заряд.
– элементарный заряд.
 Зависимость сопротивления от параметров проводника
Зависимость сопротивления от параметров проводника
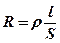 ,
,
где 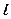 – длина проводника,
– длина проводника, 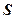 – площадь поперечного сечения проводника,
– площадь поперечного сечения проводника, 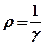 – удельное сопротивление,
– удельное сопротивление, 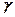 – удельная проводимость.
– удельная проводимость.
 Зависимость удельного сопротивления от температуры для металлических проводников
Зависимость удельного сопротивления от температуры для металлических проводников
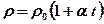 ,
,
где 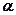 – температурный коэффициент сопротивления,
– температурный коэффициент сопротивления, 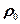 – удельное сопротивление при
– удельное сопротивление при 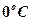 ,
, 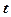 – температура проводника.
– температура проводника.
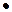 Сопротивление системы проводников: при последовательном (а) и параллельном (б) соединениях
Сопротивление системы проводников: при последовательном (а) и параллельном (б) соединениях
а) 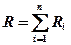 , б)
, б) 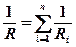 ,
,
где 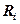 – сопротивление
– сопротивление 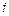 -го проводника,
-го проводника, 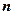 – число проводников.
– число проводников.
 Сопротивления, необходимые для расширения пределов измерения приборами силы тока (
Сопротивления, необходимые для расширения пределов измерения приборами силы тока ( 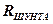 ) и напряжения (
) и напряжения ( 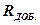 ) в
) в 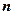 раз
раз
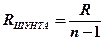 ,
, 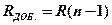 .
.
 Законы Ома:
Законы Ома:
для однородного участка цепи
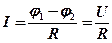 ,
,
для неоднородного участка цепи
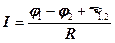 ,
,
для замкнутой цепи
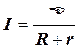 ,
,
где 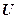 – напряжение на однородном участке цепи,
– напряжение на однородном участке цепи, 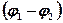 – разность потенциалов на концах участка цепи,
– разность потенциалов на концах участка цепи, 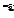 – ЭДС источника,
– ЭДС источника, 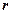 – внутреннее сопротивление источника тока, в дифференциальной форме
– внутреннее сопротивление источника тока, в дифференциальной форме
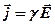 ,
,
где 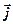 – плотность тока,
– плотность тока, 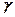 – удельная проводимость,
– удельная проводимость, 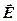 –напряжённость поля.
–напряжённость поля.
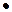 Сила тока короткого замыкания
Сила тока короткого замыкания
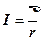 .
.
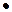 Работа тока за время
Работа тока за время 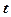
.
· Закон Джоуля-Ленца (количество теплоты, выделяемой при прохождении тока через проводник)
.
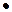 Мощность тока, выделяемая в нагрузке (полезная),
Мощность тока, выделяемая в нагрузке (полезная),
.
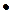 Полная мощность, выделяемая в цепи,
Полная мощность, выделяемая в цепи,
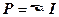 .
.
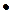 Мощность, теряемая в источнике,
Мощность, теряемая в источнике,
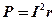 .
.
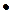 Коэффициент полезного действия источника тока
Коэффициент полезного действия источника тока
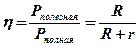 .
.
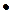 Правила Кирхгофа
Правила Кирхгофа
1) 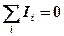 – для узлов;
– для узлов;
2) 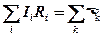 – для контуров,
– для контуров,
где 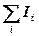 – алгебраическая сумма сил токов, сходящихся в узле,
– алгебраическая сумма сил токов, сходящихся в узле, 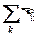 – алгебраическая сумма ЭДС в контуре.
– алгебраическая сумма ЭДС в контуре.
Задания
2.1.В сеть включены четыре последовательно соединённых резистора одинакового сопротивления. Как изменится сопротивление цепи, если эти резисторы соединить параллельно? [уменьшится в 16 раз].
2.2.В сеть с напряжением 120 В включены две лампы сопротивлением 200 Ом каждая. Какой ток пойдёт через каждую лампу при параллельном и последовательном их соединениях? [0,6 А; 0,3 А].
2.3.Общее сопротивление двух последовательно соединённых проводников 5 Ом, а параллельно соединённых 1,2 Ом. Определите сопротивление каждого проводника. [3 Ом и 2 Ом].
2.4.Сопротивление одного из последовательно включённых проводников в n раз больше сопротивления другого. Во сколько раз изменится сила тока в цепи (напряжение постоянно), если проводники включить параллельно? [увеличится в (n+1)2/n раз].
2.5. На концах медного провода длиной 5 м поддерживается напряжение 1 В. Определите плотность тока в проводе (удельное сопротивление меди 1,7.10-8 Ом . м). [1,18.107А/м2].
2.6.Во сколько раз изменится сопротивление проводника (без изоляции), если его свернуть пополам и скрутить? [уменьшится в 4 раза].
2.7. Гальванический элемент даёт на внешнее сопротивление 0,5 Ом силу тока 0,2 А. Если внешнее сопротивление заменить на 0,8 Ом, то ток в цепи 0,15 А. Определите силу тока короткого замыкания. [0,45A] .
2.8. Резистор сопротивлением 5 Ом, вольтметр и источник тока соединены параллельно. Вольтметр показывает напряжение 10 В. Если заменить резистор другим с сопротивлением 12 Ом, то вольтметр покажет напряжение 12 В. Определите ЭДС и внутреннее сопротивление источника тока. Током через вольтметр пренебречь. [14 В; 2 Ом].
2.9.Найдите внутреннее сопротивление и ЭДС источника тока, если при силе тока 30 А мощность во внешней цепи равна 180 Вт, а при силе тока 10 А эта мощность равна 100 Вт. [0,2 Ом; 12 В].
2.10.  Определите силу тока в цепи, состоящей из двух элементов с ЭДС, равными 1,6 В и 1,2 В и внутренними сопротивлениями 0,6 Ом и 0,4 Ом соответственно, соединённых одноимёнными полюсами. [0,4 A] .
Определите силу тока в цепи, состоящей из двух элементов с ЭДС, равными 1,6 В и 1,2 В и внутренними сопротивлениями 0,6 Ом и 0,4 Ом соответственно, соединённых одноимёнными полюсами. [0,4 A] .
2.11.Электрическую лампу сопротивлением 240 Ом, рассчитанную на напряжение 120 В, надо питать от сети напряжением 220 В. Какой длины нихромовый проводник с площадью поперечного сечения 0,55 мм2 надо включить последовательно с лампой? (удельное сопротивление нихрома 1,1.10-6 Ом.м). [100 м].
2.12.Цепь состоит из трёх последовательно соединённых проводников, подключенных к источнику напряжения 24 В. Сопротивление первого проводника 4 Ом, второго 6 Ом, а напряжение на концах третьего проводника 4 В. Найдите силу тока в цепи, сопротивление третьего проводника и напряжения на концах первого и второго проводников. [2 А; 2 Ом; 8 В; 12 В].
2.13. К источнику тока с ЭДС 12 В присоединена нагрузка. Напряжение на клеммах источника 8 В. Определите КПД источника тока. [68%] .
2.14.Внешняя цепь источника тока потребляет мощность 0,75 Вт. Определите силу тока в цепи, если ЭДС источника 2 В и внутреннее сопротивление 1 Ом. [0,5 А и 1,5 А] .
2.15.Источник тока с ЭДС 12 В и внутренним сопротивлением 1 Ом подключён к нагрузке сопротивлением 9 Ом. Найдите: 1) силу тока в цепи, 2) мощность, выделяемую во внешней части цепи, 3) мощность, теряемую в источнике тока, 4) полную мощность источника тока, 5) КПД источника тока. [1)1,2 A; 2)12,96 Вт; 3)1,44 Вт; 4)14,4 Вт; 5)90%].
2.16.Обмотка электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через 10 мин, если другая, то через 20 мин. Через сколько минут закипит вода, если обе секции включить последовательно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми. [30 мин].
2.17.Обмотка электрического кипятильника имеет две секции. Если включена одна секция, вода закипает через 10 мин, если другая, то через 20 мин. Через сколько минут закипит вода, если обе секции включить параллельно? Напряжение на зажимах кипятильника и КПД установки считать во всех случаях одинаковыми. [6,67 мин] .
2.18.Амперметр сопротивлением 0,18 Ом предназначен для измерения силы тока до 10 А. Какое сопротивление надо взять и как его включить, чтобы этим амперметром можно было измерять силу тока до 100 А? [0,02 Ом, параллельно].
2.19.Вольтметр сопротивлением 2000 Ом предназначен для измерения напряжения до 30 В. Какое сопротивление надо взять и как его включить, чтобы этим вольтметром можно было измерять напряжение до 75 В? [3000 Ом, последовательно].
2.20. Ток в проводнике сопротивлением 100 Ом равномерно нарастает от 0 до 10 А в течение 30 с. Чему равно количество теплоты, выделившееся за это время в проводнике? [100 кДж].
2.21. Ток в проводнике сопротивлением 12 Ом равномерно убывает от 5 А до 0 в течение 10 с. Какое количество теплоты выделяется в проводнике за это время? [1 кДж].
2.22. По проводнику сопротивлением 3 Ом течёт равномерно возрастающий ток. Количество теплоты, выделившееся в проводнике за 8 с, равно 200 Дж. Определите заряд, протекший за это время по проводнику. В начальный момент времени ток был равен нулю. [20 Кл].
 2.23. Ток в проводнике сопротивлением 15 Ом равномерно возрастает от 0 до некоторого максимума в течение 5 с. За это время в проводнике выделилось количество теплоты 10 кДж. Найдите среднее значение силы тока в проводнике за этот промежуток времени. [10 А] .
2.23. Ток в проводнике сопротивлением 15 Ом равномерно возрастает от 0 до некоторого максимума в течение 5 с. За это время в проводнике выделилось количество теплоты 10 кДж. Найдите среднее значение силы тока в проводнике за этот промежуток времени. [10 А] .
2.24. Ток в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение 10 с. За это время в проводнике выделилось количество теплоты 1 кДж. Определите скорость нарастания тока в проводнике, если сопротивление его 3 Ом. [1А/с].
2.25. На рис. 2.1  =
=  =
=  , R1 = 48 Ом, R2 = 24 Ом, падение напряжения U2 на сопротивлении R2 равно 12 В. Пренебрегая внутренним сопротивлением элементов, определите силу тока во всех участках цепи и сопротивление R3. [I1=0,25 A, I2=0,5 A, I3=0,75 A, R3=16 Ом].
, R1 = 48 Ом, R2 = 24 Ом, падение напряжения U2 на сопротивлении R2 равно 12 В. Пренебрегая внутренним сопротивлением элементов, определите силу тока во всех участках цепи и сопротивление R3. [I1=0,25 A, I2=0,5 A, I3=0,75 A, R3=16 Ом].
|
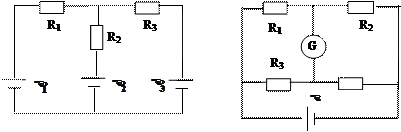
Рис. 2.1. Рис.2.2.
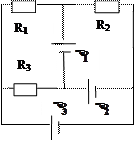 |
Рис. 2.3
2.26. На рис. 2.2  =2В, R1= 60 Ом, R2= 40 Ом, R3=R4= 20 Ом, RG= 100 Ом. Определите силу тока IG через гальванометр. [1,49 мА].
=2В, R1= 60 Ом, R2= 40 Ом, R3=R4= 20 Ом, RG= 100 Ом. Определите силу тока IG через гальванометр. [1,49 мА].
2.27. Найдите силу тока в отдельных ветвях мостика Уитстона (рис. 2.2) при условии, что сила тока, идущего через гальванометр, равна нулю. ЭДС источника 2В, R1= 30 Ом, R2= 45 Ом, R3= 200 Ом. Внутренним сопротивлением источника пренебречь. [I1=I2=26,7 мА, I3=I4= 4 мА].
2.28. На рис. 2.3  =10 В,
=10 В,  = 20 В,
= 20 В, 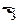 = 40 В, а сопротивления R1=R2=R3= 10 Ом. Определите силу токов через сопротивления (I) и через источники (
= 40 В, а сопротивления R1=R2=R3= 10 Ом. Определите силу токов через сопротивления (I) и через источники ( 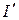 ). Внутренним сопротивлением источников пренебречь. [I1=1A, I2=3A, I3=2A,
). Внутренним сопротивлением источников пренебречь. [I1=1A, I2=3A, I3=2A, 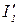 =2A,
=2A, 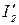 =0,
=0, 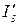 =3A].
=3A].
2.29. На рис. 2.4 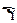 = 2,1 В,
= 2,1 В, 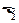 = 1,9 В, R1=45 Ом, R2= 10 Ом, R3= 10 Ом. Найдите силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь. [I1=0,04 A, I2=0,01 A, I3=0].
= 1,9 В, R1=45 Ом, R2= 10 Ом, R3= 10 Ом. Найдите силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь. [I1=0,04 A, I2=0,01 A, I3=0].

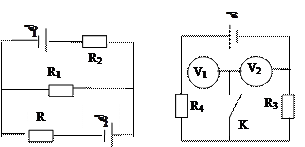
Рис. 2.4 Рис. 2.5
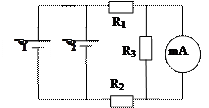
Рис. 2.6
2.30. На рис. 2.5 сопротивления вольтметров равны R1=3000 Ом и R2=2000 Ом; R3=3000 Ом, R4=2000 Ом; 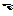 =200 В. Найдите показания вольтметров в случаях: а) ключ К разомкнут, б) ключ К замкнут. Внутренним сопротивлением источника пренебречь. [а) U1=120 В, U2=80 В; б) U1=U2=100 В].
=200 В. Найдите показания вольтметров в случаях: а) ключ К разомкнут, б) ключ К замкнут. Внутренним сопротивлением источника пренебречь. [а) U1=120 В, U2=80 В; б) U1=U2=100 В].
2.31. На рис. 2.6 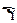 =
= 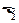 =1,5 В, внутренние сопротивления источников r1=r2=0,5 Ом, R1=R2= 2 Ом, R3= 1 Ом. Сопротивление миллиамперметра 3 Ом. Найдите показание миллиамперметра. [75 мА].
=1,5 В, внутренние сопротивления источников r1=r2=0,5 Ом, R1=R2= 2 Ом, R3= 1 Ом. Сопротивление миллиамперметра 3 Ом. Найдите показание миллиамперметра. [75 мА].
2.32. На рис. 2.7 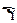 =
= 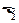 = 110 В, R1=R2= 200 Ом, сопротивление вольтметра 1000 В. Найдите показание вольтметра. Внутренним сопротивлением источников пренебречь. [100 В].
= 110 В, R1=R2= 200 Ом, сопротивление вольтметра 1000 В. Найдите показание вольтметра. Внутренним сопротивлением источников пренебречь. [100 В].

Рис. 2.7 Рис. 2.8
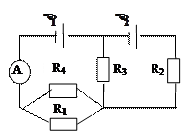
Рис. 2.9
2.33. На рис. 2.8 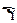 =
= 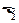 = 2В, внутренние сопротивления источников равны 0,5 Ом, R1= 0,5 Ом, R2= 1,5 Ом. Найдите силу тока во всех участках цепи. [2,22 А; 0,44 А; 1,78 А].
= 2В, внутренние сопротивления источников равны 0,5 Ом, R1= 0,5 Ом, R2= 1,5 Ом. Найдите силу тока во всех участках цепи. [2,22 А; 0,44 А; 1,78 А].
2.34. На рис. 2.9 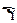 =
= 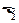 = 100 В, R1= 20 Ом, R2= 10 Ом, R3= 40 Ом, R4= 30 Ом. Найдите показание амперметра. Внутренним сопротивлением источников и амперметра пренебречь. [1 А].
= 100 В, R1= 20 Ом, R2= 10 Ом, R3= 40 Ом, R4= 30 Ом. Найдите показание амперметра. Внутренним сопротивлением источников и амперметра пренебречь. [1 А].
2.35. Какую силу тока показывает амперметр на рис. 2.10, сопротивление которого RA=500 Ом, если 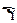 = 1 В,
= 1 В,  = 2 В, R3=1500 Ом и падение напряжения на сопротивлении R2 равно 1 В. Внутренним сопротивлением источников пренебречь.[1 мА].
= 2 В, R3=1500 Ом и падение напряжения на сопротивлении R2 равно 1 В. Внутренним сопротивлением источников пренебречь.[1 мА].
2.36. На рис. 2.11  =1,5 В,
=1,5 В,  =1,6 В, R1=1 кОм, R2=2 кОм. Определите показания вольтметра, если его сопротивление
=1,6 В, R1=1 кОм, R2=2 кОм. Определите показания вольтметра, если его сопротивление
RV=2 кОм. Сопротивлением источников пренебречь. [0,35 В].
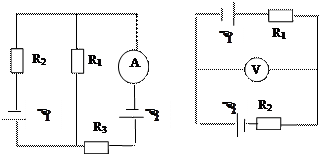
Рис. 2.10 Рис. 2.11
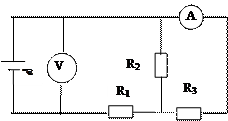
Рис. 2.12
2.37. На рис. 2.12 сопротивления R1= 5Ом, R2= 6 Ом,
R3= 3 Ом. Найдите показание амперметра, если вольтметр показывает 2,1 В. Сопротивлением источника и амперметра пренебречь. [0,2 А].
2.38. Определите ЭДС источника в схеме на рис. 2.13, если сила тока, текущего через него, равна 0,9 А, внутреннее сопротивление источника 0,4 Ом. R1=30 Ом, R2=24 Ом, R3 =50 Ом,
R4 =40 Ом, R5 =60 Ом.
2.39. Найдите показания амперметра в схеме на рис. 2.14, если ЭДС равна 19,8 В, внутреннее сопротивление 0,4 Ом, R1=30 Ом, R2=24 Ом, R3=50 Ом, R4=40 Ом, R5=60 Ом.
 |

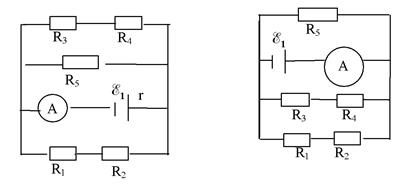
Рис. 2.13 Рис. 2.14
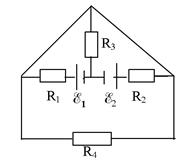
Рис. 2.15
2.40. Найдите величины всех сопротивлений в схеме на рис. 2.15, если через сопротивление R1 течёт ток 0,4 мкА, через сопротивление R2 ток 0,7 мкА, через сопротивление R3 – 1,1 мкА, через сопротивление R4 ток не течёт. Внутренним сопротивлением элементов пренебречь. 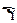 =1,5 В;
=1,5 В; 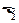 =1,8 В.
=1,8 В.
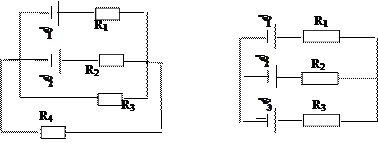
Рис. 2.16 Рис. 2.17

Рис. 2.18
2.41. Определите 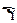 и
и 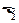 в схеме на рис. 2.16, если R1=R4=2 Ом, R2=R3= 4 Ом. Ток, текущий через сопротивление R3, равен 1А, а через сопротивление R2 ток не течёт. Внутренние сопротивления элементов r1=r2=0,5 Ом.
в схеме на рис. 2.16, если R1=R4=2 Ом, R2=R3= 4 Ом. Ток, текущий через сопротивление R3, равен 1А, а через сопротивление R2 ток не течёт. Внутренние сопротивления элементов r1=r2=0,5 Ом.
