Циліндричного конденсаторІВ
8.1 Мета роботи
Дослідити розподіл потенціалу в електричних полях: одновимірної послідовності N-точкових зарядів; циліндричного конденсатора; плоского конденсатора та вплив на розподіл поля обмеженості розмірів його пластин.
8.2 Вказівки до організації самостійної роботи
Силовою характеристикою електричного поля в кожній точці є вектор напруженості  , а енергетичною характеристикою – потенціал
, а енергетичною характеристикою – потенціал 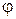 . Електричне поле будь-якої системи зарядів можна зобразити за допомогою ліній напруженості або еквіпотенціальних ліній. Лінії (або поверхні), вздовж яких потенціал не змінюється:
. Електричне поле будь-якої системи зарядів можна зобразити за допомогою ліній напруженості або еквіпотенціальних ліній. Лінії (або поверхні), вздовж яких потенціал не змінюється:  , мають назву еквіпотенціальних ліній (або поверхонь). Лінії напруженості завжди ортогональні еквіпотенціальним лініям (поверхням), причому в кожній точці електричного поля [2, 5]
, мають назву еквіпотенціальних ліній (або поверхонь). Лінії напруженості завжди ортогональні еквіпотенціальним лініям (поверхням), причому в кожній точці електричного поля [2, 5]
 , (8.1)
, (8.1)
де  ,
,  ,
,  − одиничні вектори спрямовані вздовж осей x, y, z.
− одиничні вектори спрямовані вздовж осей x, y, z.
Знак “−” у формулі (8.1) означає, що градієнт потенціалу(векторна величина) спрямований протилежно вектору  . Сам градієнт спрямований в бік найшвидшого зростання потенціалу.
. Сам градієнт спрямований в бік найшвидшого зростання потенціалу.
Потенціал точкового заряду визначається за формулою
 , (8.2)
, (8.2)
де 
 Ф/м − електрична стала; q − точковий заряд, r − відстань від заряду до точки спостереження.
Ф/м − електрична стала; q − точковий заряд, r − відстань від заряду до точки спостереження.
Потенціал системи точкових зарядів в даній точці А обчислюється за формулою
 , (8.3)
, (8.3)
де  – точковий заряд однієї послідовності зарядів;
– точковий заряд однієї послідовності зарядів;
 – точковий заряд другої послідовності зарядів;
– точковий заряд другої послідовності зарядів;
x, y – координати радіус-вектора, що характеризує положення точки, в якій визначається потенціал;
 ,
, 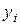 ,
,  j,
j,  – координати радіус-вектора, який характеризує відповідно до положення і-го та j-го заряду (рис.8.1).
– координати радіус-вектора, який характеризує відповідно до положення і-го та j-го заряду (рис.8.1).
Враховуючи широкі можливості комп’ютера, ми відразу розглядаємо поле дискретної послідовності зарядів. Можна було б розглядати заряд, розподілений безперервно вздовж ліній. Але такий підхід є складнішим, бо в цьому випадку потенціал необхідно визначати через інтеграли, а потім знову ж таки наближено їх обчислювати, розбиваючи лінії, вздовж яких розподілені заряди, на окремі відрізки, тобто заміняти інтеграл наближеною сумою вигляду (8.3).


a) б)
Рисунок 8.1
Потенціал дискретної послідовності числа n зарядів величиною q відрізнятиметься від рівномірного розподілу з еквівалентною лінійною густиною τ лише безпосередньо біля зарядів (в цьому можна впевнитися під час виконання даної роботи, будуючи еквіпотенціальні лінії поля). У випадку, коли заряди знаходяться на прямій (рис.8.1а ), лінійна густина заряду
 ,
,
де  і
і  – відповідні x-координати першого та n-го зарядів. Коли заряди розташовані по колу (рис.8.1б), маємо
– відповідні x-координати першого та n-го зарядів. Коли заряди розташовані по колу (рис.8.1б), маємо
 ,
,
де R – радіус кола.
Для нескінченно довгих пластин і циліндрів картина еквіпотенціальних ліній в площині, перпендикулярній до них(в площині рисунка) буде такою самою, як і для лінійного розподілу зарядів з лінійною густиною  .
.
8.3 Опис комп’ютерної програми
Зовнішній вигляд інтерфейсу програми зображено на рис. 8.2. Програма дозволяє створювати такі розподіли зарядів: один точковий заряд, диполь, заряджена смуга, дві паралельні смуги, два коаксіальні циліндри і таким чином моделювати плоский та циліндричний конденсатори. Програма дає можливість знайти точки однакового потенціалу для вказаних розподілів зарядів.
"Вимірювання" потенціалу в будь-якій точці з координатами (х, у) здійснюється за допомогою "зонда", роль якого відіграє курсор "мишки". Натискаючи ліву клавішу "мишки" в деякій точці отримуємо на екрані висвітлені координати точки та значення потенціалу. За отриманими даними користувач має можливість побудувати еквіпотенціальні лінії поля даної системи зарядів, а також обчислити напруженість поля.

Рисунок 8.2
Кількість зарядів, відстань між ними можна змінювати в широких межах, досягаючи такої густини зарядів, коли немає великої різниці між дискретним і безперервним розподілом. Користувач може прослідкувати, як впливає дискретність розподілу зарядів на форму еквіпотенціальних ліній.
8.4 Інструкція користувачу
1. Створіть один точковий заряд  (значення
(значення  візьміть з табл. 8.1). Відшукайте точки однакового потенціалу для точок, розташованих на відстані від заряду
візьміть з табл. 8.1). Відшукайте точки однакового потенціалу для точок, розташованих на відстані від заряду  ;
;  ;
;  ;
;  . З’єднайте точки з однаковим потенціалом (
. З’єднайте точки з однаковим потенціалом (  ), отримайте еквіпотенціальні лінії.
), отримайте еквіпотенціальні лінії.
2. Обчисліть тричі наближено значення напруженості за формулою
 . (8.4)
. (8.4)
Значення  і
і  візьміть для двох сусідніх еквіпотенціальних ліній. Обчисліть напруженість електричного поля як градієнт потенціалу, зробивши вимірювання
візьміть для двох сусідніх еквіпотенціальних ліній. Обчисліть напруженість електричного поля як градієнт потенціалу, зробивши вимірювання  ,
,  в двох будь-яких близьких точках, які знаходяться на сусідніх еквіпотенціальних лініях (рис.8.3), за формулою, аналогічною (8.1)
в двох будь-яких близьких точках, які знаходяться на сусідніх еквіпотенціальних лініях (рис.8.3), за формулою, аналогічною (8.1)

 . (8.5)
. (8.5)
3. Порівняйте результати, отримані за формулами (8.4) і (8.5).
4. Створіть системи точкових зарядів, розташованих паралельно одна одній, значення q, n, і  візьміть з табл. 8.1, заряд однієї системи зарядів +q, другої – q (порядок величини q~10-12...10-14 Кл).
візьміть з табл. 8.1, заряд однієї системи зарядів +q, другої – q (порядок величини q~10-12...10-14 Кл).
5. Знайдіть точки однакового потенціалу, починаючи з точки, що знаходиться на перетині осей симетрії системи (рис.8.1, а). Зробіть аналогічні заміри, щоб побудувати не менше трьох еквіпотенціальних ліній, розміщених між лінією розташування зарядів та лінією симетрії, яка проходить посередині між системами. Зробіть заміри для точок не тільки всередині системи зарядів, а й для зовнішніх точок, де вже буде добре видно, що еквіпотенціальні лінії стають непаралельними одна одній.
6. Обчисліть напруженість поля поблизу точки С (рис.8.1, а) – в центрі системи. Якщо еквіпотенціальні лінії паралельні, то поле однорідне і величину напруженості поля в конденсаторі можна обчислити за формулою.
 . (8.6)
. (8.6)
Порівняйте отриманий результат з результатом, обчисленим за формулою, справедливою для випадку двох нескінченних паралельних площин
 . (8.7)
. (8.7)
7. Виконайте завдання пунктів 4…6 для “пластин”, ширина яких перевищує вибрану в пункті 3 в декілька m разів (дані в табл. 8.1). Як розміри пластин впливають на характер поля?
8. Створіть дві системи зарядів, розташованих на концентричних колах з радіусами 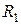 і
і  (дані пункту 8). Центр кіл оберіть так, щоб вони не вийшли за межі осей x, y. Заряд
(дані пункту 8). Центр кіл оберіть так, щоб вони не вийшли за межі осей x, y. Заряд  і
і  підберіть так, щоб заряд однієї “пластини”
підберіть так, щоб заряд однієї “пластини”  конденсатора дорівнював
конденсатора дорівнював  – заряду другої “пластини”. Побудуйте не менше трьох еквіпотенціальних ліній.
– заряду другої “пластини”. Побудуйте не менше трьох еквіпотенціальних ліній.
Порівнюючи форму еквіпотенціальних ліній для плоских і циліндричних пластин зробіть належний висновок щодо відповідності між формою ліній та пластин.
Таблиця 8.1 – Вихідні дані
| Номер |  ·10-5, Кл ·10-5, Кл |  ·10-5, Кл ·10-5, Кл |  , мм , мм | n | m | 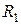 , мм , мм |  , мм , мм |
8.5 Зміст звіту
Звіт має містити: мету роботи, рисунки побудованих еквіпотенціальних ліній, результати розрахунків (пункти 2, 6) та висновки до пунктів 7, 8.
8.6 Контрольні запитання і завдання
1. Запишіть формулу потенціалу точкового заряду.
2. За якою формулою визначається потенціал системи точкових зарядів?
3. Запишіть формулу зв’язку напруженості поля з потенціалом.
4. Опишіть властивості градієнта.
5. Що таке еквіпотенціальні лінії (поверхні)? Під яким кутом перетинаються лінії напруженості з еквіпотенціальними лініями?
6. Вивести формули для потенціалу поля в циліндричному та плоскому конденсаторі.
7. Що таке лінійна густина заряду?
