Определение размеров бликующих зон поверхности БЭК, которые необходимо перекрыть рассеивающими конфигурациями

В безэховой камере передающая антенна, как и приемная, на­ходятся на конечном расстоянии друг от друга и от рабочей по­верхности. Как правило, эти расстояния, так же как и размеры камеры, много больше длины волны. В большинстве случаев ка­мера представляет собой прямоугольный объем, ограниченный шестью плоскостями, покрытыми поглощающим материалом. По­этому, прежде всего, необходимо рассмотреть отражения от пло­скости, покрытой радиопоглощающим материалом, и методы уменьшения этих отражений.

Задача отражения сферической волны источника, находящего­ся на конечном расстоянии от плоской границы сред, рассмотрена в ряде работ. Воспользуемся решением, приведенным в моногра­фии Бреховских [70] для сферической волны, падающей на пло­скую границу раздела, характеризуемую коэффициентом отраже­ния R(q).В работе проведена обычная процедура разложения сферической волны на совокупность плоских, найдены составляю­щие отраженной волны с помощью заданной зависимости R(q)и проведено вычисление полученных интегралов по методу перева­ла в предположении больших расстояний до источника кr_р>>1.В результате получено выражение коэффициента отражения сфе­рической волны R_cисточника, находящегося на расстоянии г_р,

R_c = 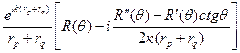. (3.24)

где R(q)— френелевский коэффициент отражения плоской волны, падающей под углом q вдоль пути стационарной фазы для отра­женного поля r_p + r_q; R'(q) и R"(q) — первая и вторая производ­ные угловой характеристики френелевского коэффициента отра­жения при угле q.

Если вблизи угла падения q френелевский коэффициент отражения изменяется достаточно медленно:

R(q) >> 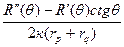, (3.25)

то сферическая волна отражается от плоской границы раздела с тем же коэффициентом отражения, что и плоская, падающая на границу под углом q,

R_c » 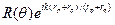. (3.26)

Этим свойством сферической волны широко пользуются в прак­тических расчетах отражений от плоскостей, ограничивающих объем безэховой камеры, так как у большинства РПМ для рабо­чей области углов q неравенство (3.25) соблюдается.

Если допустимый уровень отражения, определяемый заданной точностью измерений, меньше того, который определяется свойст­вом РПМ: R_доп << R(q),то для снижения уровня отраженных сиг­налов необходимо исключить отражения от интенсивно бликующих частей плоскости, прилегающих к точке стационарной фазы.

Обычно это достигается установкой на плоскости рассеиваю­щих поглощающих конфигураций, которые отражают поле в пе­риферийные части объема камеры, где оно ослабляется из-за мно­гократных отражений от поверхности, покрытой РПМ.

Не останавливаясь пока на расчете этих конфигураций, опре­делим размеры части отражающей плоскости, которую необходи­мо исключить. При этом критерием достаточности пространства является условие, чтобы оставшаяся часть плоской поверхности, покрытая РПМ, не создавала отражений, превышающих допусти­мые.

Поле, отраженное от плоскости с коэффициентом отражения R(q), из которой вокруг точки стационарной фазы вынут прямо­угольник с размерами а и b (рис. 3.5), может быть записано в виде

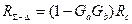, (3.27)

где G_aи G_b — френелевский коэффициент ослабления поля при отражении от прямоугольника размерами а и b с центром в бликующей точке,

G(u) = e^ip/4[F(u) - F(-u)]/ 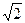, (3.28)

F(u) 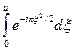- интеграл Френеля от аргумента и:

u 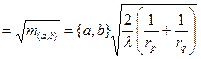(3.29)

Аргумент интеграла Френеля и равен корню из количества зон Френеля, уложившихся в соответствующем размере.

Используя асимптотическое разложение интеграла Френеля (см., например, [80])

F(u) = 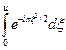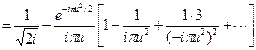(3.30)

и ограничиваясь для больших значений аргумента первыми дву­мя членами разложения, получим

F(u) 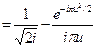(3.31)

По-видимому, размеры прямоугольника исключаемой части отражающей плоскости целесообразно выбрать такими, чтобы из­бежать равного количества зон по обоим направлениям m_а = m_ь = m. Тогда с учетом (3.28)

G_aG_b = G² 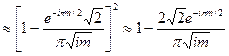. (3.32)

Ослабление поля, отраженного от плоскости, за счет изъятия т первых зон Френеля

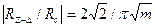. (3.33)

Полагая

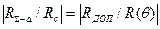, (3.34)

получим неравенство, позволяющее определить количество зон Френеля, которые необходимо исключить из отражающей пло­скости,

m ³ (8/p²)×[R²(q)/R²_доп]. (3.35)

Пусть, например, R²(q) =3% (или 1%), а R²_доп=0,01%, тогда в соответствии с (3.35) m ³ 243 (или 81). Для поглощающих мате­риалов среднего качества, имеющих коэффициент отражения (1¸3)%, приходится исключать значительное количество зон Френеля.

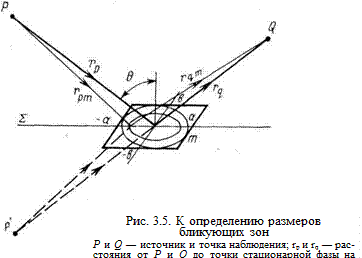
Определим линейные размеры зон на отражающей пло­скости, которые необходимо перекрыть конфигурациями.

Как видно из (3.26), поверхности равных фаз поля точечного источника, отраженного от плоскости, представляют собой систе­му конфокальных эллипсов вида

r_pm + r_qm = 2F + ml/4, 2F = r_p + r_q, (3.36), (3,37)

с фокусами в точках р'и Q (рис. 3.5); F=const — фокусное рас­стояние эллипса. Большая ось эллипса a_mдля m-зоны Френеля может быть найдена из соотношения F + a_m=r_pm+r_qm:

a_m = F + ml/4. (3.38)

Малая ось эллипса 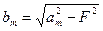, т.е.

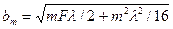. (3.39)

Координата центра эллипса относительно точки пересечения с плоскостью отражения

x₀ = r_q - (r_q + r_p)/2 = (r_q - r_p)/2 . (3.40)

В частном случае r_p = r_q,x₀ = 0,

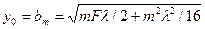. (3.41)

Размер большой полуоси эллипса в плоскости отражения удоб­но определить, используя соотношение

a = b/cosq, (3.42)

где q — угол падения луча стационарной фазы на отражающую

плоскость S.

В случае ml/4<<F для r_p= r_q= r

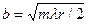. (3.41¢)

Выражение (3.41') совпадает с приближенными выражениями, обычно встречающимися в литературе [80].

В общем случае r_p¹ r_qмалая полуось эллипса m-зоны Френе­ля в плоскости отражения S может быть найдена из каноническо­го уравнения эллипса для х₀, определенного в соответствии с (3.40). Тогда

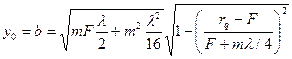
С учетом (3.37)

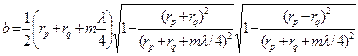. (3.43)

Выражение (3.43) является наиболее общим и позволяет опреде­лить размеры малой полуоси, а с помощью (3.42) и большой по­луоси эллипса в плоскости отражения, которые соответствуют т первым зонам Френеля на отражающей плоскости. Для ml/4<<F

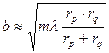, (3.43¢)

Это выражение также совпадает с приводимым в [80].

Однако, как мы видели при обсуждении выражения (3.35), в безэховых камерах оказывается необходимым исключить значи­тельное количество зон Френеля вблизи точки стационарной фазы на ограничивающих поверхностях. Поэтому неравенство ml/4<<Fсоблюдается не всегда, и при определении размеров части пло­скости, которую необходимо перекрыть конфигурацией, следует использовать более общее выражение (3.43). Так, при r_p= r_q= 50l и m=100 использование приближенной формулы (3.43') вместо (3.43) дает занижение требуемого размера на 10%.