Описание лабораторного макета. Лабораторная работа выполняется на компьютере в среде HP VEE с использованием виртуального макета, структурную схему которого приведено на рис

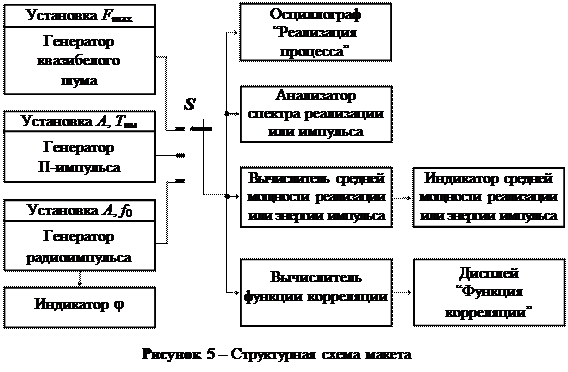
Лабораторная работа выполняется на компьютере в среде HP VEE с использованием виртуального макета, структурную схему которого приведено на рис. 5. Макет содержит следующие генераторы:

- генератор шума, который формирует реализацию квазибелого шума в интервале частот (0, F_max) длительностью 20 мс в виде 5000 отсчетов; макет дает возможность установить значения F_max 1000, 2000 и 3000 Гц;

- генератор одиночного П-импульса, которому можно установить длительность импульса 0,5, 1 и 1,5 мс и произвольную амплитуду;

- генератор радиоимпульса с П-образной огибающей длительностью 2 мс позволяет установить произвольную амплитуду импульса и частоту колебания f₀ 1000, 2000 и 3000 Гц; фаза колебания является случайной величиной, ее значение выводится на индикатор j.

Переключатель S позволяет выбрать исследуемый процесс.

Если для исследования выбран шум, то на дисплеях отображаются:

- реализация шума;

- значение измеренной средней мощности реализации;

- корреляционная функция реализации, рассчитанная по алгоритму, приведеному на рис. 2;

- спектральная плотность мощности реализации шума, полученная как преобразование Фурье от корреляционной функции реализации; программа формирует отсчеты квазибелого шума, однако из-за малого количества отсчетов (5000 отсчетов) спектр далеко не белый в полосе частот (0, F_max).

Если для исследования выбрано П-импульс или радиоимпульс, то на дисплеях отображаются:

- осциллограмма импульса;

- значение измеренной энергии импульса;

- корреляционная функция импульса, рассчитанная по формуле (7);

- квадрат амплитудного спектра импульса, полученного как преобразование Фурье от корреляционной функции импульса.

Во всех случаях для вычисления КФ используется встроенная функция Xcorrelate.

Требования к отчету

7.1 Название лабораторной работы.

7.2 Цель работы.

7.3 Результаты выполнения домашнего задания.

7.4 Структурные схемыисследований и результаты выполнения пп. 5.2...5.4 лабораторного задания (графики и числовые значения).

7.5 Выводы по каждому пункту задания, в которых предоставить анализ полученных результатов (проверка выполнения свойств корреляционных функций, совпадение экспериментальных и теоретических данных).

7.6 Дата, подпись студента, виза преподавателя с оценкой в 100-балльной системе оценивания.

ЛР 1.4 Исследование сигналов аналоговой модуляции

Цель работы

1.1 Исследование временных и спектральных характеристик сигналов аналоговых видов модуляции.

1.2 Исследование связи между характеристиками модулированных и модулирующих сигналов.

Ключевые положения

2.1 Модуляция является аналоговой, если модулирующий сигнал аналоговый. Принцип аналоговой модуляции: имеется вспомогательное гармоническое колебание – переносчик u_пер(t) = a₀ cos(2pf₀t + j ₀); при модуляции один из параметров переносчика получает приращения, пропорциональные значениям модулирующего сигнала b(t). У такого переносчика пр модуляции могут получать приращения: амплитуда, частота или начальная фаза. Название параметра, который получает приращения, определяет название модуляции: амплитудная (АМ), фазовая (ФМ) и частотная (ЧМ).

В случае аналоговых видов модуляции модулирующий сигнал – это первичный непрерывный сигнал электросвязи b(t) с такими характеристиками:

- максимальная частота спектра сигнала F_max;

- сигнал нормирован так, что максимальное по модулю значение ïb(t)ï_max = 1;

- среднее значение сигнала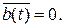

2.2 В случае АМ приращение амплитуды переносчика пропорционально мгновенным значением модулирующего сигнала, т.е. амплитуда модулированного сигнала 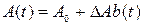, где DA – коэффициент пропорциональности, который выбирают так, чтобы амплитуда A(t) не принимала отрицательных значений. Поскольку ïb(t)ï_max = 1, то DA определяет наибольшее по модулю приращение амплитуды переносчика, а, чтобы амплитуда A(t) не принимала отрицательных значений, необходимо обеспечить DA £ a₀. Частота и начальная фаза переносчика остаются неизменными. Удобно перейти к относительному максимальному приращению амплитуды – коэффициенту амплитудной модуляции m_АМ = DA/a₀. Ясно, что 0 < m_АМ £ 1.

Аналитическое выражение сигнала АМ при произвольном модулирующем сигнале имеет вид

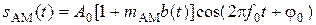. (1)

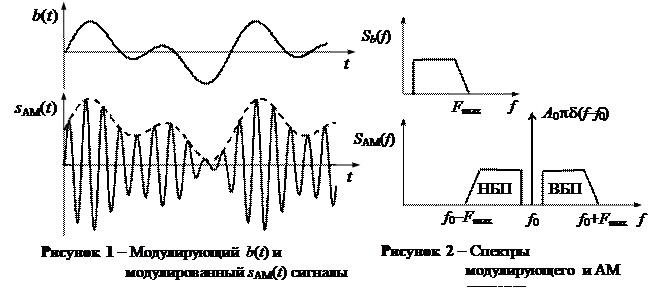
Видим, что параметрами сигнала АМ являются m_АМ, a₀, f₀ и j₀. Временную диаграмму сигнала АМ приведено на рис. 1. Обращает на себя внимание то, что огибающая модулированного сигнала повторяет форму модулирующего сигнала – амплитуда сигнала АМ A(t) является огибающей высокочастотного колебания cos(2pf₀t + j₀) (на рис. 1 огибающая изображена штриховой линией).

2.3 На рис. 2 показано произвольный амплитудный спектр модулирующего сигнала и соответствующий ему амплитудный спектр сигнала АМ, который состоит из гармонического колебания частоты переносчика, верхней боковой полосы частот (ВБП) и нижней боковой полосы частот (НБП). При этом ВБП является масштабной копией спектра модулирующего сигнала, которая сдвинута по частоте на величину f₀. НБП является зеркальным отображением ВБП относительно частоты переносчика f₀.

Из рис. 2 вытекает важный результат: ширина спектра сигнала АМ DF_АМ равняется удвоенному значению максимальной частоты спектра модулирующего сигнала, т.е. DF_АМ = 2F_max.

2.4 Расчеты показывают, что, когда модулирующими сигналами являются первичные сигналы электросвязи, то часть мощности боковых полос составляет лишь несколько процентов от мощности модулированного сигнала. Поэтому целесообразно сформировать сигнал со спектром, который состоит лишь из двух боковых полос частот (колебание частоты переносчика отсутствует), – таким сигналом является сигнал балансной модуляции.

Балансной называется такой вид модуляции, когда модулированным сигналом является произведение модулирующего сигнала и переносчика. Аналитическое выражение сигнала БМ имеет вид

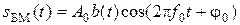. (2)

Временные диаграммы модулирующего и модулированного сигналов приведены на рис. 3. Поскольку модулирующий сигнал действует на амплитуду переносчика, то БМ считается разновидностью АМ. Из рис. 3 видно, что огибающая сигнала БМ A(t) = A₀½b(t)½ (показана пунктирной линией) не повторяет модулирующий сигнал.

Из сравнения математических выражений, описывающих сигнал АМ (1) и сигнал БМ (2), видим, что спектр сигнала БМ отличается от спектра сигнала АМ отсутствием колебания частоты переносчика. На рис. 4 показано произвольный амплитудный спектр модулирующего сигнала и соответствующий ему амплитудный спектр сигнала БМ, состоящий из ВБП и НБП. Из рис. 4 вытекает, что ширина спектра сигнала БМ DF_БМ такая же, как и ширина спектра сигнала АМ: DF_БМ = 2F_max.

2.5 Однополосной называется такой вид модуляции, когда спектр модулированного сигнала совпадает со спектром модулирующего сигнала, сдвинутым на частоту переносчика, или является инверсией сдвинутого спектра относительно частоты переносчика. Спектр сигнала ОМ содержит одну боковую полосу – верхнюю или нижнюю. Сигнал ОМ записывается в виде

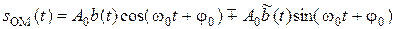, (3)

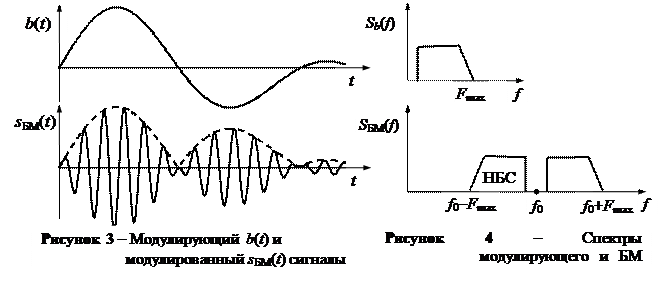где знак “–” относится к описанию сигнала с верхней боковой полосой частот, а знак “+” – с нижней боковой полосой; 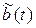– сигнал, сопряженный по Гильберту с сигналом b(t).

Временные диаграммы модулирующего сигнала b(t), сопряженного по Гильберту 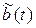и ОМ сигнала приведены на рис. 5. Из рис. 5 видно, что огибающая сигнала ОМ A(t) = A₀ 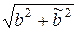(показана пунктирной линией) не повторяет модулирующий сигнал.

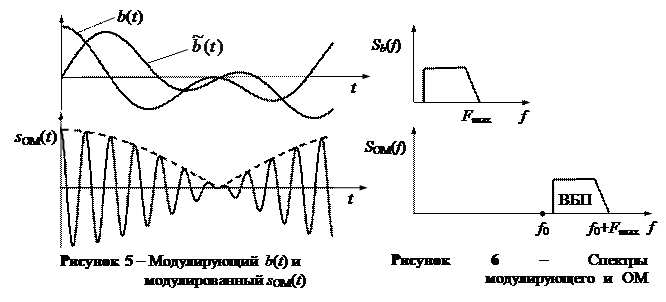
На рис. 6 показано произвольный амплитудный спектр модулирующего сигнала и соответствующий ему амплитудный спектр ОМ сигнала с ВБП. Из рис. 6 вытекает, что ширина спектра ОМ сигнала DF_ОМ вдвое меньше ширины спектра АМ и БМ сигналов: DF_ОМ = F_max.

2.6 Модуляция называется частотной, если приращение частоты переносчика, вызванное модулирующим сигналом, пропорционально мгновенным значением модулирующего сигнала, т.е.

Df (t) = Df_д×b(t), (4)

где Df_д – девиация частоты или максимальное приращение частоты в процессе модуляции.

В это же время имеет место приращение фазы

Dj(t) = 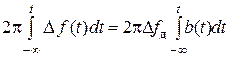. (5)

Математическое описание сигнала ЧМ:

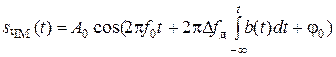. (6)

2.7 Модуляция называется фазовой, если приращение фазы, вызванное модулирующим сигналом, пропорционально мгновенным значением модулирующего сигнала, т.е.

Dj( t) = Dj_д b(t), (7)

где Dj_д – девиация фазы или максимальное приращение фазы в процессе модуляции.

Приращение частоты, которое имеет место в случае фазовой модуляции, определяется выражением

Df(t) = 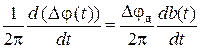. (8)

Временное представление сигнала ФМ:

s_ФМ(t) = A₀ cos(2pf₀ t + Dj_д b(t) + j₀). (9)

2.8 Из приведенных описаний сигналов вытекает, что сигналы ЧМ и ФМ имеют много общего. Как при ЧМ, так и при ФМ имеют место приращения и частоты, и фазы. Название вида модуляции определяется тем, который из параметров получает приращения, пропорциональные модулирующему сигналу.

2.9 Если модулирующий сигнал – гармоническое колебание b(t) = cos 2pFt, то сигнал ЧМ записывается в виде

s_ЧМ(t) = A₀ cos (2pf₀t + m_ЧМ sin 2pFt + j₀), (10)

где m_ЧМ – индекс частотной модуляции, который определяется отношением девиации частоты к частоте модулирующего сигнала

m_ЧМ = Df_д /F. (11)

В случае такого же модулирующего сигнала сигнал ФМ записывается как

s_ФМ(t) = A₀ cos (2pf₀t + m_ФМ cos 2pFt + j₀), (12)

где m_ФМ – индекс фазовой модуляции, который равняется девиации фазы

m_ФМ = Dj_д. (13)

Из сравнения выражений (10) и (12) вытекает, что формы сигналов ЧМ и ФМ совпадают – они лишь взаимно сдвинуты на четверть периода колебания b(t). Как вывод – в случае модуляции гармоническим колебанием и равенства индексов модуляции амплитудные спектры сигналов ЧМ и ФМ одинаковые.

2.10 Для случая модуляции гармоническим колебанием рассмотрим амплитудные спектры сигналов ЧМ и ФМ. Для этого достаточно проанализировать один из видов модуляции, например, ЧМ. Преобразование выражения (10) дает спектральное представление сигнала ЧМ:

s_ЧМ(t) = A₀ J₀(m_ЧМ)×cos 2pf₀t + 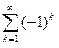А₀J_k(m_ЧМ)×cos(2p(f₀ – k)t) +

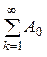+ J_k(m_ЧМ)×cos(2p(f₀ + k)t), (14)

где J_k(m_ЧМ) – значение функции Бесселя первого рода k-го порядка от аргумента m_ЧМ. Графики функций Бесселя приведены на рис. 7.

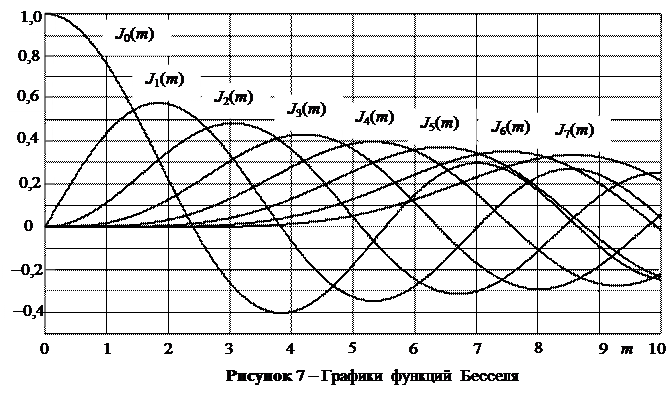Из выражения (14) вытекает, что в спектре сигнала ЧМ есть составляющая на частоте переносчика f₀ (первое слагаемое), ее амплитуда çA₀J₀(m_ЧМ)ç зависит от индекса модуляции m_ЧМ.

Первая сумма в выражении (14) определяет нижнюю боковую полосу с частотами

f_k = f₀ – k, k = 1, 2, 3, ... .

Аналогично, вторая сумма определяет верхнюю боковую полосу с частотами

f_k = f₀ + k, k = 1, 2, 3, ... .

Амплитуды составляющих спектра, размещенных симметрично относительно f₀, для определенного k, определяются как çА₀ J_k(m_ЧМ)ç.

2.11 Из выражения (14) вытекает, что протяженность амплитудного спектра бесконечная. Однако основная часть мощности сигнала сосредоточена в некотором ограниченном частотном интервале вокруг f₀, который и считают шириной спектра сигнала. Если ограничиться учетом составляющих, амплитуды которых не меньше 0,05А₀, то ширина спектра ЧМ сигнала рассчитывается по формуле:

F_ЧМ = 2F (m_ЧМ + 1). (15)

2.12 Изложенное в пп. 2.10 и 2.11 справедливо как для ЧМ, так и для ФМ. Отличие между спектрами ЧМ и ФМ сигналов можно выявить, если зафиксировать параметры модулированных сигналов и изменить частоту модулирующего сигнала. В случае ФМ индекс модуляции m_ФМ остается неизменным и ширина спектра ФМ сигнала по формуле (15) изменяется. В случае же ЧМ индекс модуляции m_ЧМ изменяется согласно формуле (11) и ширина спектра ЧМ сигнала по формуле (15) практически остается неизменной.

2.13 В случае сложных модулирующих сигналов с максимальной частотой спектра F_max ширина спектра модулированного сигнала рассчитывается по формулам

F_ЧМ = 2(m_ЧМ + 1) F_max, (16)

F_ФМ = 2(m_ФМ + 1) F_max. (17)

где индексы модуляции m_ЧМ и m_ФМ определяются соответственно формулами (11) и (13).

2.14 Математические модели сигналов АМ, БМ, ОМ, ЧМ и ФМ в виде соотношений (1), (2), (3), (10) и (12) используются для построения схем формирования и детектирования этих сигналов.

Ключевые вопросы

3.1 С какой целью используется модуляция в системах электросвязи?

3.2 Дать определения амплитудной, балансной, однополосной, частотной и фазовой модуляций.

3.3 Что такое коэффициент амплитудной модуляции? Какие значения он может принимать?

3.4 Что такое преобразование Гильберта?

3.5 Нарисовать временные диаграммы сигналов, когда модулирующим сигналом является гармоническое колебание.

3.6 Изобразить спектры сигналов АМ, БМ и ОМ, когда модулирующим сигналом является гармоническое колебание.

3.7 Изобразить спектры АМ, БМ и ОМ сигналов, когда задан произвольный спектр модулирующего сигнала.

3.8 Объяснить, чему огибающая ОМ сигнала на рис. 5 имеет именно такой вид?

3.9 Пересчитать основные параметры сигналов ЧМ и ФМ, дать их определение.

3.10 Что такое индекс частотной модуляции? Какие значения он может принимать?

3.11 В чем заключается отличие ЧМ от ФМ?

3.12 Как рассчитать спектры ЧМ и ФМ сигналов?

3.13 В спектре сигнала ЧМ (или ФМ), когда модулирующим сигналом является гармоническое колебание, при некоторых значениях индекса модуляции составляющие с частотами f₀ ± F отсутствуют. Чем это объясняется? Каким индексам модуляции это соответствует?

3.14 Частота модулирующего сигнала уменьшилась вдвое. Как при этом изменятся спектры ЧМ и ФМ сигналов?

Домашнее задание

4.1 Изучить разделы “Амплитудная модуляция и ее разновидности” и “Частотная и фазовая модуляция” по конспекту лекций и литературе [1, с. 77...94; 3,с. 149…164; 4,с. 82...103] и описаниям лабораторных макетов в разд. 6.

4.2 Несущее колебание частоты f ₀ модулируется первичным сигналом b(t) = A₁sin(2pf₁t) + A₂sin(2pf₂t) + A₃sin(2pf₃t). Изобразить спектры первичного сигнала и спектры сигналов АМ, БМ и ОМ (положить m_АМ = 1). Исходные данные к задаче согласно номеру Вашей бригады приведены в табл. 1.

Таблица 1 – Исходные данные к домашнему заданию

Номер бригады N	А1, В	f1, Гц	А2, В	f2, Гц	А3, В	f3, Гц	f 0, Гц
	0,3		0,4		0,3
	0,3		0,3		0,4
	0,4		0,3		0,3
	0,3		0,4		0,3
	0,3		0,3		0,4
	0,4		0,3		0,3
	0,3		0,4		0,3
	0,3		0,3		0,4

4.3 Рассчитать амплитудный спектр сигнала ЧМ по таким данным: амплитуда переносчика A₀ = 1 В, частота переносчика f₀ = 2500 Гц; девиация частоты Df_д = 400 + 100N Гц, где N – номер бригады; модулирующим сигналом является гармоническое колебание частоты F = 200 Гц. Результаты расчетов оформить таблицей и построить график спектра. Рассчитать ширину спектра сигнала и показать ее на графике амплитудного спектра.

4.4 Подготовиться к обсуждению по ключевым вопросам.

5 Лабораторное задание

5.1 Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 1.4а Исследование сигналов АМ, БМ и ОМ, используя иконку Лабораторные работы на рабочем столе, а затем папки ТЭСи Модуль 1. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.2 Провести исследование модулированных сигналов во временной и частотной областях.Для этого:

– установить значения A₁, f₁, A₂, f₂, A₃, f₃, коэффициент m_АМ и частоту f ₀ такие же, как и в домашнем задании;

- установить вид модуляции АМ и запустить программу на выполнение;

- зарисовать в протоколе осциллограммы и спектрограммы сигналов на входе и на выходе модулятора;

- установить поочередно виды модуляции БМ, ОМ из ВБС, ОМ из НБС, после выполнения программы зарисовать в протоколе спектрограммы сигналов на выходе модулятора;

- сравнить рассчитанные в домашнем задании и полученные на компьютере спектрограммы, результаты сравнения занести к выводам протокола;

- сделать выводы относительно соответствия форм модулирующего сигнала и огибающей модулированного сигнала для разных видов модуляции.

5.3 Провести исследование спектров модулированных сигналов в случае изменения частоты несущего колебания.Для этого сначала увеличить на 200 Гц, а затем уменьшить на 200 Гц частоту несущего колебания, зарисовать в протоколе полученные на выходе модулятора спектрограммы сигналов. Изменения в спектрограммах в сравнении с полученными в п. 5.2 занести к выводам протокола.

5.4 Провести исследование сигнала ОМ в случае однотонального модулирующего сигнала.Для этого:

– установить значения A₁ = 1 В, f ₁ = 100 Гц, A₂ = A₃ = 0, частоту f ₀ такую же, как и в домашнем задании;

– установить вид модуляции ОМ с ВБП, а затем ОМ с НБП;

– зарисовать в протоколе осциллограммы и спектрограммы сигналов b(t), 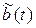и s_ОМ(t);

– сделать выводы относительно соответствия сигналов b(t), 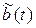, s_ОМ(t) и огибающей модулированного сигнала A(t) = A₀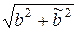

5.5 Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 1.4б Исследование сигналов ЧМ и ФМ, используя иконку Лабораторные работы на рабочем столе, а затем папки ТЭСи Модуль 1. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.6 Провести исследование амплитудного спектра сигнала ЧМс параметрами, которые использованы в домашнем задании. Для этого следует на вход модулятора подать гармоническое колебание, установить его частоту и девиацию частоты. Зафиксировать в таблице значения частот и амплитуд составляющих. Построить график амплитудного спектра. Сравнить его со спектром, рассчитанным в домашнем задании. Сделать вывод об их совпадении.

5.7 Провести исследование амплитудного спектра сигнала ФМс девиацией фазы, равной индексу ЧМ в п. 5.6, и при таком же модулирующем колебании. Зафиксировать в таблице значения частот и амплитуд составляющих. Построить график амплитудного спектра. Сравнить его со спектром, полученным при выполнении п. 5.6. Сделать вывод об их совпадении.

5.8 Провести исследование амплитудного спектра сигнала ЧМ, когда модулирующий сигнал – сложное колебание (сумма гармоничных колебаний с частотами 70 и 200 Гц). Установить значение девиации частоты 600 Гц. Зафиксировать в протоколе в виде эскиза график амплитудного спектра. Оценить ширину спектра сигнала, как протяжность полосы частот, где амплитуды составляющих не меньше 10 % от наибольшей амплитуды составляющей в спектре сигнала. Рассчитать ширину спектра сигнала по формуле (16) и сравнить ее с определенной экспериментально.

5.9 Провести исследование амплитудного спектра сигнала ФМ, когда модулирующий сигнал – сложное колебание (сумма гармоничных колебаний с частотами 70 и 200 Гц). Установить значение девиации фазы Dj_д = 3. Зафиксировать в протоколе в виде эскиза график амплитудного спектра. Оценить ширину спектра сигнала, как протяженность области частот, где амплитуды составляющих не меньше 10 % от наибольшей амплитуды составляющей в спектре сигнала. Рассчитать ширину спектра сигнала по формуле (17) и сравнить ее с определенной экспериментально.