Поля точкового заряду та системи точкових зарядів

7.1 Мета роботи

Ознайомитись із графічним зображенням електричного поля точкового заряду та системи точкових зарядів за допомогою електричних силових ліній поля та дослідити особливості їх побудови.

7.2 Вказівки до організації самостійної роботи

Важливим поняттям електростатики є поняття точкового заряду. Точковими зарядами називають заряджені тіла, розміри яких малі порівняно з відстанню між ними. Кожен заряд створює електричне поле у навколишньому просторі. Важливою характеристикою електричного поля є вектор напруженості поля . Поле будь-якого електричного заряду або системи зарядів можна описати графічним способом за допомогою ліній напруженості, які скорочено називають лініями або силовими лініями поля. Лінії напруженості проводять так, щоб кількість ліній, які пронизують одиницю поверхні, перпендикулярно до площини поверхні, дорівнювала числовому значенню вектора . Тоді за картиною ліній напруженості можна судити про напрямок та величину вектора в різних точках простору.

Лінії поля точкового заряду q є сукупністю радіальних прямих, які виходять із позитивного заряду або входять в негативний заряд.

Для точкового заряду напруженість поля в будь-якій точці у вакуумі визначається формулою [2, 5]:

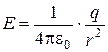, (7.1)

де 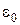− електрична стала, r – відстань між зарядом та точкою спостереження.

Повна кількість ліній N, які перетинають сферичну поверхню довільного радіусу r, називають потоком вектора . Воно дорівнюватиме добутку густини ліній на величину площі поверхні сфери 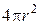. Густина ліній, згідно з умовою, дорівнює

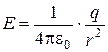. (7.2)

Отже, кількість ліній N або потік вектора крізь замкнуту поверхню, яка охоплює заряд, чисельно дорівнює

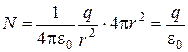. (7.3)

Це твердження є змістом теореми Гаусса для вакууму [2, 5].

Отриманий результат означає, що кількість ліній на будь-якій відстані від заряду буде така сама. Звідси випливає, що силові лінії можуть починатися на заряді і закінчуватися на заряді, або прямувати в нескінченність. Картина силових ліній точкового заряду в площині, що включає заряд, буде подібною картині ліній для заряду, розподіленого вздовж тонкої нитки з деякою густиноюτ в площині, перпендикулярній нитці. Для зарядженої нитки у вказаній площині напруженість поля визначається формулою

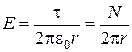, (7.4)

а кількість ліній , які перетинають коло радіуса r, тоді дорівнюватиме:

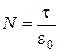. (7.5)

Порівнюючи вирази (7.3) та (7.5) бачимо, що немає значення, чи будемо ми вивчати поле в площині, що створює точковий заряд або систему точкових зарядів, які знаходяться в одній площині, чи поле в площині, перпендикулярній нитці або системі заряджених ниток. Картина силових ліній точкового заряду в площині, в якій розміщується заряд q буде такою самою, як і для заряду, розподіленого вздовж тонкої нитки з лінійною густиною, що чисельно дорів-
нює заряду q: τ = q. Внаслідок доказаної еквівалентності далі ми вживатимемо термін − точковий заряд.

7.3 Опис комп’ютерної програми

Зовнішній вигляд інтерфейсу програми зображено на рис. 7.1. Програма будує силові лінії електричного поля в двовимірному випадку за алгоритмом:

1. Вибирається точка з координатами (х, у) і обчислюються компоненти поля .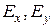

2. Проводиться в цій точці невеликий прямолінійний відрізок 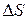у напрямку вектора .

3. Процедура повторюється з нової точки ( 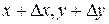). Процес продовжується доти, доки силова лінія не йде в нескінченість, або до будь-якого негативного заряду. Кількість силових ліній, які починаються біля кожного позитивного заряду, пропорційна величині заряду. Величина заряду вибирається в умовних одиницях.

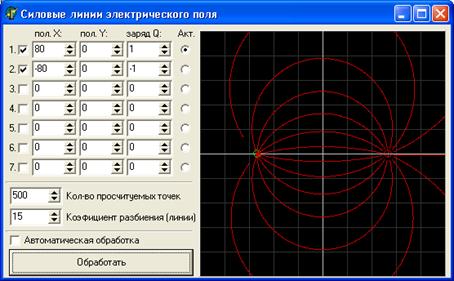
Рисунок 7.1

7.4 Інструкція користувачу

1. Помістіть в точку з координатами 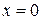, 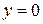точковий заряд q (величину q взяти з табл. 7.1). Виберіть число ліній 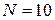, число кроків (яке визначає довжину силових ліній на екрані) підберіть так, щоб вони охоплювали весь екран. Зарисуйте картину поля.

2. Збільшіть заряд вдвічі. У скільки разів треба збільшити число N, щоб за графічним зображенням поля можна було визначити величину напруженості?

3. Виберіть на картині поля замкнену лінію довільної форми. Підрахуйте число ліній, які входять в площину, охоплену лінією (потік, який входить), число ліній, які виходять назовні 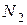(потік, що виходить). Чому дорівнює потік, який перетинає замкнену лінію?

4. Розмістіть два однакових заряди на відстані 2-х клітинок (величину q взяти з табл. 7.1). Отримайте для них картину силових ліній, зарисуйте її.

5. Отримайте картину силових ліній для системи двох однакових зарядів протилежного знаку. Зарисуйте її.

6. Помістіть заряд величиною 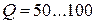умовних одиниць в точку з координатами 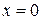, 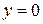. Внесіть в поле цього заряду невеликий пробний заряд q (згідно з табл. 7.1). Змінюючи його положення відносно Q, зробіть висновок, наскільки сильно він викривлює картину поля. Повторіть операції для негативного заряду –q.

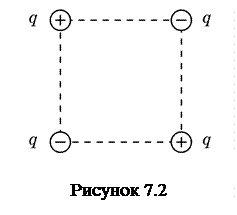7. Розмістіть у вершинах квадрата заряди однакової величини за схемою (рис.7.2) – така система носить назву – квадруполь. Отримайте картину силових ліній та зарисуйте її. Які особливості має картина поля квадруполя?

Таблиця 7.1 – Вихідні дані

Номер

q

N

7.5 Зміст звіту

Звіт має містити: мету роботи, якісні зарисовки картин поля, утворених одним, двома точковими зарядами, диполем, квадруполем (пункти 1, 4, 5, 7), висновки за пунктами 3, 6, 7.

7.6 Контрольні запитання і завдання

1. Дайте визначення силової лінії поля.

2. Що характерно для силових ліній електростатичного поля ?

3. Нарисуйте лінії електричного поля для точкового позитивного, негативного заряду.

4. Запишіть формулу, яка визначає напруженість точкового заряду.

5. Як пов’язаний потік вектора з повним числом силових ліній, що виходять з заряду (або входять у заряд)?

6. Сформулюйте теорему Гаусса. Що таке диполь?

7. Яку систему зарядів називають квадруполем?