Движение ракеты с переменной массой
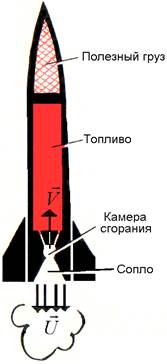 | Рассмотрим движение ракеты, рисунок 1. Пусть к некоторому моменту времени t масса ракеты с топливом равна m, скорость её движения относительно Земли V, скорость вылета продуктов сгорания топлива относительно ракеты U. Тогда импульс ракеты в данный момент времени равен 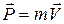 . К моменту времени t + dt в процессе сгорания топлива массой dm скорость ракеты увеличилась и стала равной V + dV, а масса ракеты уменьшилась на dm и стала равной m - dm. Импульс ракеты и топлива к данному моменту времени может быть определен по формулам . К моменту времени t + dt в процессе сгорания топлива массой dm скорость ракеты увеличилась и стала равной V + dV, а масса ракеты уменьшилась на dm и стала равной m - dm. Импульс ракеты и топлива к данному моменту времени может быть определен по формулам 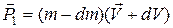 , , 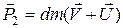 . При этом абсолютная скорость движения топлива, т.е. скорость вылета продуктов сгорания топлива из ракеты относительно Земли . При этом абсолютная скорость движения топлива, т.е. скорость вылета продуктов сгорания топлива из ракеты относительно Земли 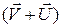 . . |
| Рисунок 1 - Схема ракеты |
Изменение импульса за промежуток времени dt равно
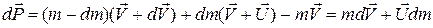 . (1)
. (1)
(величиной второго порядка малости dmdV пренебрегаем).
По второму закону динамики действующая сила равна скорости изменения импульса
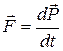 . (2)
. (2)
Подставляя (2) в (1), получим
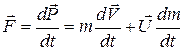 . (3)
. (3)
Для изолированной системы внешняя сила равна нулю, поэтому уравнение (3) будет иметь следующий вид:
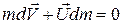 . (4)
. (4)
Решим полученное дифференциальное уравнение методом разделения переменных.
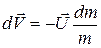 . (5)
. (5)
Проинтегрируем соотношение (5).
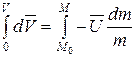 , (6)
, (6)
где M0 - начальная масса полностью снаряженной топливом ракеты (масса ракеты вместе с топливом); M0 = МТ + Мп. (где Мп - полезная масса ракеты, масса ракеты без топлива).
M - текущая (в данный момент времени) масса ракеты с оставшейся массой топлива.
Учитывая, что dM - величина отрицательная, численное значение скорости движения ракеты определится после интегрирования (6).
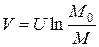 . (7)
. (7)
Полученное уравнение (6) называется уравнением Циолковского.
Масса топлива сгоревшего при движении ракеты может быть определена по формуле
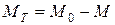 . (8)
. (8)
Из данных компьютерного эксперимента, можно построить зависимость M = m(t) (рисунок 2).
Скорость расхода (сгорания) топлива Uтоп:
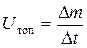 . (9)
. (9)
Следовательно, по тангенсу угла наклона зависимости M = m(t), (участок графика до tС, где tС – время сгорания топлива) можно определить скорость сгорания топлива.
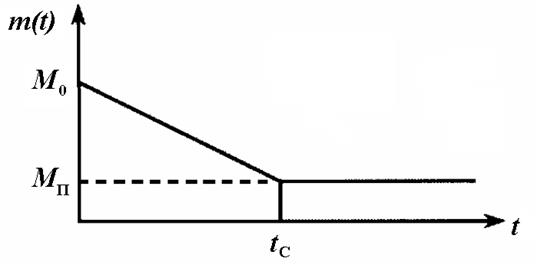 |
| Рисунок 2 - Зависимость массы ракеты от времени |
Если скорость движения ракеты относительно Земли достигнет значения примерно 7,9 км/с, то ракета будет двигаться по круговой орбите. Эта скорость называется первой космической. Если скорость ракеты будет равна или больше 11,2 км/с, то ракета может преодолеть гравитационное притяжение Земли и стать спутником Солнца (вторая космическая скорость). В том случае, когда скорость ракеты достигнет 16,7 км/с (третья космическая скорость), ракета, преодолевая притяжение Солнца, покинет Солнечную систему.
Путь S, который проходит ракета можно определить по формуле
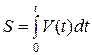 . (10)
. (10)
Компьютерный эксперимент
Компьютерный эксперимент позволяет изменять количество топлива, помещенного в ракету, определять максимальную скорость ракеты. Компьютерная программа предусматривает графический вывод на монитор зависимости скорости движения ракеты от времени V = f(t), а также значение максимальной скорости ракеты. Кроме этого в пошаговом режиме на экран выводится информация о массе ракеты в данный момент времени.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
1. Компьютер.
2. Программа «Открытая физика 1.1» ООО «Физикон».
