Дифракция Фраунгофера на одной щели
Пусть имеется узкая длинная щель шириной а =АВ (Рис. 1.22). На нее падает пучок параллельных лучей.
 |
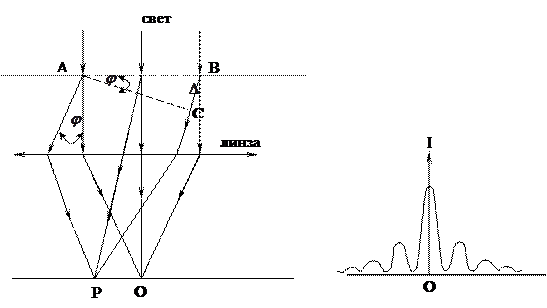Рис. 1.22
На рисунке АВ - плоский фронт падающей волны. Каждую точку этого фронта согласно принципу Гюйгенса рассматриваем как источник вторичных волн. АС-фронт дифрагированной волны. Пусть лучи, идущие под углом φ к первоначальному направлению, соберутся в точке Р. Определим амплитуду колебаний в этой точке.
Рассмотрим фазовые соотношения отдельных колебаний в точке Р от различных точек плоской волновой поверхности. Пусть начальная фаза колебаний от точки А равна α1, а от точки В- α2. Разность хода Δ лучей, приходящих от этих точек в точку Р:
Δ=ВС= аsinφ
но т.к.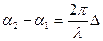 
, то
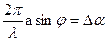(1.38)
Предложим теперь, что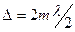 
, тогда волновую поверхность можно разделить на четное число 2m зон Френеля, колебания от которых проходят в точку Р в противоположных фазах и ослабляют друг друга (см. Рис. 1.22). Таким образом, если на ширине щели “a” укладывается четное число зон Френеля, т.е.
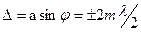(1.39)
то в точке Р будет минимуминтенсивности света. Если ширина щели «a» такова, что на ней укладывается нечетное число зон, т.е.
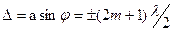(1.32)
то в точке Р будет максимум.
Если φ=0, то Δα=0, т.е. колебания от всех точек открытой волновой поверхности АВ происходят в одной фазе и поэтому в точке О будет наблюдаться центральный максимум (максимум нулевого порядка).
Можно определить углы φ, под которыми будут рассматриваться максимумы и минимумы, пользуясь условиями (1.39) и (1.40).
Определим также ширину центрального максимума (нулевого порядка). Он располагается между двумя симметричными минимумами первого порядка:
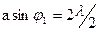(m=1)
Тогда 
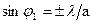
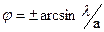или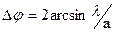 
При λ<<a
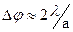(1.41)
т.е. чем уже щель (меньше a), тем дальше друг от друга располагаются максимумы и минимумы, шире будет дифракционная картина.
Если щель освещать немонохроматическим светом, то максимумы будут иметь радужную окраску (при этом из 1.41) можно заключить, что цветам с большей длиной волны λ (красный в видимой области) будут соответствовать и большие углы φ.