Энергия дискретизированной функции

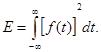
Теорема Парсеваля, позволяет утверждать, что среднеквадратичное значение f(t) равно сумме квадратов абсолютных значений коэффициента разложения этой функции в ряд Фурье.

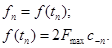
Заменим f(t) на решетчатую функцию :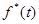

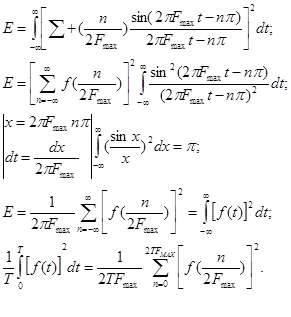
27.Квантование сигналов.

После квантования сигнал может принимать ограниченное число состояний или отчётливых различных сигналов.

Характеристика квантования:

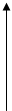y

X

Если ступенчатая функция характеризуется одинаковой величиной ступенек, то такая характеристика называется регулярной. Если ступени неодинаковые, то нерегулярной. Характеристика квантователя меняется во времени. При квантование имеется опасность появления флуктуации – выходного сигнала при переходе от одной ступени к другой, из за нечастого квантования (шум-квантования).

Квантование является нелинейной операцией. Точность зависит от того, насколько мала ступень квантования.

Ошибка квантования e(t)- функция элементарного уровня, она не может превышать значение q, её можно рассмотреть как шум; 0 .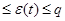

Частота квантования связана с x(t), которая в свою очередь связана с частотой сигнала в этом спектре.

e(t) может рассматривать как последовательность отрезков, с переменной амплитудой ±q+2.

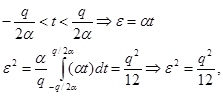
где a-переменная крутизна.

Чем меньше ступень квантования, тем меньше шум.

28.Способы квантования сигналов.

Если входной сигнал в процессе передачи изменяется таким образом, что эффективно используемое число ступеней квантования уменьшается, то выгодно сжать элементарные уровни при изменении сигнала с малыми амплитудами и расширить эти же уровни для сигналов с большими амплитудами.

Элементарный уровень следует закону:

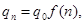где f(n)-функция повторения, которая определяется таким образом, чтобы оптимизировать процесс передачи.

Данная операция квантования получила название – динамическое амплитуда.

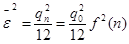-шум квантования.

В случае логарифмического квантования интервал квантования q, является функцией порядкового уровня определяемого выражением:

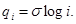
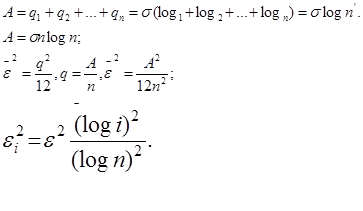
Такое квантование позволяет улучшить передачу кодированного сигнала без увеличения уровней квантования, при этом значительно улучшается качество сигналов низкого уровня.

29.Аналого-цифровое преобразование сигналов (характеристики).

Скорость дискретизации.

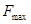-наибольшая частота кодируемого сигнала. n-число цифр кода (разрядность), то наименьшая частота следования кодовых импульсов без учёта сигналов синхронизации - .

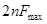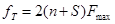-тактовая частота.

S-число импульсов синхронизации.