ВЕРОЯТНОСТЬ ПЕРЕПОЛНЕНИЯ БУФЕРА. Ро = Рхх ρ = λТо – коэффициент загрузки

Ро = Рхх ρ = λТо – коэффициент загрузки

По каждому каналу буфер имеет память объемом N.

Достаточно небольшого разброса коэффициента загрузки и вероятность опустошения меняется очень здорово.

ρ = λ/Fo

Вероятность потери существующего отсчета (вероятность переполнения буфера)

Берем m тактов: mTo – интервал времени.

Рпотр = lim màώ

Рпотр = 1 -

ДОПОЛНИТЕЛЬНЫЙ ВОПРОС:

Вывод этого выражения 1-ρо – вероятность того, что в буфере что-то есть.

Кривые вероятности потери:

Потеря одиночной выборки не приводит к фатальным последствиям при передаче аналоговой информации(температура и др) Предпочтительнее коэффициент загрузки 0.95, взять N=100, можно получить низкие вероятности потери, но увеличиться вероятность холостого хода(но это ничего страшного)

Рассматриваем интервал (KTo, (K+1)To); KTo=<t<(К+1)To

Pλ – выход в радио линию

Наши отчеты имеют случайную задержку, которая состоит из задержек на целое число тактов, и на некоторую случайную задержку:

τз = Кто + τ , где τ – случайная величина(задержка)

к – случайная величина

кТо определяется состоянием БЗУ (величиной очереди), вероятностью Рj

W(τз) = =

P₁(t) = P₂e^-λt + λt P₁ + λt P₀e^-λt

Pj(t) = _+1-j e^-λt + Po^-λt

0 j < N

Вероятность того, что в БЗУ будет 1 выборка, равна вероятности трех несовместимых событий. В БЗУ было в интервале предшествующий тактовому интервалу 2 выборки одна вышла, одна осталась; в БЗУ был 1 существенный отсчет один вывели, один поступили, в БЗУ не было ни одного отсчета, один поступил после момента кТо

Можно получить среднее значение(математическое ожидание) и дисперсию задержки:

М(τз) = То/2 + - - M²(τз)

Задержку в целое число тактов можно учесть, а задержку внутри такта принудительно учесть нельзя, так как она случайная величина.

Ошибки восстановлены, обусловленные процедурой электрополяции задержкой и потерей выборки.

В приемной части системы перед нами стоит следующая задача: есть параметр S(t) который представлен существенными отсчетами.

S(t) – истинное значение

S*(t) – оценка

ЛЕКЦИЯ №7

Полагаем, что процесс у нас гаусовский с дисперсией δ²с. Процесс дифференцируемый и в пределах апертуры можно аппроксимировать его прямой с наклоном θ, где θ – производная нашего случайного(гаусовского) измеряемого процесса.

Таким образом можем записать выражение для ошибке:

Z²(t)= ( );

ξ²= =D²/12 δ²с(1+12Рпот + 6πλ δτ²) (1) относительная ошибка

Из теорем случайных процессов:

θ²= δ²сω₁²; λ= ;

Кроме этого, можно также вычислить ошибку, обусловленную задержкой и экстраполяцией. Из теории известно, что ошибка экстраполяции и ошибки равны:

ошибка экстраполяции

- ошибка, обусловленная потерей

И учитывается такой факт, что ошибка обусловленная потерей существует относительное время равное 2Рпот. И тогда, у нас получается:

Рпот – ошибка чисто обусловленная потерей

В выражении (1)

1–е слагаемое - ошибка, обусловленная экстраполяцией

2-е слагаемое - ошибка обусловленная потерей

3-е слагаемое - ошибка, обусловленная задержкой

Ошибка задержки определяется дисперсией задержки и интенсивностью существенных отсчетов( чем больше интенсивность, тем больше задержек)

То, что мы рассматриваем, нужно относить к сжатию с потерями(используется при аналоговой информации)

Принципиально под сжатием без потерь понимают оптимальные передачи информации или передачу информации с предсказанием.

Хз=Хз-Хзn – передается разница – это оптимальная передача (увеличивается скорость передачи информации, уменьшается кодовая последовательность)

При передаче аналоговой информации можно сначала использовать сжатие с потерей, а затем сжатие без потерь(это более эффективно)

Билет № 14. Системы синхронизации цифровых РТС передающая часть

Система синхронизации цифровой РТС Передающая часть

С.С. – сигнал синхронизации слов

Это формирует УСС – устройство управление синхронизацией.

Рассматриваем равномерный циклический опрос система последовательная

Приемная часть

I – аппаратная часть, II – программная реализация

Оптимальный приемник и хороший демодулятор нуждается в тактовой синхронизации.

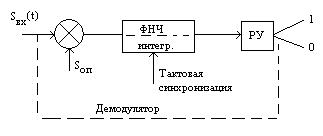Тактовая синхронизация - это определение границ сигнала прием, оптимальный, когда фазовый детектор и тактовая синхронизация имеют перекрестные связи.

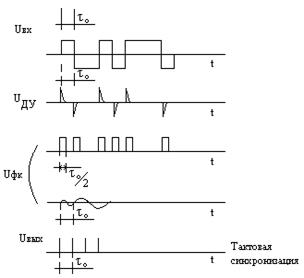На входе блока тактовой синхронизации мы имеем последовательность нулей и единиц, из которых надо выделить сигнал тактовой синхронизации.

Блок тактовой синхронизации.

(-) Но возникает принципиальный вопрос: по тем или иным причинам тактовая частота может сдвигаться, из-за этого затрудняется фильтрация, нужен узкополосный следящий фильтр. Этот сдвиг не может учитываться при формировании τ₀/2. Принципиально получится ошибка при формировании сигнала тактовой синхронизации.

Расщеплять фазу надо в передатчике.

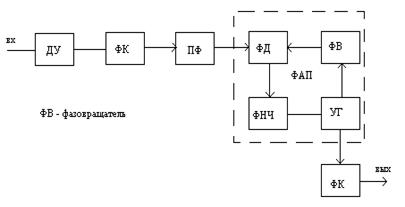
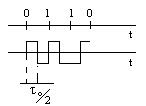
В этом случае такой ошибки нет.

ЛЕКЦИЯ № 12

Во 2-м варианте, когда используется двоичный код с расщепленной фазой, этот вариант обладает более высокими синхросвойствами по сравнению с 1-м, т.к. всем возможным сдвигом по частоте и фазе подвергается сигнал тактовой синхронизации на выходе приемника демодулятора(То/2 изменяется из-за этих факторов), в 1-ом варианте То/2 формируется в приемнике и эти сдвиги не учитываются.

Блок тактовой синхронизации слов.

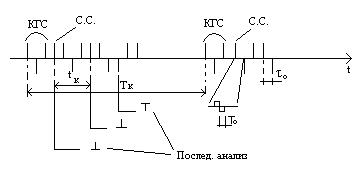
Можно выделить 2 способа:

1. Послед. Анализа

2. Параллельного анализа

n – объем анализа(количество прошедших слов)

Последовательный метод не является оптимальным с точки зрения времени поиска. Достаточно просто предложить устройство или алгоритм, который позволит за интервал времени равный длительности слова, выделить импульс(сигнал), который соответствует сигналу синхронизации слова (сигнала слова).

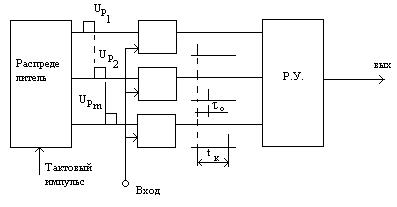
Решающее устройство содержит:

- обнаружитель единиц,

- счетчик на заданном интервале,

- схему критерия решения.

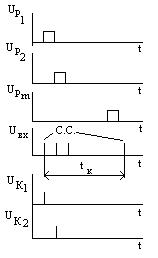Всегда существует вероятность того, что на заданном объеме анализа МП накопим по каналу большее число, чем порог решающего устройства при равномерном потоке нулей и единиц. Получим следующий результат:

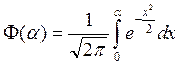
Рош=(m-1)[0.5 – Ф( )]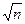

N
Рош	3*10-2	3*10-4	3*10-6	3*10-7

Робн =0,99 – вероятность обнаружения единиц,

Рнеобн =0,01 – вероятность обнаружения нулей

При m=10 (длина слова):

Робн ≥0,99,

Рнеобн ≤0,01

Распределение нулей и единиц на интервале равновероятно. Даже при большом объеме (n=30) вероятность ошибки довольно большая.

Есть проблема выбора порога (очень жесткий порог плохо ставить, можно пропустить сигнал синхронизации).

ЛЕКЦИЯ №13