Розрахунок характеристик аналого-цифрового перетворення та інформаційних характеристик повідомлень на виході АЦП

Визначимо мінімально допустиме число рівнів квантування L, значність кодових комбінацій та тривалість символу на виході АЦП, вважаючи, що тривалість кодової комбінації дорівнює інтервалу дискретизації. Верхня гранична частота спектру повідомлення F_max = 4,3 кГц, пікфактор сигналу П = =25 дБ, допустиме відношення сигнал/завада квантування р_kb = Р_b/Р_e = 43 дБ.

Для розрахунків використовуємо оцінку величини <e²(t)> – средньої потужності шуму квантування, яка дорівнює <e² (t)> =D²/12. Тоді:

P_B/P_e = <B²(t)>/< e²(t)> = 12 <B²(t)>/ D².

Вважаючи, що B(t) – нормоване повідомлення –1 < B(t) < 1 отримаємо

D = (B_max– B_min)/(L–1) = 2/(L–1).

З іншого боку P_B = <B²(t)> = 1/ П², де П – пікфактор сигналу. Отже

P_B/P_e = <B²(t)>/< e²(t)> = 12 / (П² D²) = 3(L–1)²/ П²,

звідки кількість рівнів квантування:

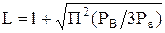(2.1)

В цій формулі співвідношення сигнал-завада і пікфактор сигналу задані у відносних одиницях тому їх необхідно перетворити, поклавши:

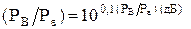і П = 10^{0,1×П (дБ)}.

Кількість рівнів квантування остаточно

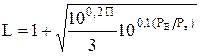
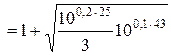» 2,58.10⁴.

Значність кодових комбінацій n знайдемо як

n ³ log₂ L » 1,443×ln L = 1,443×ln 2,58.10⁴ = 14,66.

Округлимо отриману величину до найближчого більшого цілого і приймемо n= =15. Скоректоване значення кількості рівнів квантування L = 2ⁿ = 2¹⁵ = 32768.

Тривалість кодової комбінаціі дорівнює інтервалу дискретизації, а він згідно теореми Котельникова становить Т_д = 1/(2f_в), де f_в - верхня гранична частота спектру первинного сигналу. Отже: Т_д = 1/(2f_в) = 1/(2×4,3) = 0,116 мс.

Тривалість символу кодової комбінації на виході АЦП

t_с = Т_д/n = 0,116/15 = 0,00775 мс = 7,75 мкс.

Ентропіянезалежних дискретних повідомлень на виході АЦП та продуктивність джерела повідомлень, якщо імовірність передачі символу 1: Р(1) = 0,К = 0,1 де К = 1.

Середнє значення кількості інформації в одному квантованому відліку Н_від(А) (ентропія відліку) обчислюється як математичне очікування кількості інформації:

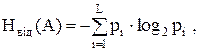(2.1)

де L – число рівнів квантування; р_і – iмовiрнiсть появи у квантованому повідомленні і – го рівня. Для L рівноімовірних рівнів квантування імовірність кожного з них р_і = 1/L. Тому для нашого випадку ентропія джерела незалежних повідомлень за формулою (2.1) буде:

Н(А) = –log₂(1/L) = –log₂(1/32768) = 15 біт/пов.

Для двійкового джерела при рівноімовірних символах 1 і 0 ентропія буде максимальною Н_max(А) = log₂ 2 = 1 біт/пов. При різних імовірностях символів, наприклад, якщо згідно завданню Р(а₁) = р = 0,1 і, відповідно, Р(а₂) = 1 – р = 0,9, згідно з формулою (2.1) для двійкового джерела отримуємо:

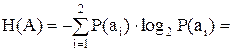–p log₂p – (1 – p) log₂(1 – p) =

= – 0,1 log₂ 0,1 – 0,9 log₂ 0,9 = – 0,1×1,443×ln 0,1 – 0,9×1,443×ln 0,9 =

= – 0,1×1,443×(–2,3) – 0,9×1,443×(–0,11) = 0,33+0,14 = 0,47.

Для обчислення двійкових логарифмів користуємось математичним правилом: log₂ z = ln z/ln 2 » 1,443 ln z.

Продуктивність джерела. Під продуктивністю джерела розуміють середню кількість інформації, утвореної джерелом за одиницю часу. Для неперервних повідомлень у разі їх перетворення в цифрову форму з частотою дискретизації f_д та ентропією відліків Н_від(А) продуктивність джерела може бути обчислена за формулою

R_дн = f_д Н_від(А). (2.2)

Для L рівноймовірних рівнів квантування ймовірність кожного з них р_і = =1/L, і з формул (2.1) та (2.2) дістаємо, що максимальне значення продуктивності джерела неперервних повідомлень

R_дн = f_д log₂ L = 2×4,3×10³×15 = 1,29×10⁵ біт/с.

Для двійкового джерела дискретних повідомлень

R_дд = Н(А) / t_с = 0,47×/ 7,75×10^-6 = 6,1×10⁴ біт/с.

В даному випадку за умовами задачі маємо не надто велике значення ентропії джерела за рахунок невеликої імовірності появи у двійковому повідомленні символу 1 (потік двійкових символів складається переважно з нулів). Це обумовлює відносно невисоку продуктивність джерела.