Электрооптические модуляторы

Электрооптические модуляторы нашли широкое применение в системах лазерной связи. Они характеризуются следующими положительными факторами: а) на основе электрооптического эффекта можно реализовать все рассмотренные методы модуляции, б) возможна широкополосная модуляция, в) спектральный диапазон по несущей включает весь оптический диапазон, г) электрооптические кристаллы не очень дороги, и модуляторы просты по конструкции.

а) Электрооптический модулятор интенсивности излучения

Схема, поясняющая принцип действия электрооптического модулятора интенсивности излучения, показана на рис. 2.

Рис. 2

Луч лазера интенсивности линейно поляризуется под углом 45⁰ по отношению к эллипсоиду коэффициентов преломления

кристалла. Анализатор, следующий за модулятором, ориентируется

ортогонально поляризации излучения лазера. Таким образом, если к кристаллу электрическое поле не приложено, то луч лазера полностью ослабляется модулятором. Состояние поляризации лазера, ячейка Поккельса и анализатор могут быть представлены поляризационными матрицами, отнесенными к кристаллическим осям.

Матрицы поляризации луча лазера имеет вид

Модулятор с полной фазовой задержкой характеризуется операционной матрицей

Матричный оператор анализатора

Матрица поляризации луча на выходе модулятора

Эта матрица характеризует линейно-поляризованный свет под углом –45⁰ по отношению к оси кристалла модулятора. Амплитуда

Электрического поля светового излучения пропорциональна sinГ/2.

Мнимая единица i соответствует фазовому сдвигу, на 90⁰ обоих

Компонент электрического поля X` и Y`, входящих в модулятор,

В данном случае это обстоятельство не оказывает влияния на последующие выкладки. Интенсивность излучения на выходе модулятора

где 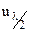- полуволновое напряжение модулятора.

На рис. 3 графически показана зависимость между отношением выходной интенсивности излучения ко входящей в модулятор и фазовым сдвигом (модуляционная характеристика).

Рис.3.

Т.к. фазовая задержка пропорциональна модулирующему напряжению, то в первом случае выбора рабочей точки (рис. 3а) наблюдаются значительные искажения. Искажения могут быть сведены к минимуму установкой рабочей
точки модулятора на линейном участки модуляционной характеристики (рис. 3б) и при ограничении амплитуды управляющего напряжения величиной 0,25 . Снимки реальных осциллограмм сигналов и их спектров, соответствующих положению рабочей точки 1,2 и 3, приведены на рис 4а, 4б и 4в – соответственно.

	Рис.4а.

	Рис.4б.

	Рис.4в.

Рабочая точка модулятора может устанавливаться подачей на кристалл постоянного напряжения (электрическое смещение), которое вносит четвертьволновую фазовую задержку Г= /2 (в отсутствие модулирующего напряжения). Практически более конструктивным решением этого вопроса является применение четвертьволновой оптической пластины (оптическое смещение). Пластина устанавливается до или после ячейки Поккельса. Операционная матрица пластины, вносящей фазовую задержку в четверть длины-волны /2 имеет вид

Тогда результирующая поляризационная матрица на выходе модулятора

Интенсивность излучения на выходе модулятора становится равной

Таким образом, при отсутствии модулирующего напряжения интенсивность излучения на выходе модулятора равна половине интенсивности излучения на входе. В электрооптических кристаллах фазовая задержка линейно зависит от приложенного напряжения. Для приложенного синусоидального модулирующего напряжения фазовая задержка может быть записана в виде

Г = k_mu_msin t

где k_m - постоянная пропорциональность,

u_m - максимальное модулирующее напряжение и

- частота модуляции.

Тогда интенсивность на выходе модулятора

Это уравнение может быть записано с применением функций Бесселя первого рода

Таким образом, на выходе модулятора имеем постоянную составляющую с интенсивностью, равной ½ интенсивности излучения на входе модулятора, гармоническую составляющую основной частоты с относительной амплитудой и высшие основной частоты. Гармоники основной частоты. Высшие гармонические составляющие характеризуют искажения модуляционного процесса. Величина искажений D_i определяется отношением корня квадратного из суммы квадратов амплитуд гармоник к амплитуде основной гармоники

Коэффициент глубины модуляции определяется

Если необходимо получить модуляцию, близкую к 100% нужно учитывать, что в этом случае третья и высшие гармонические составляющие становятся большими и, следовательно, искажения увеличиваются.