Задача 1. 1. Тангенс угла диэлектрических потерь:
1. Тангенс угла диэлектрических потерь:

где  – удельная электрическая проводимость,
– удельная электрическая проводимость,  – угловая частота,
– угловая частота, 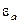 – абсолютная диэлектрическая проницаемость.
– абсолютная диэлектрическая проницаемость.
Если в среде 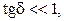 то ее называют диэлектриком, если
то ее называют диэлектриком, если 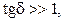 то среду называют проводником.
то среду называют проводником.
При значениях  среда является полупроводящей.
среда является полупроводящей.
2. Выбор формул для расчета параметров волны определяется значением 
при 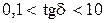

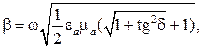
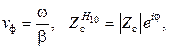
где 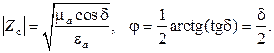
При значениях  или
или 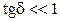 следует использовать упрощенные формулы:
следует использовать упрощенные формулы:
при 
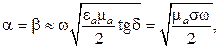

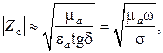
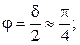
при 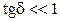
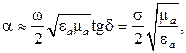


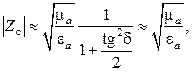
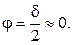
Для всех сред коэффициент распространения и длина волны определяются выражениями:
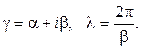
3. При построении зависимости структуры поля волны от координаты z необходимо учесть, что в среде без потерь колебания векторов 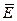 и
и 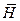 происходят в одной фазе (рис. 1), в среде с потерями между векторами
происходят в одной фазе (рис. 1), в среде с потерями между векторами 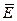 и
и 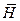 имеется фазовый сдвиг (рис. 2).
имеется фазовый сдвиг (рис. 2).

Рис. 1

Рис. 2
