Молекулярно-кінетична теорія ідеального газу

Основні формули

1. Рівняння стану ідеального газу або рівняння Клапейрона

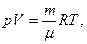
де p – тиск газу;

V – його об'єм;

T – абсолютнатемпература;

m – маса газу;

m – маса одного моля газу;

R =8,31 Дж/(моль^.К) – газова стала;

m/m – число молів.

2. Кількість речовини газу (у молях)

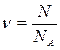або

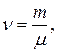
де N – число молекул газу;

N_A = 6,02^.10 ²³ моль^-1 – постійна Авогадро.

3. Кількість речовини в суміші газів визначається

n = n₁+n₂+...+n_n = N₁/N_A + N₂/N_A + ... + N_n/N_A

або

n = m₁/m₁ + m₂/m₂ + ... + m_n/m_n ,

де n_i, N_i, m_i, m_i – відповідно кількість речовини, число молекул, маса, молярна маса i-ї компоненти суміші.

4. Молярна маса суміші газів

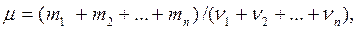
де m_i – маса i-ї компоненти суміші;

n_i – кількість речовини i-ї компоненти суміші;

n – число компонент суміші.

Масова частка w_i i-ї компоненти суміші газів (у долях одиниці)

,

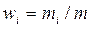де m – маса суміші.

5. Концентрація молекул

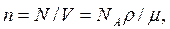
де N – число молекул, що втримуються в даній системі;

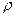– густина речовин;

V – об'єм системи.

Формула справедлива не тільки для газів, але й для будь-якого агрегатного стану речовини.

6. Тиск суміші газів (закон Дальтона) дорівнює сумі їх парціальних тисків

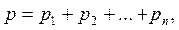
де n – число компонент суміші.

Парціальним тиском називається тиск газу, який мав би кожен газ, що входить до складу суміші, за умови, що при даній температурі він один заповнював би весь об'єм.

7. Основне рівняння молекулярно-кінетичної теорії газів

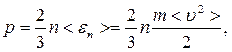
де n – число молекул в одиниці об'єму;

<e_n> – середня енергія поступального руху однієї молекули;

m – маса молекули;

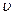< ²> – середнє значення квадрата швидкості.

8. Середня кінетична енергія поступального руху молекули

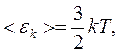
де k = R/N_a = 1,38 ^. 10^-23 Дж/К – стала Больцмана.

9. Середня повна кінетична енергія молекули

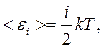
де i – число ступенів вільності молекули.

Для одноатомного газу i = 3; для двохатомного газу i = 5; для багатоатомного газу i = 6.

10. Залежність тиску газу від концентрації молекул і температури

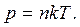
11. Швидкості газових молекул:

- середня квадратична швидкість

;

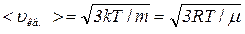- середня арифметична швидкість

;

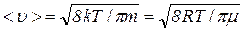- найбільш імовірна швидкість

,

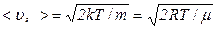де m – маса однієї молекули.

12. Відносна швидкість молекули

,

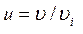де 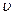– швидкість даної молекули;

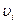– найбільш імовірна швидкість.

13. Закон розподілу молекул за швидкостями (закон Максвелла) дозволяє знайти число молекул dN, відносні швидкості яких лежать в інтервалі від u до u+ du,

.

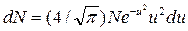де du – величина інтервалу відносних швидкостей мала в порівнянні зі швидкістю u;

N – загальне число молекул в системі.

Щоб визначити, яка частина молекул DN/N має відносні швидкості в діапазоні від u₁ до u₂, треба розрахувати такий вираз

.

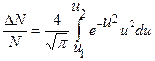14. Класичний розподіл Максвелла буде мати інший вигляд, якщо відносну швидкість виразити через значення середньої і найбільш імовірної швидкостей

,

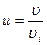звідки

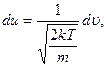а також 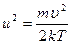і .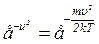

Після підстановки цих значень у формулу розподілу Максвелла через відносні швидкості одержуємо цей же розподіл в іншому вигляді

.

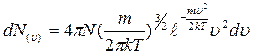15. Розподіл Больцмана (розподіл частинок у силовому потенціальному полі U_n

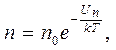
де n – концентрація частинок в тих точках силового поля, де потенціальна енергія U_n;

n₀ – концентрація частинок у тих точках силового поля, де W_n=0.

16. Середня довжина < l > вільного пробігу молекул газу

,

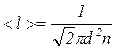де d – ефективний діаметр молекул;

n – концентрація молекул газу.

17. Середнє число зіткнень молекул за одиницю часу

=

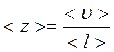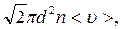
де 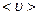– середня швидкість газових молекул;

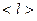– довжина вільного пробігу молекул;

d – ефективний діаметр молекули;

n – концентрація молекул газу.

18. Динамічна в’язкість газового середовища

η = ,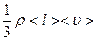

де ρ – густина газу (рідини);

< l > – середня довжина вільного пробігу молекул.

19. Закон Ньютона

F =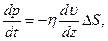

де η – коефіцієнт динамічної в’язкості;

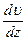– градієнт швидкості газу;

ΔS – площадка переносу газу.

20. Закон Фурє

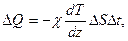
де χ = 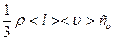– коефіцієнт теплопровідності газу;

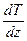– градієнт температури;

ΔS – площадка переносу газу;

Δt – час переносу теплової енергії;

с_υ – теплоємність газу при сталому об’ємі.

21. Закон Фіка

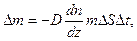
де – D = 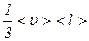– коефіцієнт дифузії газу;

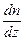– градієнт концентрації газу;

m – маса однієї молекули газу.