Привести примеры векторных величин, известных из физики.

Как от точки отложить вектор, равный данному.

(Векторы называются равными, если они сонаправлены и их длины равны.)

если быть досконально точным: приложить к данному вектору линейку, измерить длину вектора и ,не изменяя угла под которым лежит линейка относительно края тетради переместить её по тетради так, чтобы начальная точка делений на линейке (0) совпадала с данной нам точкой и провести вектор, длину которого мы уже измерили .

4. Вычитание векторов.

Разностью векторов a и b называется такой вектор, сумма которого с вектором b равна вектору a.

Для этих векторов (a и b ) справедливо равенство a - b = а + ( -b) .

5. Определение и теорема средней линии трапеции.

Определение: средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции.

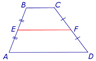
Теорема: Средняя линия трапеции параллельна ее основаниям и равна их полусумме.

6. Определение равных векторов.

Векторы называются равными, если они сонаправлены и их длины равны.

7. Определение нулевого вектора.

Нулевой вектор — вектор, начало которого совпадает с его концом.

8. Определение сонаправленных векторов.

Два коллинеарных вектора называются сонаправленными векторами, если их направления совпадают. (+ все нулевые векторы сонаправлены.)

9. Умножение вектора на число.

Произведением ненулевого вектора a на число k называется такой вектор b, длина которого равна | k | ⋅ | a |, при чём векторы a и b сонаправлены при k ⩾ 0 и противоположно направлены при k < 0.

Привести примеры векторных величин, известных из физики.

Скорость, сила, ускорение, перемещение…

11. Что называется длиной вектора?

Длиной или модулем ненулевого вектора 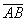называется длина отрезка 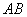. Длина нулевого вектора равна нулю.

12. Определение противоположно направленных векторов.

Два коллинеарных вектора называются противоположно направленными векторами, если они направлены в разные стороны.

13. Правило многоугольника (сумма нескольких векторов).

От произвольной точки А плоскости или пространства откладывается вектор, равный первому слагаемому, от его конца откладывается вектор, равный второму слагаемому, от его конца откладывается третье слагаемое, и так далее. Пусть точка В - это конец последнего отложенного вектора. Суммой всех этих векторов будет вектор АВ.

Сложение нескольких векторов на плоскости таким способом называется правилом многоугольника.

(+ сумма нескольких векторов не зависит от того, в каком порядке они складываются.)

14. Свойства умножения вектора на число. Произведение векторов.

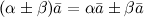
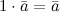
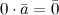
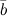(Здесь и - произвольные векторы, 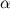, 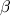- произвольные числа.)

15. Определение и теорема средней линии треугольника.

Определение: Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника.

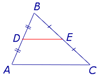
Теорема: Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.

16. Сложение векторов с помощью правила треугольника.

Сложение векторов и 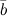осуществляется по правилу треугольника:

Суммой 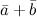двух векторов и 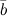называют такой третий вектор , начало которого совпадает с началом , а конец - с концом .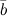

17. Сложение векторов с помощью правила параллелограмма.

Правило параллелограмма - если два неколлинеарных вектора и 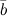привести к общему началу, то вектор 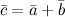совпадает с диагональю параллелограмма, построенного на векторах и 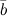. Причем начало вектора совпадает с началом заданных векторов.

18. Сложение векторов. Законы сложения векторов.

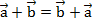– пе­ре­ме­сти­тель­ный закон

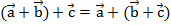– со­че­та­тель­ный закон

19. Чему равна длина вектора?

Его модулю.