Явление электромагнитной индукции. ЭДС индукции. Закон Фарадея. Правило Ленца. Самоиндукция. Индуктивность соленоида. Включение и отключение катушки от источника постоянной ЭДС.

Действие магнитного поля на проводник с током. Сила Ампера. Взаимодействие параллельных токов.

Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение зарядов в магнитных полях.

Циркуляция вектора индукции магнитного поля. Вихревой характер магнитного поля. Закон полного тока. Магнитное поле соленоида.

Магнитный поток. Работа перемещения проводника и контура с током в магнитном поле.

Тема 2.

Явление электромагнитной индукции. ЭДС индукции. Закон Фарадея. Правило Ленца. Самоиндукция. Индуктивность соленоида. Включение и отключение катушки от источника постоянной ЭДС.

При изменении потока магнитной индукции через поверхность замкнутого проводящего контура в контуре возникает электрический ток. Это явление называют электромагнитной индукцией, а возникающий ток индукционным.

ЭДС индукции– возникает в контуре при изменении магнитного потока.

При изменениях магнитного потока в контуре возникает электродвижущая сила индукции .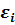

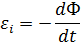
Закон Фарадея: какова бы ни была причина изменения потока магнитной индукции через поверхность замкнутого проводящего контура, возникающая в контуре э.д.с. индукции равна скорости изменения магнитного потока со знаком «минус».

Пусть контур, в котором индуцируется э.д.с., состоит не из одного витка, а из N витков, например, представляет собой соленоид – провод, навитый на круглый цилиндрический каркас. Поскольку витки соединяются последовательно, 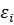будет равна сумме э.д.с., индуцируемых в каждом из витков в отдельности:

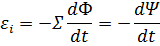
Величину 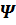называют потокосцеплением или полным магнитным потоком.

Если поток, пронизывающий каждый из витков, одинаков,

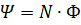
Э.д.с., индуцируемая в сложном контуре, равна:

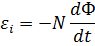
Правило Ленца: индукционный ток имеет всегда такое направление, чтобы препятствовать причине, его вызывающей.

Рассмотрим следующий пример:

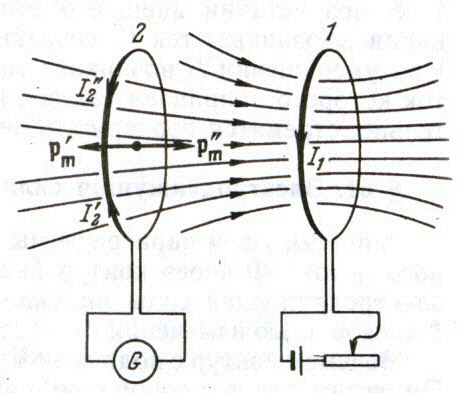
На рис. изображён контур 1, силу тока в котором 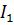можно изменять с помощью реостата. Этот ток создаёт магнитное поле, пронизывающее контур 2. Если увеличивать ток 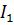, поток магнитной индукции Ф через контур 2 будет расти. Это приведёт к появлению в контуре 2 индукционного тока 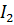, регулируемого гальванометром. Уменьшение тока 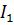обусловит убывание магнитного потока через второй контур, что приведёт к появлению в нём индукционного тока иного направления. Индукционный ток 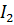можно вызвать также, приближая контур 2 к контуру 1 или удаляя второй контур от первого. В обоих случаях направления возникающего тока противоположны.

Пусть оба контура неподвижны. При увеличении тока 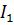, т.е. возрастании внешнего магнитного потока, направленного вправо, возникает ток 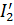, создающий поток, направленный влево. При уменьшении 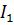возникает ток 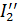, собственный магнитный поток которого направлен также, как и внешний поток, и, следовательно, стремится поддержать внешний поток неизменным.

Самоиндукция.

При изменении силы тока в замкнутом проводящем контуре изменяется магнитный поток, вследствие чего в контуре индуцируется э.д.с. Это явление называется самоиндукцией.

В соответствии с законом Био-Савара магнитная индукция B пропорциональна силе тока: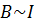

Следовательно, ток I в контуре и создаваемый им полный магнитный поток Ψ через контур пропорциональны друг другу:

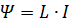
Коэффициент пропорциональности Lмежду силой тока и полным магнитным потоком называется индуктивностью контура.

При изменениях силы тока в контуре возникает э.д.с. самоиндукции, равная:

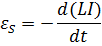
Если при изменениях силы тока индуктивность остаётся постоянной (возможно при отсутствии ферромагнетиков):

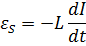
Индуктивность соленоида.

При протекании тока I по соленоиду внутри соленоида возбуждается однородное поле, индукция которого равна:

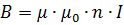
Поток через каждый из витков равен:

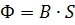
Полный магнитный поток, сцеплённый с соленоидом:

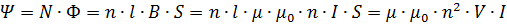
где l – длина соленоида,

n – число витков на единицу длины,

S – площадь поперечного сечения,

V – объём соленоида,

μ - магнитная проницаемость среды;

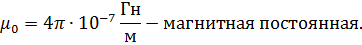
Индуктивность соленоида равна: