Мета роботи. Вивчити вільні затухаючі коливання пружинного маятника, визначити параметри коливальної системи та характеристики коливань (жорсткість пружини

Вивчити вільні затухаючі коливання пружинного маятника, визначити параметри коливальної системи та характеристики коливань (жорсткість пружини, коефіцієнт опору, період коливань, логарифмічний декремент, коефіцієнт затухання), а також дослідити їх залежність від маси маятника.

2. Теоретичні відомості.

Пружинним маятником називають систему, яка складається з невеликого тіла масою m, підвішеного на вертикальній пружині жорсткістю k, другий кінець якої закріплений. Масою пружини нехтують (рис. 1).

В положенні рівноваги (x =0) сила тяжіння, що діє на кульку врівноважується силою пружності:

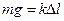, (1)

де 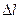- видовження пружини в стані рівноваги.

Рис. 1.

При зміщенні тіла від положення рівноваги сила пружності буде більшою або меншою за силу тяжіння і їхня рівнодійна F буде направлена до положення рівноваги, а її модуль дорівнюватиме:

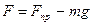(2)

За законом Гука:

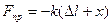, (3)

де x – зміщення системи від положення рівноваги, 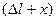- величина деформації пружини, знак “-” свідчить про те, що сила пружності за напрямком протилежна до деформації.

Підставимо у формулу (2) вирази (3) та (1) і отримаємо:

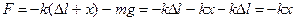(4)

Рівнодійна сил пружності і тяжіння пропорційна зміщенню x і направлена до положення рівноваги, тобто є повертаючою силою, під дією якої в системі відбуваються вільні коливання.

Крім повертаючої сили F на систему діє сила опору середовища, в якому вона перебуває.

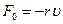, (5)

де r – коефіцієнт опору, 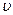– швидкість системи. Знак “-” свідчить про те, що сила опору направлена проти швидкості.

Запишемо закон динаміки для руху тіла:

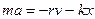(6)

Підставимо в це рівняння вираз для швидкості та прискорення та отримаємо:

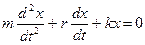
Поділимо рівняння на m і введемо позначення:

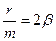(7)

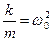, (8)

де r, m, k – параметри пружинного маятника.

Тоді остаточно диференціальне рівняння затухаючих коливань матиме вигляд:

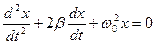. (9)

Розв’язком цього рівняння є функція:

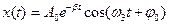. (10)

Вільні коливання пружинного маятника є затухаючими з амплітудою 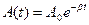,та частотою 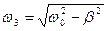; де 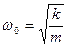- власна частота коливань пружинного маятника.

За формулою зв’язку між періодом та частотою отримаємо вираз для періоду коливань пружинного маятника:

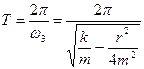. (11)

Логарифмічний декремент затухання, який характеризує зменшення амплітуди за період коливань, дорівнює:

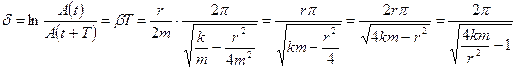. (12)

З рівнянь (7), (11), (12) видно, що коефіцієнт затухання, період, логарифмічний декремент затухання залежать від параметрів системи.

3. Методика вимірювання.

Методика виконання даної роботи полягає в тому, що за виміряним значенням амплітуди коливань А₀ в початковий момент часу та амплітуди А_n через час t, за який відбулось n коливань, визначається період коливань T, коефіцієнт затухання β та логарифмічний декремент затухання δ за формулами:

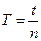, (13)

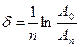, (14)

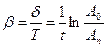, (15)

Для визначення жорсткості пружини використовується додатковий тягарець масою М, який додається до тіла, підвішеного на пружині, і призводить до її додаткового видовження .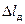

Тоді за умови рівноваги:

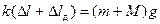
розкриємо дужки і отримаємо:

.

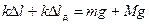Враховуючи вираз (1) остаточно отримаємо формулу для розрахунку жорсткості пружини:

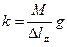. (16)

Коефіцієнт опору r згідно виразу (7):

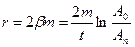. (17)