Описание лабораторного макета. Лабораторная работа выполняется на компьютере с использованием виртуального макета

Лабораторная работа выполняется на компьютере с использованием виртуального макета. Структурная схема макета приведена на рис. 2.

Двоичный источник сообщений генерирует последовательность знаков алфавита {A; B} длина сообщения N (N изменяется вручную). Источник может быть трех типов:

- без памяти с равными вероятностями знаков;

- без памяти с разными вероятностями знаков;

- марковский источник с памятью 1-го порядка.

Укрупнение алфавита можно осуществлять по 2, по 3 и по 4 знакам. Для укрупненного алфавита используется алгоритм Хаффмана.

Установка N

Рисунок 2 – Структурная схема лабораторного макета

Требования к отчету

7.1 Название лабораторной работы.

7.2 Цель работы.

7.3 Результаты выполнения домашнего задания.

7.4 Структурные схемы исследований и результаты выполнения пп. 5.2...5.4 лабораторного задания (таблицы, расчеты).

7.5 Выводыпо каждому из пунктов задания, в которых представить анализ полученных результатов.

7.6 Дата, подпись студента, виза преподавателя с оценкой в 100-балльной системе.

ЛР 2.3 Исследование алгоритма сжатия
дискретных сообщений LZW

Цель работы

1.1 Изучение алгоритма сжатия дискретных сообщений LZW.

1.2 Исследование зависимости коэффициенту сжатия от свойств сообщения и параметров кодера LZW.

Ключевые положения

2.1 Дискретным сообщением является такое, которое состоит из символов конечного алфавита 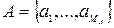, например, текстовое сообщение. Для передачи дискретных сообщений каналами связи каждому символу сообщения a_i ставится в соответствие двоичная комбинация b_i, состоящая из n разрядов:

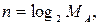(1)

где M_А – объем алфавита или количество знаков алфавита A; здесь и дальше считаем, число M_А есть целая степень числа 2.

Преобразования 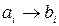называется примитивным или равномерным кодированиям. Примерами примитивных кодов являются международный телеграфный код МТК-2, американский стандартный код ASCII и прочие. Наиболее часто такое кодирование является избыточным, т.е. знаки сообщения можно передавать экономнее, комбинациями меньшей длины, чем n.

По теореме Шеннона для канала без помех можно закодировать сообщение так, что средняя длина кодовой комбинации 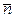будет сколь угодно близкой к энтропии источника сообщений:

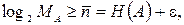(2)

где: H(A) – энтропия источника сообщений, дв.ед.;

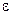– сколь угодно малая величина.

Такое кодирование называют эффективным кодированием или сжатием сообщения без потерь информации.

Из выражения (2) вытекает, что сжатие сообщения без потерь информации будет иметь место, лишь когда 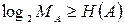. Таким образом, значение 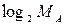является максимальным значением энтропии источника сообщений и достигается оно, когда символы сообщения статистически независимые и равновероятные. Однако в большинстве случаев сообщения имеют избыточность, т.е. символы сообщения статистически зависимы и имеют разные вероятности, например, как в текстовых сообщениях.

2.2 Для того, чтобы сжать сообщение, кодер (алгоритм сжатия) должен устранить причины избыточности сообщения. Алгоритмы сжатия делятся на три класса:

- алгоритмы, которые устраняют разновероятность символов;

- алгоритмы, которые устраняют статистическую зависимость символов;

- универсальные алгоритмы, которые устраняют как разновероятность, так и статистическую зависимость символов.

К алгоритмам первого класса относятся классические коды Хаффмана и Шеннона-Фано. Алгоритмами второго класса являются словарными, наиболее распространенными из них алгоритмы Лемпеля-Зива: LZ77, LZ78, LZW и их модификации. Универсальными алгоритмами, позволяющие как угодно приблизить среднюю длину комбинации к энтропии источника, т.е. 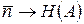, являются арифметические коды.

Наибольшее распространение алгоритмы сжатия без потерь информации получили в компьютерных программах-архиваторах: RAR, ZIP и других. Все современные архиваторы являются комбинированными, т.е. строятся на основе двух алгоритмов. Первым алгоритмом всех архиваторов является LZ77 или его модификации. Вторым алгоритмом является адаптивный код Хаффмана. В итоге устраняются обе причины избыточности.

Наиболее известным примером использования алгоритмов сжатия без потерь информации в системах связи является протокол V.42bis, который используется в модемах V.42 для передачи по телефонным каналам. Ядром этого протокола является алгоритм сжатия LZW – модификация классического алгоритма LZ78, предложенная Т. Уелчем. Итак, в модемах V.42 устраняется лишь статистическая зависимость между символами, поскольку адаптивный код Хаффмана, устраняющий разновероятность символов, является неэффективным с точки зрения быстродействия, поскольку данные должны передаваться модемом без значительной задержки.

2.3 Особого внимания заслуживают словарные алгоритмы сжатия LZ77, LZ78 и LZW. Безоговорочным преимуществом этих алгоритмов является их адаптивность, т.е., эти алгоритмы одинаково сжимают сообщения разных алфавитов, например, текстовые сообщения разных языков. Арифметический код и код Хаффмана (которые довольно простые) предназначены для сжатия, например, английских текстов не смогут эффективно сжать, например, украинский текст. Для того чтобы арифметический код или код Хаффмана одинаково эффективно сжимали сообщения разных алфавитов, они должны быть адаптивными, что значительно усложняет эти алгоритмы и уменьшает их быстродействие.

2.4 Наиболее совершенным словарным алгоритмом сжатия считается LZW. Принцип работы алгоритма LZW можно изложить тремя пунктами:

- в процессе кодирования сообщение разбивается на последовательности знаков, которые не повторяются – на строки;

- строки нумеруются – формируется словарь;

- по каналу передается номер строки, по которому можно восстановить соответствующую строку.

Для того чтобы алгоритм был однозначным, словарь необходимо инициализировать, т.е. сформировать его начальные значения. Для инициализации словаря выбирают любой примитивный код, например, ASCII. Этот код восьмиразрядный, 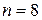, и позволяет закодировать 256 знаков, которые являются элементарными строками. Процедура инициализации словаря состоит в том, что этим знакам приписываются номера от 0 до 255. В результате к началу сжатия словарь имеет вид табл. 1.

Таблица 1 – Инициализированный словарь

Строка	Номер строки в десятичной системе исчисления	Номер строки в двоичной системе исчисления
"NULL"		00 0000 0000
...	...	...
"А"		00 0100 0001
"В"		00 0100 0010
"С"		00 0100 0011
"D"		00 0100 0100
...	...	...
"ٱ"		00 1111 1111
...	...	...

Из табл. 1 видно, что номера строк десятиразрядные, а не восьмиразрядные. Это необходимо для того, чтобы в процессе сжатия можно было расширять словарь, т.е. дополнять его новыми строками. Всего в приведенный в табл. 1 словарь может быть записано 1024 строк. Итак, объем словаря определяется:

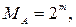(3)

где 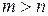– количество разрядов для представления номера строки.

После инициализации словаря начинается процесс сжатия:

1) во входной буфер заносятся символы до тех пор, пока не окажется, что строка, образуемая этими символами, уже есть в словаре;

2) если при занесении во входной буфер следующего символа образуется отсутствующая в словаре строка, то такая строка заносятся в словарю, как новая;

3) на выход кодера (в канал связи) подается номер последней найденной в словаре строки, а в буфере остается последний из занесенных символов.

Работа алгоритма представлена в табл. 2 на примере сообщения: "ABABCABCABCA".

Кодер выполняет шагами 1…12 следующие действия:

1. Входной символ A, во входной буфер заносим символ "A", который есть в словаре. В словарь ничего не записывается, ничего не передается. Во входной буфер заносим "A".

2. Входной символ B, во входной буфер заносим символ "AB", которого нет в словаре. В словарь записывается строка "AB" под номером 256, передается содержимое предыдущего состояния входного буфера, т.е. код буквы "A" – 65. Во входной буфер заносим "B".

3. Входной символ А, во входной буфер заносим символ "ВА", которого нет в словаре. В словарь записывается строка "ВА" под номером 257, передается содержимое предыдущего состояния входного буфера, т.е. код буквы "B" – 66. Во входной буфер заносим "A".

4. Входной символ В, во входной буфер заносим символ "AB", который есть в словаре. В словарь ничего не записывается, ничего не передается. Во входной буфер заносим "AB".

5. Входной символ C, во входной буфер заносим символ "ABC", которого нет в словаре. В словарь записывается строка "ABC" под номером 258, передается содержимое предыдущего состояния входного буфера, т.е. код буквы "AB" – 256. Во входной буфер заносим "С".

Таблица 2 – Пример сжатия сообщения за алгоритмом LZW

№	Символ	Входной буфер	Есть в словаре?	Занести в словарь	Передается	Входной буфер
строка	под номером
	A	"A"	да	-	-	-	"A"
	B	"AB"	нет	"AB"			"B"
	А	"ВА"	нет	"ВА"			"A"
	B	"AB"	да	-	-	-	"AB"
	C	"ABC"	нет	"ABC"			"C"
	A	"CA"	нет	"CA"			"A"
	B	"AB"	да	-	-	-	"AB"
	C	"ABC"	да	-	-	-	"ABC"
	A	"ABCA"	нет	"ABCA"			"A"
	B	"AB"	да	-	-	-	"AB"
	C	"ABC"	да	-	-	-	"ABC"
	A	"ABCA"	да	-	-		""

6. Входной символ А, во входной буфер заносим символ "CA", которого нет в словаре. В словарь записывается строка "CA" под номером 259, передается содержимое предыдущего состояния входного буфера, т.е. код буквы "С" – 67. Во входной буфер заносим "А".

7. Входной символ В, во входной буфер заносим символ "AВ", который есть в словаре. В словарь ничего не записывается, ничего не передается. Во входной буфер заносим "AВ".

8. Входной символ С, во входной буфер заносим символ "AВС", который есть в словаре. В словарь ничего не записывается, ничего не передается. Во входной буфер заносим "AВС".

9. Входной символ А, во входной буфер заносим символ "АВCA", которого нет в словаре. В словарь записывается строка "АВCA" под номером 260, передается содержимое предыдущего состояния входного буфера, т.е. код буквы "АВС" – 258. Во входной буфер заносим "А".

10. Входной символ В, во входной буфер заносим символ "AВ", который есть в словаре. В словарь ничего не записывается, ничего не передается. Во входной буфер заносим "AВ".

11. Входной символ С, во входной буфер заносим символ "AВС", который есть в словаре. В словарь ничего не записывается, ничего не передается. Во входной буфер заносим "AВС".

12. Входной символ А, во входной буфер заносим символ "AВСА", который есть в словаре. В словарь ничего не записывается. Так как на входе кодера символов больше нет, передается содержимое входного буфера, т.е. "AВСА" – 260.

Итак, в результате сжатия сообщения "ABABCABCABCA" каналом связи передается последовательность из шести чисел: 65 66 256 67 258 260.

2.5 Все алгоритмы сжатия, в том числе и алгоритм LZW, характеризуются тремя параметрами:

- коэффициентом сжатия h;

- скоростью сжатия и декодирования сообщения;

- объемом памяти, необходимой для работы кодера и декодера.

Скорость сжатия, декодирование и объем памяти на сегодня уже не являются определяющими при выборе того или другого алгоритма сжатия – определяющим параметром является коэффициент сжатия, который обеспечивается заданным алгоритмом сжатия.

Коэффициентом сжатия называется отношение:

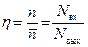, (4)

где: N_вх – количество двоичных символов, используемых для представления сообщения на входе кодера;

N_вых – количество двоичных символов, используемых для представления сообщения на выходе кодера.

2.6 Количество двоичных символов на входе кодера, необходимых для представления сообщения "ABABCABCABCA", равняется произведению количества символов сообщения и количества разрядов: 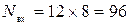. Соответственно, количество двоичных символов на выходе кодера: 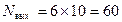. Таким образом, сообщение "ABABCABCABCA" сжато в 1,6 раза.

Пусть теперь сообщение состоит лишь из трех символов "ABA". В этом случае на выходе кодера будет наблюдаться следующая последовательность чисел: 65 66 65. В результате, коэффициент сжатия меньше единицы: 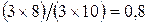. Таким образом, кодер не сжимает сообщения, а наоборот, увеличивает избыточность.

Последний пример показывает основной недостаток всех словарных алгоритмов – плохое сжатие коротких сообщений. Этот факт объясняется тем, что в процессе сжатия таких сообщений словарь практически не заполняется, и, в основном, кодируются одиночные символы, а не последовательности символов.

2.7 В значительной мере определяющим моментом процесса сжатия сообщения по алгоритму LZW является момент полного заполнения словаря. В классическом алгоритме LZW, который изучается, после заполнения словарь не изменяется, а на выходе кодера появляются номера строк, присутствующие в этом словаре.

Процесс заполнения словаря – это процесс описанной адаптации алгоритма к кодируемому сообщению, и пока заполняется словарь, постоянно возрастает коэффициент сжатия. Как только словарь заполнится, алгоритм перестает адаптироваться к сообщению, а коэффициент сжатия перестает увеличиваться.

Классическое решение этой проблемы в алгоритме LZ78 – сброс словаря после его полного заполнения. После сброса словаря процесс его заполнения повторяется. Таким образом алгоритм адаптируется к отдельным частям сообщения, позволяющий несколько увеличить коэффициент сжатия. Недостаток этого решения – малый коэффициент сжатия в начале заполнения словаря.

Также классическое решение проблемы – увеличение объема словаря. Теоретически неограниченный по объему словарь позволяет достичь максимально возможного коэффициента сжатия 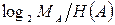, но при значительном увеличении M_А значительно возрастает время, необходимое на поиск строки в словаре, т.е. уменьшается скорость сжатия. Так, протокол V.42bis не ограничивает объем словаря, указывается лишь минимально возможное значение – .

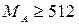Наиболее удачное решение – не прекращать заполнение словаря. В этом случае номера строк в словаре постоянно изменяются. Номера строк, которые встречаются очень часто, уменьшаются, т.е. эти строки располагаются в начале словаря. Строки, которые встречаются редко, располагаются в конце словаря. Когда словарь заполнен, то новая строка заносится в словарь вместо последней строки, которая реже всего встречается в сообщении.

2.8 Поиск строк в словаре является отдельной задачей, а его эффективность определяет скорость сжатия. Важно, что при увеличении объема словаря для увеличения коэффициента сжатия, уменьшается скорость поиска строк в словаре. Чтобы увеличить скорость сжатия, одновременно с увеличением объема словаря ограничивается длина строки в словаре N_C. Т.е., в словарь не заносятся строки, длина которых превышает N_C, но при этом, снова таки, несколько уменьшается коэффициент сжатия. В протоколе V.42bis указывается, что максимальная длина строки может изменяться в диапазоне от 6 до 250 символов.

2.9 Преимуществом алгоритма LZW является то, что декодирование сообщения не нуждается в дополнительных данных и осуществляется с высокой скоростью. Принцип декодирования аналогичный сжатию:

1) словарь декодера инициализируется таким же образом, как и словарь кодера;

2) за принятым номером в словаре отыскивается соответствующая строка;

3) найденная строка подается на выход декодера;

4) в словарь заносится строка, которая состоит из предыдущей строки и первого символа текущей строки.

Пример декодирования сжатого по алгоритму LZW сообщения "65 66 256 67 258 260" приведено в табл. 3. Необходимо обратить внимание на исключительную ситуацию, когда принимается номер строки, которой еще нет в словаре. В этом случае строка заносится в словарь в процессе декодирования: первая строка состоит из предыдущей строки и ее первого символа.

Таблица 3 – Пример декодирования сообщения за алгоритмом LZW

Номер	Есть в словаре?	Декодированная строка	Буфер	Занести в словарь	Буфер
строка	под номером
	да	"А"	"А"	-	-	"А"
	да	"В"	"АВ"	"АВ"		"В"
	да	"АВ"	"ВА"	"ВА"		"АВ"
	да	"С"	"АВС"	"АВС"		"С"
	да	"АВС"	"СА"	"СА"		"АВС"
	нет	"АВСА"	"АВСА"	"АВСА"		"АВСА"

2.10 Известный факт, что сообщения с малой избыточностью очень чувствительны к ошибкам, возникающим в каналах связи. Например, если при передаче первого числа сжатого сообщения состоится ошибка и будет принято число "193" вместо "65", то наступит коллизия, которую декодер не способен решить. В таком случае, согласно протоколу V.42bis, осуществляется запрос на повторную передачу. Но более опасными являются ошибки, которые не приводят к коллизиям. Например, ошибка происходит в четвертом числе и принимается последовательность "65 66 256 66 258 260". На выходе декодера получим "АВАВВАВВАВВА". Таким образом, одна ошибка привела к появлению еще двух, т.е. наблюдается явление размножения ошибок. Итак, в случае сжатия сообщений к каналам связи предъявляются жесткие требования.

Ключевые вопросы

3.1 Что называется примитивным кодированием?

3.2 Что называется эффективным кодированием или сжатием сообщения?

3.3 Назвать причины избыточности сообщений.

3.4 Дать определение коэффициенту сжатия?

3.5 Чему равен максимальный коэффициент сжатия в случае сжатия без потерь информации?

3.6 Назвать известные алгоритмы сжатия сообщений без потерь информации.

3.7 Описать процесс сжатия сообщения по алгоритму LZW.

3.8 Описать процесс декодирования сообщения по алгоритму LZW.

Домашнее задание

4.1 Изучить по конспекту лекций и ключевым положениям раздел "Эффективное кодирование дискретных сообщений". При изучения раздела можно воспользоваться литературой [2, с. 16...27; 5, с. 876...887].

4.2 По алгоритму LZW выполнить сжатие сообщения, которое задано в табл. 4. Процесс сжатия оформить в виде табл. 2.

4.3 Декодировать сжатое в п. 4.2 сообщение. Процесс декодирования оформить в виде табл. 3.

4.4 Подготовиться к беседе по ключевым вопросам.

Таблица 4 – Исходные данные к домашнему заданию

Номер бригады	Сообщение
	AAABCD
	DAAABC
	CDAAAB
	BCDAAA
	ABCDAA
	AABCDA

Лабораторное задание

5.1 Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 2.3 Исследование алгоритма сжатия дискретных сообщений LZW, используя иконку Лабораторные работы на рабочем столе, а затем папки ТЭС и Модуль 2. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.2 Проверить правильность выполнения домашнего задания. Выбрать закладку “Сжатие сообщения”. Инициализировать словарь путем нажатия на кнопку "Инициализация словаря". После этого, в поле "Входные символы" ввести сообщение из домашнего задания. Для завершения введения сообщения необходимо нажать на кнопку "Завершить введение символов". Сжатие сообщения осуществляется в пошаговом режиме путем нажатия на кнопку "Начать сжатие". Каждое действие кодера объясняется в поле "Описание действия кодера". После завершения сжатия сообщения эта кнопка станет недоступной. Проверить правильность выполнения п. 4.2 домашнего задания. На любом шаге можно прекратить сжатие путем нажатия на кнопку "Очищение".

После того, как сообщение сжато, выбрать закладку "Декодирование сообщения". Осуществить инициализацию словаря, для чего нажать на кнопку "Инициализация словаря". Декодирование осуществляется в пошаговом режиме путем нажатия на кнопку "Начать декодирование". После завершения декодирования сообщения эта кнопка станет недоступной. Убедиться, что декодированное сообщение совпадает с заданным. На любом шаге можно прекратить декодирование путем нажатия на кнопку "Очищение".

5.3 Исследовать процесс сжатия и декодирования сообщения.Выполнить сжатие и декодирование сообщения, которое состоит из вашей фамилии и инициалов. Процесс сжатия оформить в виде табл. 2, а процесс декодирования – в виде табл. 3. Выполнить сжатие и декодирование сообщения "aaaaaaaaaaaaaaaaaaaaaaaaaaaa". Зафиксировать в протоколе процессы сжатия и декодирования в виде табл. 2 и табл. 3 соответственно. Обратить внимание на ситуацию, когда длина строки становится равной максимальной длине строки N_C.

5.4 Исследовать зависимость коэффициента сжатия от типа сообщения.Выбрать закладку "Коэффициент сжатия" и тип сообщения "Равновероятные и независимые символы". Установить значения: длины сообщения N = 1000 символов; объема словаря М_А = 512 строк; максимальной длины строки N_C = 6 символов. Нажать на кнопку "Пуск" и зафиксировать в протоколе значения коэффициента сжатия. Повторить измерение коэффициента сжатия, если тип сообщения "Типичный текст" и "Документ Word". Сделать выводы относительно полученных результатов.

5.5 Исследовать зависимость коэффициента сжатия от длины сообщения.Выбрать тип сообщения "Типичный текст". Установить значения: объема словаря М_А = 512 строк; максимальной длины строки N_C = 6 символов. Измерить значение коэффициента сжатия сообщения длинами N: 1, 5, 10, 25, 50, 100, 200. Результаты измерений представить в виде таблицы η(N). Сделать выводы.

5.6 Исследовать зависимость коэффициента сжатия от объема словаря.Выбрать тип сообщения "Типичный текст" и установить длину сообщения N = 5000 символов, максимальную длину строки в словаре N_C = 6. Измерить значение коэффициента сжатия для объемов словаря M_А: 512, 1024, 2048, 4096. Результаты измерений представить в виде таблицы η(М_А). Сделать выводы.

5.7 Исследовать зависимость коэффициента сжатия от максимальной длины строки в словаре.Установить максимальную длину строки N_C = 50 символов и повторить измерение п. 5.6. Результаты измерений представить в виде таблицы η(М_А). Сделать выводы.