Damped harmonic oscillation

The system looses energy by a drag force

F_D= – r×u,

or a voltage drope on the active resistor

u_R= R×i,

therefore the amplitude has exponential decay on time

A(t)=А₀×е^{- b×t}.

The equation of damped oscillations has a mode

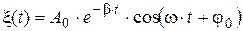, (3)

where x(t) – physical quantity, which oscillates; А₀ – initial amplitude of oscillations; b – damping coefficient; j₀ – initial phase (phase constant).

Cyclic frequency of damped oscillations (is written with no index) less then eigenfrequency:

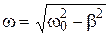. (4)

Parameters of linear damping oscillations:

1) Relaxation of vibrations – lessening of amplitude in е=2,71 times. The time of relaxation:

t = 1 / b. (5)

2) As far as amplitude of damped oscillations uninterruptedly decreases A(t)=А₀×е^-b×t , then the value of oscillating quantity x(t) will never repeat. That’s why, the quantity

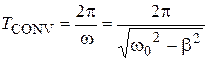(6)

is called conventional period – minimal time, during which the value of oscillating quantity x(t) will be equal peak magnitude (amplitude).

3) Decay decrement is a relation of two neibouring amplitude:

D = A_t / A_t+T = e ^{– b T} . (7)

4) Logarithmic decay decrement (damping constant):

d = lnD=bT_CONV , (8)

5) Quality factor of system

Q = w₀ / 2b . (9)

In equation of oscillations (2) it is described both mechanical, and electromagnetic oscillations, therefore it is possible to set up correspondence of mechanical and electrical oscillations’ parameters:

Mechanic oscillations	Electromagnetic oscillations
x(t)= x(t) – displacement from the equilibrium position of material point of oscillating device;	x(t)= q(t) – charge of oscillating circuit capacitor;
Parameters of a system:
k – spring constant (stiffness of spring). m – mass of oscillating device. r – drag coefficient.	С – electrocapacity of the capacitor. L – inductance of the inductance coil. R – resistance of circuit.
Damping coefficient:
;	;
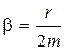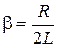Cyclic frequency of damped oscillations:
;	;
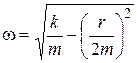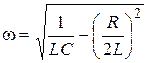Quality factor of system:
.	.

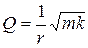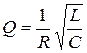EXAMPLE OF PROBLEM SOLUTION

Example 2. The oscillating RLC-circuit consists of capacitor, and coil of inductance of 2 mH and resistor. At the initial moment of time charge on the capacitor plates is maximal and equals q₀=Q₀=2mC. Conventional period of oscillations 1 ms, logarithmic decay decrement is 0,8.

1) To write down the equation of oscillations of charge with numerical coefficients.

2) To define the capacity of capacitor and the resistance of resistor.

Input data: L = 2 mH =0,002 H; Q0= 2 mC=2·10–6 C; ТCONV = 1s=10–3 s; δ= 0,8.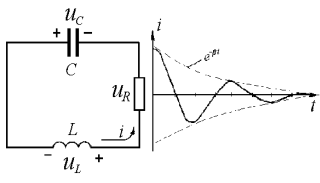
Find: q(t), С, R– ?

Solution:

1) Oscillations in circuit will be damping. Let’s write the equation of damped oscillations of charge in a general view:

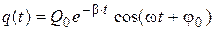, (2.1)

where Q₀ – the initial amplitude of charge, β – damping coefficient; ω – cyclic frequency of damped oscillations; j₀ – initial phase.

From a definition of the conventional period T_CONV=2p/w we express cyclic frequency of damped oscillations:

w =2p /T_CONV. (2.2)

From a definition of initial value of oscillating quantity q₀=Q×cos(j₀) and considering that the oscillations beginning from the position of maximal charge on the capacitor Q, we find the initial phase of oscillations:

j₀=arccos(q₀ /Q)= arccos(1)=0. (2.3)

From a definition of the logarithmic decay decrement is d=bT_CONV, whence the coefficient of damping

b=d /T_CONV. (2.4)

Let’s check, whether the right part of the formula (2.2) gives the unit of cyclic frequency [rad/s], and the left part of the formula (2.4) – measurement unit of damping coefficient [1/s]:

[w]= rad / s;

[b]= 1 / s.

Let’s substitute the numerical values in the formulas (2.2) and (2.4)

;

.

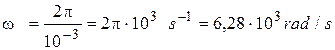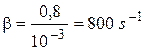Let’ write down the equation of oscillation of charge with numerical coefficients

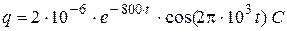. (2.5)

2) Let’s substitute the equation of eigenfrequency 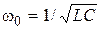into the definition of cyclic frequency of damped oscillations :

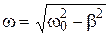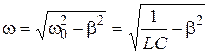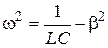Þ (2.6)

and find expression of capacity of capacitor:

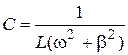. (2.7)

From a definition of the damping coefficient b=R/2L we obtain resistance of resistor R:

R = 2βL. (2.8)

Let’s check, whether the right part of the formula (2.7) gives the unit of electrocapacity [F], and the left part of formula (2.8) – the unit of resistance [Ω]:

;

.

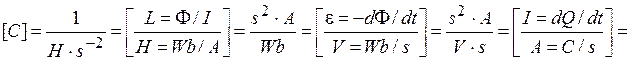
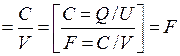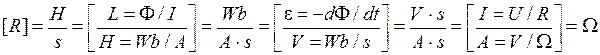Let’s make the calculations:

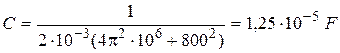; R = 2·300·2·10^-3= 3,2 W.

Results: 1) ,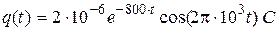

2) C=1,25×10^{-5 F}, R = 3,2 Ω.