Выбор шага квантования по времени

Известно несколько критериев выбора частоты квантования по времени. К таким критериям относится, в частности, частотный критерий В.А. Котельникова. Данный критерий, который получил название теоремы В.А. Котельникова, основывается на следующей модели сигналов:

- сигнал представляет собой стационарный случайный процесс;

- спектр сигнала сплошной и ограничен некоторой частотой, за пределами которой он тождественно равен нулю.

Теорема В.А. Котельникова: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число экстремумов) и ее спектр ограничен некоторой частотой f_c, то она полностью определяется отсчетами, находящимися на расстоянии 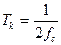друг от друга.

Для доказательства теоремы рассмотрим выражения прямого и обратного преобразования Фурье непрерывной функции x(t).

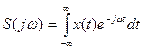, (1.62)

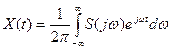. (1.63)

В рассматриваемом частном случае функции с ограниченным спектром можно записать

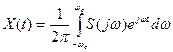. (1.64)

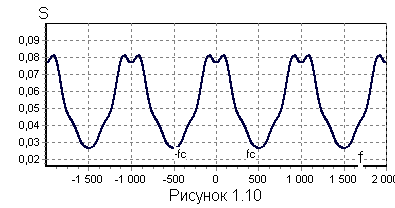
Дополним функцию до периодической с периодом, равным 2f_c (рисунок 1.10 ) и разложим ее в ряд Фурье.

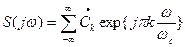, (1.65)

где . (1.66)

Сравнивая выражения (1.64) и (1.66) замечаем, что они совпадают с точностью до постоянного множителя 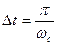, если принять .

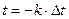Следовательно,

.

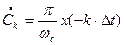Подставив найденное выражение для 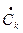в (1.65), получим

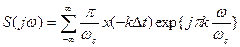. (1.67)

После подставки (1.67) в (1.64), замены знака при k (т.к. суммирование производится по всем положительным и отрицательным значениям k) и перестановки операций суммирования и интегрирования получим

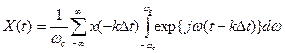. (1.68)

Вычислим интеграл

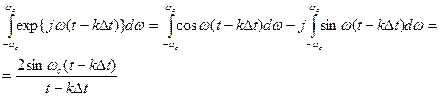(1.69)

т.к. .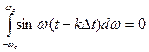

После подстановки (1.69) в (1.68) окончательно получим

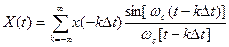. (1.70)

Полученное выражение представляет аналитически теорему
Котельникова.

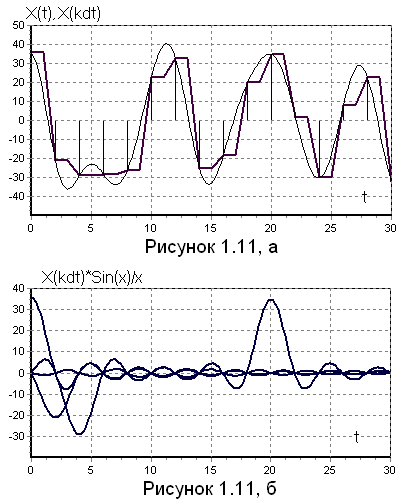
Из (1.70) видно, что непрерывная функция X(t) (рисунок 1.11, а), обладающая ограниченным спектром, может быть представлена разложением в ряд, каждый член которого выражается одинаковой функцией вида sin(x)/x (функция отсчета), но с различными коэффициентами 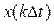(рисунок 1.11, б).

Ряд (1.70) представляет собой разложение случайного процесса с координатными функциями (детерминированными функциями времени) и весовыми коэффициентами 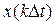, являющимися случайными величинами, равными мгновенным значениям сигнала в точках .

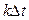Функция отсчетов в момент времени 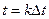достигает максимума и равна единице. В моменты времени 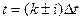, где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.

Сумма (1.70) в каждый k-ый момент времени определяется только одним k‑ым слагаемым, т.к. все остальные слагаемые в этот момент времени обращается в нуль. Внутри промежутка 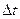восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).