Расчет гофров и поглощающих полостей

Несколько условно рассматривая ход так называемых критиче­ских, крайних лучей, можно методами геометрической оптики обозначить границы зон интенсивных отражений. Для иллюстра­ции основных идей геометрического расчета поверхности камеры в части формирования зон интенсивных отражений, рассмотрим вначале отражения от плоскости, на которой установлена рассеи­вающая конфигурация в виде продольного клина — гофра. Клин перекрывает своим основанием необходимое количество тпервых зон Френеля, вблизи точки стационарной фазы на плоскости.

Пусть размер основания клина b. Для выбора высоты клина h может быть использовано следующее соображение.

Пусть в плоскости расположения источника и точки наблюде­ния границы интенсивных полей, отраженных от граней клина и оставшейся части плоскости, находятся на одинаковом расстоянии от линии связи и границы безэховой зоны камеры (рис. 3.7). Если 1—1 — критический луч, отраженный от грани клина, а 2—2 — критический луч от оставшейся части плоскости, М — точка их пересечения на расстоянии H от отражающей плоскости, то, вво­дя c

tgc = h/b, (3.44)

получим 2b = (H - h)× tg2c (3.45)

Или, подставляя (3.44) в (3.45),

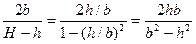(3.46)

или h = b²/H. (3.47)

До точки пересечения ближайшим к безэховой зоне является кри­тический луч 1—1, отраженный от грани клина, после точки пере­сечения — луч 2—2, отраженный от оставшейся части плоскости. Поле в безэховой зоне определяется «поперечной диффузией» этих лучей.

Однако изложенные выше соображения, приводящие к соотно­шению (3.47), для определения высоты гофра справедливы лишь тогда, когда один из размеров прямоугольного поперечного сече­ния камеры (в нашем случае H), существенно меньше второго размера и поле в безэховой зоне определяется, в основном, отра­жениями от близлежащей поверхности.

В более часто встречающемся случае, когда оба размера по­перечного сечения камеры примерно равны, для формирования зоны поглощения полей, отраженных в БЭК, необходимо рассмат­ривать переотражения в полостях, образованных двумя смежными частями замкнутой поверхности безэховой камеры.

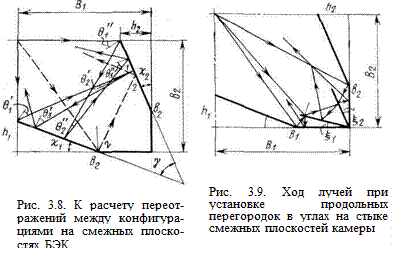
Рассмотрим один квадрант объема камеры (рис. 3.8). Углы при основании клиньев соответствуют определяемым по формуле

c₁ = arctg(h₁/b₁), c₂ = arctg(h₂/b₂) (3.48)

Для критического луча типа 1—1 углы падения на поверхность в квадранте

q¢₁ = c₁ и q² = c₂ . (3.49)

Как видно из рис. 3.8, при втором отражении в полости угол падения

q₁ = q₁ - g, g = p/2 - c₁ - c₂ (3.50)

При п-m переотражении угол падения

q₁ = q₁ - (n - 1)×g. (3.51)

Сформулировав условия выхода волны из поглощающей полости в виде

q_n ³ -q₁. (3.52)

С учетом (3.51) получим следующее соотношение для определения количества переотражений в поглощающей полости:

n £ 2q₁ / g + 1. (3.53)

Подставляя в (3.53) q₁ и gиз (3.49) и (3.50), получаем для критического луча, типа 1—1

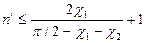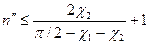, . (3.54)

Для

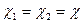
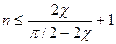. (3.55)

Соотношение (3.55) позволяет определить %, при котором обеспечивается за­данное п количество переотражений в полости, c ³ p×(n - 1) / 4n (3.56)

n
c		22,5°	30°	33,7°

На основании (3.56)

Если bп<В_п, т. е. конфигурация не перекрывает всю плоскость, необходимо рассмотреть еще переотражения в квадрате лучей типа 2—2 (рис. 3.8). Для них угол падения на полость

q¢₁ = arctg(b₁/B₂), q²₁ = arctg(b₂/B₂), (3.57)

а угол при вершине полости g^{I (II)} = p/2 -c₂₍₁₎. (3.58)

Соотношение (3.53) с учетом (3.57) и (3.58) дает

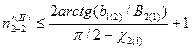. (3.59)

Для случая b₁/B₂ = b₂/B₁ = b/B и c₁ = c₂ = c

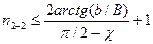. (3.59¢)

Взяв c = 33,7° (соответствует n_1-1 = 4 для луча типа 1-1), для b₁/B₂ = 0,5 и b₂/B₁= 0,75 убеждаемся, что при n¢_2-2 £ l,94, n²_2-2 £ 2,309 для луча, идущего к основанию конфигураций, образуется не более двух переотражений в полости.

Для увеличения количества переотражений этих лучей без уве­личения поперечных размеров камеры предложено в углах БЭК установить продольные перегородки, как показано на рис. 3.9.

Угол наклона x перегородки к защищаемой плоскости опреде­ляется из (3.53), положив g=x, и определив для луча типа 2—2 q_i из выражения (3.57). Итак, n_пер £ 2q₁/x+1. При x = q₁ n_пер=3. Для n = 4и x £ 2q₁/3 имеем

b/B	q1	x
0,5 0,75	26,56° 36,87°	17, 7° 24,58°

Легко убедиться, что, установив два поглощающих экрана под углами 24,6° к каждой из смежных ортогональных плоскостей по­верхности БЭК, мы получим всюду кратность переотражения геометрооптического поля не ниже четырех.

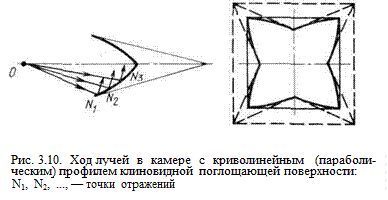Можно показать, что применение криволинейного (параболиче­ского) профиля клиновидной поглощающей полости (рис. 3.10) в ряде случаев также позволяет при меньшей глубине полости обес­печить ту же кратность отражений. Это позволяет несколько уменьшить необходимые габариты помещения.

Если, как показано на рис. 3.10, критический луч испытывает, например, не менее двух переотражений в полости, то и осталь­ные лучи испытывают не менее двух переотражений. При этомN₁N₂<N₂N₃при ÐN₁ON₂ = ÐN₂ON₃. Таким образом, используя простые геометрические соображения, удается в камере заданных габаритов сконструировать поглощающие полости, обеспечиваю­щие n-кратное переотражение поля от поглощающего материала. Однако это не означает, что таким образом удается в п раз пони­зить порядок остаточного поля в безэховой зоне. Существенные поправки вносит дифракция на изломах поверхности. Для пра­вильного формирования поглощающей поверхности безэховой ка­меры, выбора числа и формы рассеивателей необходим учет ди­фракционных полей и их зависимости от поглощающего мате­риала.

Расчет пирамиды

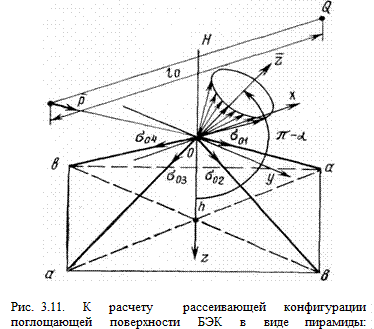
При использовании рассеивающих конфигураций в виде пира­мид необходимо обеспечить, чтобы в безэховую зону не попадало поле, рассеянное ребрами пирамиды, примыкающими к ее вер­шине. В противном случае порядок рассеянного поля определялся бы рассеянием на клиновидном ребре и использовать пирамиды вряд ли было бы целесообразно.

Как известно, поле, рассеянное клиновидным ребром при на­клонном падении на него плоской волны, имеет вид конуса ди­фракционных лучей [81]. Оси конусов совпадают с ребрами пи­рамиды, а угол образующей конуса равен углу между единичным вектором рпадающего на вершину О луча и единичным вектором ребра d_0i (рис. 3.11):

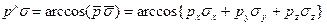(3.60)

или в сферических координатах q и j

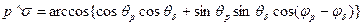. (3.61)

Пусть вектор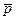лежит в плоскости ребер {s₀₁,s₀₃} пирамиды:

p={q_p,0}, s₀₁={a,0}, s₀₂={b,p/2}, s₀₃={a,p}, s₀₄={b,3p/2}, (3.62)

гдеa = arctg(a/h); b = arctg(b/h); (3.63)

а,-а и b, -b — размеры диагоналей основания пирамиды, опре­деляемые выражениями (3.42) и (3.43);

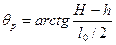; (3.64)

ctg q_р определен в п.п. 3.1 по допустимому минимальному размеру пространства распространения, а именно: ctgq_p= tgg.

Из (3.61) для рассматриваемого случая получим

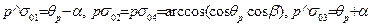(3.65)

Целесообразно угол a выбрать так, чтобы безэховая зона нахо­дилась вблизи оси конуса дифракционных лучей, рассеянных реб­ром s₀₃.

При симметричном расположении Р и Q относительно вершины пирамиды необходимо, чтобы a = q_p (3.66)

тогда 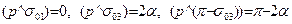. (3.67)

Поскольку a/tga = b/tgb, то

b = arctg(b×tga/a). (3.68)

А учитывая, что в соответствии с п.п. 3.2 b/a = sinq » sinq_P и соот­ветствующий (3.66) выбор угла а получим

b » arctg(sinq_p×tgq_p). (3.69)

Рассмотрим числовой пример. В п.п. 3.1 было показано, что при применении звездообразного просвета искажения —40 дБ могут быть достигнуты при tgg = 0,5. q_p= 90-26,5° = 63,5°, тогда в соответствии с (3.66) и (3.67) a = 63,5°; b = 60,88°. Углы между ребрами и образующей конуса дифракционных лучей будут

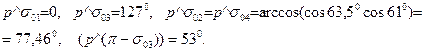
Так определяется ориентация ребер и граней пирамиды и сово­купность дифракционных лучей от ребер, примыкающих к верши­не. Определив а или b как большую или малую полуось эллипсов m-зоны Френеля бликующей области, которую надо исключить, мы определим также и линейные размеры пирамидальной рассеи­вающей конфигурации.

Полезно изобразить конуса дифракционных лучей от ребер пирамиды, примыкающих к ее вершине, зону излучения и безэховости в системе координат q и j. Для этого заметим, что в систе­ме координат х, у, z, связанной с конусом дифракционных лучей от ребра, уравнение конуса

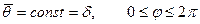. (3.70)

Система х, у, z для ребер s₀₁ и s₀₃ образовалась поворотом х, у, z относительно оси y на угол a, а для ребер s₀₂ и s₀₄ поворотом относительно оси x на угол b. Тогда в первом случае

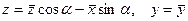, (3.71)

а во втором

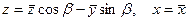, (3.72)

Или в сферических координатах единичного вектора для ребер s₀₁ и s₀₃

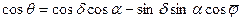
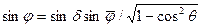. (3.73)

Для ребра s₀₁ d = d₀₁= arcos(ps₀₁), a₁ = a;

для ребра s₀₃ d = d₀₃= arcos(ps₀₃), a₃ = p-a;

для ребер s₀₂ и s₀₄

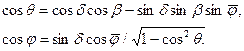(3.74)

Причем для ребра s₀₂ d = d₀₂= arcos(ps₀₂), b₀₂ = b для ребра s₀₄ d = d₀₄= arcos(ps₀₄), b₀₄ = b. Выражения (3.73) и (3.74) позволяют построить конуса дифракционных лучей от ре­бер пирамиды в координатах q и j, связанных с ее осью.

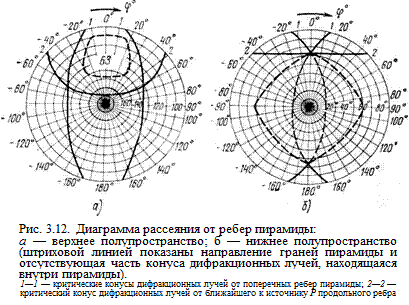
На рис. 3.12 в координатах q и j представлены конуса ди­фракционных лучей от ребер пирамиды, их положения относи­тельно безэховой зоны (БЗ)и зоны излучения. Такие диаграммы позволяют оценить правильность выбора геометрии рассеивающей конфигурации. На рис. 3.12, а изображено полупространство 90° £ q £ 180° над пирамидой, содержащее точку излучения Р. Точки пересечения конусов дифракционных лучей определяют на­правления отражений от граней (s₀₃, s₀₂) и (s₀₃,s₀₄) пирамиды. Видно, что имеется часть пространства, свободная от дифракцион­ных лучей, рассеянных ребрами, прилегающими к вершине пира­миды. В ней и располагается безэховая зона (БЗ).

На рис. 3.12, б изображено полупространство 0° £ q £ 90^o, со­держащее пирамиду. Направление граней пирамиды и отсутствую­щие части конусов дифракционных лучей внутри объема пирами­ды обозначены штриховыми линиями. Видно, что направ­ление отражений от граней (s₀₁, s₀₂) и (s₀₁,s₀₄) в данном приме­ре совпадает с ребром пирамиды s₀₁. В двух других точках пере­сечения линий 1 и 2 находятся отражения от граней (s₀₃, s₀₂) и (s₀₃,s₀₄).

Итак, геометрический расчет позволяет сформировать зоны интенсивных отражений в безэховой камере. Исходя из этого, по его результатам выбираются размеры рассеивающих конфигура­ций. Причем в случае применения клиновидных рассеивающих конфигураций их геометрия определяется по результатам иссле­дования полей, отраженных от граней клина, исходя из условий непопадания этого поля в безэховую зону и обеспечения n-крат­ных переотражений на поверхности камеры.

Для пирамидальных рассеивателей геометрический расчет фор­мы обеспечивает непопадание в безэховую зону также и дифрак­ционного поля от ребер, примыкающих к вершине пирамиды.