До виконання лабораторної роботи

1. Мета роботи.

2. Що таке коливальний контур та як відбуваються на ньому гармонічні коливання.

3. Записати та пояснити диференціальне рівняння згасаючих коливань у коливальному контурі.

4. Записати та пояснити рівняння, яке є розв’язком диференціального рівняння згасаючих коливань.

5. Чому дорівнює амплітуда згасаючих коливань?

6. Як можна визначити циклічну частоту згасаючих коливань?

7. Чому дорівнює власна частота згасаючих коливань?

8. Як можна отримати формулу періоду власних коливань (формулу Томсона)?

9. Запишіть та охарактеризуйте формулу періоду згасаючих коливань.

10. Що таке логарифмічний декримент згасання?

11. Який опір коливального контуру буде критичним?

12. Які коливання називають аперіодичними?

13. Що таке добротність коливального контуру?

Контроль запитання для захисту лабораторної роботи

1. Яким способом було одержано точне значення періоду згасаючих коливань?

2. Як наближено можна одержати період згасаючих коливань?

3. Як практично був виміряний коефіцієнт згасання і логарифмічний декримент згасання в цій лабораторній роботі?

4. Яке значення добротності коливальної системи було одержано в цій роботі?

5. Наведіть приклади суттєвих втрат енергії в коливальній системі?

6. Як можна розрахувати відносну та абсолютну похибки вимірювання періоду коливань в цій роботі?

Лабораторна робота № 4.5

Визначення частоти

Коливань мультивібратора

Мета роботи:вивчити стоячі хвилі в натягнутій струні та визначити частоту коливань мультивібратора.

Прилади і матеріали:мультивібратор (генератор імпульсів), електромагнетний збуджувач, струна, динамометр, лінійка, камертон, гвинт регулювання натягу струни, з'єднувальні провідники.

Теоретичні відомості

Рівняння плоскої біжучої хвилі, що поширюється в довільному середовищі зі швидкістю в додатному напрямку осі, має вигляд

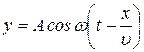, (1)

де у - зміщення коливної точки з координатою х в момент часу t, A - амплітуда зміщення, ω - циклічна частота коливань.

Рівняння будь-якої хвилі є розв'язком диференціального рівняння, що називається хвильовим. Щоб знайти вигляд хвильового рівняння, зіставимо другі частинні похідні за координатою х та часом t від функції (1):

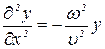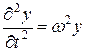; . (2)

Прирівнюючи праві частини рівнянь (2), легко отримуємо шукане хвильове рівняння:

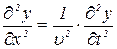, (3)

яке описує хвилю, що поширюється в напрямку осі ох зі швидкістю υ.

Розглянемо тепер коливання гнучкої однорідної струни. Вважатимемо, що струна здійснює малі поперечні коливання, тобто рух її точок відбувається біля положення стійкої рівноваги. Виділимо елемент струни довжиною Δl, показаний на рис.1. Проекція на вісь оу сили натягу струни Т, що діє на елемент Δl в точці з координатою х, для малих кутів а може бути записана:

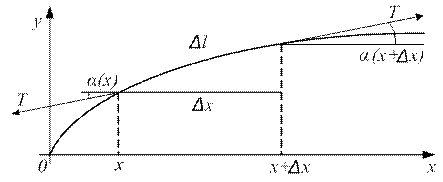
Рис. 1

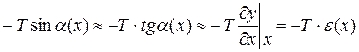, (4)

Аналогічно для точки струни з координатою х + Δх маємо:

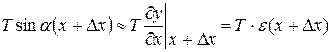. (5)

Сума проекцій (4) і (5) є тією силою, що приводить в рух елемент Δl

вздовж осі оу. При малих коливаннях Δy<<Δx (рис.1) і довжина елемента

струни Δx Δl, а його маса Δm=τ∙Δx, де τ - лінійна густина струни

За другим законом Ньютона

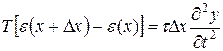, (6)

де 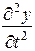– прискорення елемента струни. Очевидно, вираз (6) можна переписати у вигляді

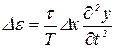. (7)

Розділивши (7) на Δx, перейдемо до границі при :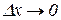

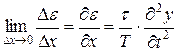. (8)

Повертаючись у (8) до явного вигляду відносної деформації струни 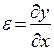остаточно матимемо:

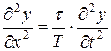. (9)

Рівність (9) є диференціальним рівнянням коливань струни. Прирівнюючи вирази (9) і (3), бачимо, що швидкість поширення хвилі в струні визначається формулою

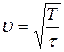. (10)

Як відомо, при додаванні когерентних хвиль виникає явище інтерференції, що полягає у посиленні коливань в одних точках і послабленні ­– в інших, особливий випадок інтерференції спостерігається при накладанні двох зустрічних плоских хвиль з однаковою амплітудою. Коливальний процес, що виникає при цьому, називається стоячою хвилею. Розглянемо виникнення стоячих хвиль у натягнутій струні.

Нехай вздовж струни в додатному напрямку осі поширюється попе-речна хвиля (див. рис.1)

,

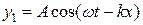де 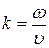- хвильове число. При відбитті даної хвилі від кінця струни утворюється зустрічна хвиля

,

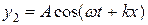що поширюється у від'ємному напрямку осі ох. Якщо відбиття повне, тобто амплітуди падаючої і відбитої хвиль однакові, від накладання таких хвиль утворюється стояча хвиля.

Скориставшись тригонометричною формулою додавання косинусів

,

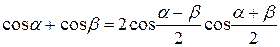отримаємо рівняння стоячої хвилі:

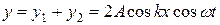. (11)

Згідно з (11), кожна точка струни, що визначається координатою х, здійснює гармонічне коливання з циклічною частотою ω та амплітудою A_cm=|2Acos kx| .

Точки, яким відповідає нульова амплітуда, називаються вузлами.

Очевидно, для вузлів 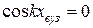, звідки ,

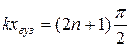n=0;± 1;±2…

Виразивши хвильове число через довжину хвилі λ, знайдемо корди-нати вузлів:

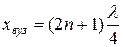. (12)

Точки, що коливаються з максимальною амплітудою, називаються пучностями. Для пучностей

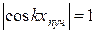, kx_пуч=nπ, n=0;± 1;± 2;…

Координати пучностей рівні

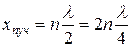. (13)

З рівностей (12) і (13) випливає, що відстань між сусідніми вузлом та пучністю дорівнює чверті довжини хвилі 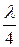, а між двома сусідніми вузлами та пучностями — половині довжини хвилі .

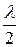Всі точки між двома сусідніми вузлами коливаються в однакових фазах. Вони одночасно проходять через положення рівноваги і одночасно досягають максимумів зміщень. При переході через вузол знак у змінюється на протилежний. Це означає, що при цьому фаза коливання стрибком змінюється на π. Однак це не призводить до порушення неперервності коливального процесу, оскільки стрибок фази відбувається при переході через точку з нульовою амплітудою.

Картина коливань в стоячій хвилі показана на рис.2. Лінії 1, 2, 3 зображають положення точок струни при коливаннях відповідно в моменти часу 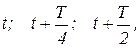де Т - період коливань струни, причому положення 1 і 3 є амплітудними. Стрілками показано напрямок руху, який виникає із зображених положень. Вузли немов би поділяють струну на автономні області, в яких здійснюються незалежні гармонічні коливання. Ніякої передачі руху від однієї області до іншої не відбувається, а отже, перенесення енергії через вузли не виникає. Саме тому таку хвилю називають стоячою.

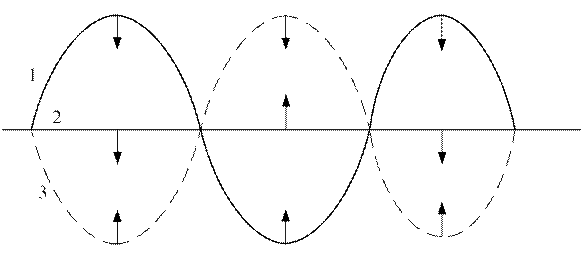
Рис.2

Зауважимо також, що оскільки швидкість точок струни, яка коливається в моменти часу, зображені на рис. 2 кривими 1 та 3, є найменшою, наше око завдяки інерції зору найчіткіше фіксує саме ці положення струни, що сприймаються при невеликих періодах коливань як одночасні.

Нехай розглянута вище струна закріплена з обох боків. В такому випадку на її кінцях можуть утворюватись лише вузли. Це означає, що на довжині струни l повинно вкладатись ціле число п півхвиль:

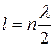. (14)

Врахувавши формулу швидкості (10) та визначивши довжину хвилі з (14), отримаємо вираз для частоти коливань струни

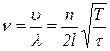, n=1,2,3… (15)

Опис установки

Установка для проведення експерименту (рис.3) складається з досліджуваної струни 1, що прикріплена з одного боку до камертона 2, який збуджується електромагнетом 3 при подачі на нього електричних коливань з мультивібратора 4. 3 іншого боку струна 1 зв'язана з динамометром 5, призначеним для вимірювання сили її натягу. За допомогою нитки 6, що утворює деякий кут зі струною 1, динамометр 5 зв'язаний з гвинтом регулювання натягу 7. Лінійка 8 служить для вимірювання зміни довжини Δl струни 1.

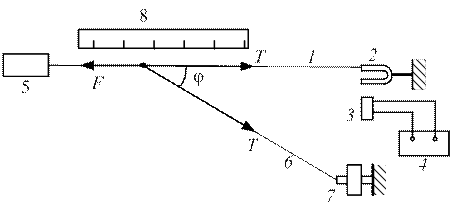
Рис. 3

Знайдемо робочі вирази для довжини струни l та сили її натягу Т. Очевидно, Δl =l₀ - l, де l₀ та l - відповідно довжина вільної та натягнутої струни; тому l = 1₀ - Δl. З рис.3 видно, що показ динамометра F та сила натягу струни Т пов'язані рівністю F = T + T cos φ, звідки .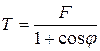

Таким чином, робоча формула для вимірювання частоти мультивібратора матиме вигляд:

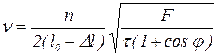. (16)

Хід роботи

1. Скласти установку згідно з рис. 3.

2. Після перевірки лаборантом правильності складання схеми послабити натяг струни до нульового, зафіксувати координати r кінця струни, з'єднаного з динамометром, виміряти початкову довжину струни l₀.

3. Включити генератор і ручкою регулювання виставити частоту, позначену міткою на шкалі.

4. Змінюючи натяг струни за допомогою регулюючого гвинта, домогтися утворення стійкої картини стоячої хвилі.

5. Зафіксувати координату r₂ кінця струни, зняти показання динамометра та визначити кількість n пучностей стоячої хвилі.

6. Довільним способом обчислити cosφ.

7. Не змінюючи частоту, виконати експеримент з іншими значеннями F та п (пп. 4-6) Результати вимірювань записати в таблицю