Лекция 3. Второе начало термодинамики

Тепловые двигатели и холодильники.

Есть определенная асимметрия между процессами взаимных превращений тепла и работы. В любом процессе с участием трения тепловая энергия легко получается за счет работы. Получить работу за счет тепловой энергии гораздо сложнее – такой процесс на основе паровой машины был осуществлен только в 1700 г. Всем известна также асимметрия в самопроизвольных процессах распространения тепла: теплота самопроизвольно всегда переходит от более нагретых тел к менее нагретым. Чтобы совершить обратный процесс, надо затратить работу. Причем чисто энергетически описанные выше факты не запрещены – они не противоречат закону сохранения энергии, или первому началу термодинамики. Запрещает такие процессы второе начало термодинамики. Оно было сформулировано несколькими учеными. Один из них – Клаузиус – сформулировал II начало так. Теплота не может сама собой переходить от менее нагретого тела к более нагретому. Другая формулировка – лорда

Кельвина – гласит: невозможен такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу. Эта формулировка подразумевает, что вся теплота, полученная в двигателе рабочим телом, не может быть превращена в работу – часть теплоты должна быть отдана холодильнику. Наиболее убедительно показал возможности превращения теплоты в работу в периодическом процессе французский инженер Сади Карно. Он рассмотрел идеальный обратимый цикл, известный с тех пор как цикл

Карно. Термодинамический процесс называется циклом, если в результате его протекания термодинамическая система возвращается в исходное состояние. Термодинамический процесс называется обратимым, если его можно осуществить в обратном направлении, не произведя при этом никаких изменений в окружающей среде. Рассмотрим, как осуществляется цикл Карно.

Пусть в цилиндре, оборудованном поршнем без трения, заключен газ, который служит рабочим телом. Имеется два источника тепла, поддерживаемых при определенных постоянных температурах: нагреватель с температурой Т₁ и холодильник с температурой Т_2. В начальный момент газ нагрет до температуры Т₁ и приведен в тепловой контакт с нагревателем. После этого газу дают возможность расширяться. На PV – диаграмме этот процесс изображается изотермой (при температуре Т₁) от точки 1 до точки 2. В точке 2 тепловой

P

Т₁

Т₂ 3

V₁V₄ V₂V₃ V

контакт с нагревателем прерывается, и газ продолжает расширяться по адиабате 2-3. На участке цикла 1-2-3 газ, расширяясь, производит работу. Чтобы вернуть его в исходное состояние (периодический процесс), его надо сжать, затратив внешнюю работу. Чтобы затраченная работа была меньше произведенной газом (т.е. чтобы в итоге получить выигрыш в работе), возврат осуществляется сначала по изотерме с температурой Т₂, меньшей Т₁; для этого рабочее тело приводится в тепловой контакт с холодильником (изотерма 3-4). В точке 4 тепловой контакт снова нарушается, и дальнейшее сжатие производится по адиабате 4-1. Рассмотрим подробнее отдельные участки цикла. На участке 1-2 газ расширяется при постоянной температуре Т₁, значит, он забирает от нагревателя некоторое количество тепла Q₁. На участке 2-3 газ продолжает расширяться, не получая тепла, значит, температура его падает. В точке 3 температура достигает температуры холодильника Т₁, и газ начинают сжимать, приведя в тепловой контакт с холодильником, т.е., не давая нагреваться. Значит, на этом участке газ отдает некоторое количество тепла Q₂ холодильнику. На участке

2-4 сжатие продолжается без обмена теплом (по адиабате), в результате температура газа растет, достигая исходного состояния. Мы рассмотрели цикл теплового двигателя, который называется прямым циклом. Из графика видно, что работа, произведенная газом, больше работы, затраченной на его сжатие, т.е. в итоге получен выигрыш в работе, который называется полезной работой.

Подсчитать эту работу можем, используя первый закон термодинамики для цикла.

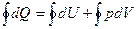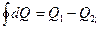
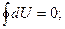
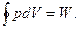; (20)

Отсюда следует, что L = Q₁ – Q₂..

Термическим к.п.д. цикла η_Т называется отношение полезной работы к количеству теплоты, полученной рабочим телом от нагревателя:

η_Т = L / Q₁ = (Q₁ – Q₂)/ Q₁ (21)

Далее, используя выражения для количества теплоты, участвующей в изотермическом процессе, и получив соотношение V₃/V₄ = V₂/V₁, получим

η_Т = L / Q₁ = (Т₁ – Т₂)/ Т₁ =1-Т₂/Т₁ (22)

Из (3) следует, что всегда ηТ < 1, и коэффициент полезного действия тем больше, чем меньше отношение абсолютных температур холодильника и нагревателя Т2/Т1.. Итак, существует нечто в Природе, ограничивающее в известном смысле наши возможности. Мы не можем изобрести вещество, которое, будучи использовано в тепловой машине, произвело бы за обратимый цикл работу больше допустимой. Это нечто и есть второй закон термодинамики.

Как мы видели на примере цикла Карно, работа может быть получена за счет теплоты, если только дать возможность теплоте переходить из области с более высокой температурой в область с более низкой. При этом только часть теплоты может быть преобразована в работу. В паровом двигателе в качестве рабочего тела используется перегретый пар, а высокая его температура достигается за счет сжигания угля, нефти или другого топлива. В двигателе внутреннего сгорания рабочим телом служит газ, образующийся при сгорании рабочей смеси (паров бензина с воздухом). Почему для работы этих двигателей необходима разность температур нагревателя и холодильника? Чтобы возвратиться к исходному состоянию (периодический циклический процесс), нужно произвести работу по сжатию рабочего тела, и если процесс сжатия будет происходить по той же изотерме, на сжатие будет затрачена та же работа, что газ произвел при расширении – никакого смысла в таком двигателе нет. Сжатие осуществляется по изотерме с низкой температурой, т.е. часть тепла, полученного при сжатии, отдается холодильнику. При отсутствии потерь на трение полезная работа равна разности количеств тепла, полученного от нагревателя и отданного холодильнику, Q₁ – Q₂.

Цикл Карно обратим: принцип действия холодильника состоит в обращении рабочих стадий теплового двигателя: первоначально нагретое рабочее тело расширяется по адиабате, затем приводится в контакт с холодильником и продолжает расширяться, забирая тепло Q₂ из холодильника. Возврат в исходное состояние происходит путем сжатия сначала по адиабате, а потом – по достижении температуры нагревателя – по изотерме, т.е. в итоге нагревателю отдано количество тепла Q₁, равное Q₂ +L, где L – произведенная работа.

Эффективность холодильного цикла оценивается отношением тепла, отнятого у холодильника, к произведенной работе сжатия: ε_х.ц. = Q₂/( Q₁ – Q₂).

Обратимый цикл Карно – это идеализация, на самом деле перетекание тепла от горячего источника к рабочему телу и от рабочего тела к холодильнику возможно только при наличии разности температур между этими телами. Любой процесс, связанный с переносом тепла, необратим – тепло не может самопроизвольно перетекать от холодного тела к горячему. Коэффициент полезного действия необратимого цикла всегда меньше, чем обратимого, поэтому полученная формула для термического к.п.д. есть лишь теоретический предел, к которому можно стремиться, улучшая конструкцию двигателя. Этот факт иногда трактуется как первая теорема Карно. Вторая теорема Карно утверждает, что термический к.п.д. теплового двигателя не зависит от используемого рабочего тела и является функцией только абсолютных температур нагревателя и холодильника. Это наиболее важное практическое следствие второго начала термодинамики.

Количественными выражениями качественных понятий о термодинамическом равновесии систем и изменении их состояний являются температура, внутренняя энергия, теплота и работа. Повторимся:

- Температура – это величина, введенная для того, чтобы устанавливать наличие (или отсутствие) термодинамического равновесия между системами. Для газа она является мерой средней кинетической энергии отдельных молекул.

- Внутренняя энергия – это сумма полных энергий составляющих систему структурных единиц (молекул).

- Теплота – это способ передачи энергии от одного тела к другому, если они находятся в тепловом контакте, и между ними существует разность температур.

- Работа – это тоже способ передачи энергии от одного тела к другому, но уже связанный с изменением положения тел, их перемещением (сжатие, расширение).

Для первого закона термодинамики существует его количественная формулировка 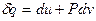, из которой следует, что в изолированной системе (к системе не подводится тепло и над ней не совершается работа) изменения состояния могут происходить лишь таким образом, чтобы сохранялась внутренняя энергия (du=0, u=const). Видимо, должно существовать и количественное выражение для второго закона термодинамики. Вернемся к обратимому циклу Карно.

(Q₁ – Q₂)/ Q₁ = (Т₁ – Т₂)/ Т₁ или Q₂ /Т₂ = Q₁ /Т₁

С учетом знаков (отданное тепло имеет знак «-«) для обратимого цикла Карно

это равенство может быть записано в виде суммы: 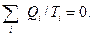Тем же Клаузиусом доказано, что любой другой обратимый цикл можно представить в виде суммы бесконечного числа циклов Карно, а значит в пределе сумма стремится к интегралу по замкнутому контуру: 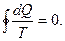Этот интеграл носит название интеграла Клаузиуса. В математике доказано, что если интеграл по замкнутому контуру равен нулю, то подынтегральное выражение есть полный дифференциал некоторой функции. Функция S, дифференциал которой 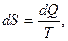называется энтропией термодинамической системы. Так как интеграл по замкнутому контуру равен нулю, то энтропия является функцией состояния системы, а не процесса, в результате которого она пришла к этому состоянию. Если рассматривать необратимый процесс, то интеграл Клаузиуса будет меньше нуля. Поэтому математическим выражением второго закона термодинамики является следующее: .

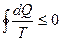Энтропия системы в произвольном термодинамическом процессе может как убывать, так и возрастать, изменение этой функции в основных процессах можно установить, используя определение энтропии и первый закон термодинамики.

- Изохорный: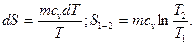

- Изобарный: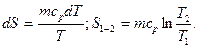

- Изотермический: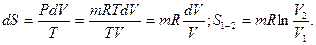

В адиабатном процессе энтропия постоянна, т.к. участвующее в процессе количество тепла равно нулю. Иначе этот процесс называется изоэнтропийным Состояние термодинамической системы можно также изобразить на

T-S- диаграмме. Цикл Карно на такой диаграмме будет изображен в виде прямоугольника, состоящего из двух прямых T = const. =T₁ , T = const. =T₂ – (изотермы) и перпендикулярных к ним прямых S = const. =S₁ , S = const. =S₂ – (адиабаты). Тогда количество теплоты, участвующей в процессе, вычисляется просто как площадь этого прямоугольника (dQ = TdS).

В обратимом цикле (как мы видели на примере цикла Карно) энтропия постоянна, как и в изолированной равновесной системе (dq=0). Рассмотрим изменение энтропии в необратимых самопроизвольных процессах. Пусть система изолирована (dq=0, Pdv =0), и состоит из двух частей с различными температурами Т₁>Т₂ . В системе начнется самопроизвольный необратимый процесс перетекания тепла из части с температурой Т₁ в часть с температурой Т₂. Изменение энтропии в результате этого самопроизвольного процесса dS = dS₁ + dS₂ = -dQ/T₁ + dQ/T₂ = dQ(1/T₂-1/T₁)>0. Таким образом, необратимый процесс в изолированной системе сопровождается ростом энтропии. Всякая неравновесная система с течением времени стремится к равновесному состоянию, в котором энтропия достигает максимума.

Самопроизвольные процессы возможны только в неравновесной изолированной системе, и протекают они до тех пор, пока энтропия не достигнет максимума.

Рассмотрим понятие энтропии с точки зрения порядка и беспорядка. Можно сформулировать два утверждения.

1. Беспорядок всегда самопроизвольно нарастает.

2. Увеличение энтропии сопровождается ростом беспорядка.

Это видно и на предыдущем примере: когда система состояла из двух частей с различными температурами, это было более упорядоченное состояние – два класса молекул с более высокими и более низкими энергиями. Процесс выравнивания температур привел к состоянию теплового равновесия – это не что иное, как беспрестанное хаотическое движение молекул, которые сталкиваются, обмениваются энергией, меняют направления, т.е. тепловое равновесие – это хаос. Со статистической точки зрения: микросостояние системы определено, если заданы положения и скорости составляющих ее микрочастиц; макросостояние определено, если определены макроскопические параметры системы. При этом огромное число микросостояний может соответствовать одному и тому же макросостоянию. Чем большим числом способов (числом микросостояний) может быть достигнуто данное макросостояние, тем более вероятно его осуществление – и тем больше энтропия в этом состоянии. Больцман связал энтропию макросистемы с числом микросостояний, которым это состояние может быть достигнуто: S = k lnW, где k – постоянная Больцмана, W – статистическая сумма (ее называют также термодинамической вероятностью). В рамках теории вероятностей второе начало термодинамики сводится к утверждению, что в Природе самопроизвольно происходят лишь те процессы, которые являются наиболее вероятными.

2.Уравнение состояния Ван-дер-Ваальса

Реальные газы отличаются от идеальных наличием сил взаимодействия между молекулами и наличием объема у самих молекул. Силы взаимодействия велики у газов, близких к переходу из газообразного состояния в жидкое, у молекул жидкости и твердых тел. Чем дальше состояние газа находится от области перехода в жидкое состояние, тем меньше силы взаимодействия между молекулами и тем ближе состояние газа к идеальному.

В первом приближении Ван-дер-Ваальс ввел две поправки, учитывающие отклонение газа от идеального состояния. Первая поправка учитывает конечный объем молекул: если давление увеличивать, объем газа уменьшается, и в пределе Р® ¥ для идеального газа v® 0; для реального газа минимальный объем будет определяться суммой объемов молекул и зазорами между ними. Поэтому Ван-дер-Ваальс ввел величину b – минимальный удельный объем, до которого можно сжать газ. Тогда уравнение состояния (для единицы массы газа) запишется как 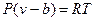или 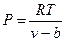. Отсюда следовало бы, что при одной и той же температуре давление у реальных газов выше, чем у идеальных.

Вторая поправка учитывает влияние сил взаимодействия между молекулами. Давление на стенку сосуда обусловлено ударами молекул о стенку. В реальном газе сила ударов меньше, чем в идеальном, т.к. молекулы, ударяющие в стенку, притягиваются соседними молекулами. Сила парных взаимодействий пропорциональна квадрату концентрации молекул, или квадрату плотности 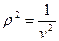. Тогда 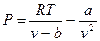, где a – вторая константа Ван-дер-Ваальса. Окончательно уравнение состояния записывается как

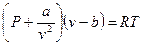(1)

Уравнение (1) и принято называть уравнением Ван-дер-Ваальса. Константы a и b различны для разных газов и определяются экспериментально.

3.Анализ уравнения Ван-дер-Ваальса.

В уравнении (1) раскроем скобки, сгруппируем слагаемые по степеням v и расположим их в порядке убывания степени:

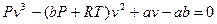(2)

Мы имеем уравнение третьей степени относительно переменной v. При заданных Р и Т оно должно иметь три корня. Возможны следующие ситуации:

1) все три корня действительны и различны;

2) все три корня действительны и равны между собой;

3) один корень действительный, два – комплексных; тогда реальное значение имеет один корень.

v

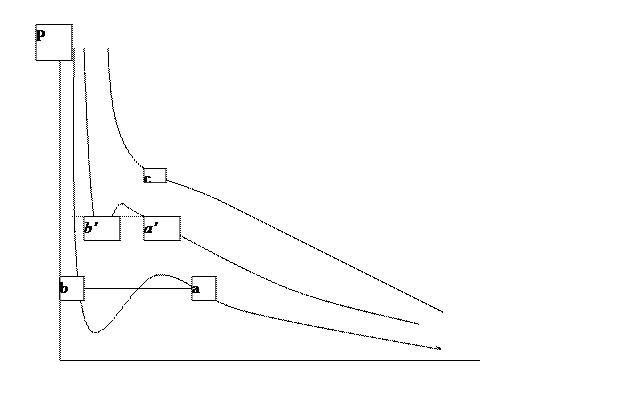
Рис.1 Изотермы Ван-дер-Ваальса

Рассмотрим решения на Р – v диаграмме. Начнем с низких температур. Изотерма при низких температурах имеет минимум и максимум, а решение для v– три действительных различных корня. Проследим переход от больших удельных объемов в сторону их уменьшения. При возрастании давления удельный объем уменьшается, и состояние газа (пара) приближается к состоянию жидкости. В точке а начинается конденсация пара. Волнообразное поведение изотермы между точками а, в не отражает реальной картины явления. На самом деле здесь имеется плато – давление остается постоянным при уменьшении удельного объема, система через влажный насыщенный пар переходит в жидкое состояние. Внутри отрезка а– в наблюдается равновесие жидкость – пар, в точке в пар полностью перешел в жидкость. Так как жидкость практически несжимаема, дальнейшее повышение давления не приводит к уменьшению объема. При переходе к более высокотемпературной изотерме область парообразования сужается, и при некоторой температуре изотерма имеет лишь точку перегиба – области парообразования и перехода в жидкое состояние не существует. При еще более высоких температурах изотермы реальных газов приближаются к изотермам идеального газа. Если соединить левые точки пересечения изотерм с изобарами и точку перегиба (b, b’, c), получим кривую, которая называется пограничной кривой жидкости; соединив правые точки пересечения изотерм с изобарами и точкой перегиба (a,a’,c), получим кривую, называемую пограничной кривой пара. Итак, для реального вещества P-v диаграмму можно разбить на три характерные области:

- область жидкого состояния (слева от пограничной кривой жидкости);

- область двухфазных состояний (влажного пара) – между пограничными кривыми жидкости и пара;

- область перегретого пара (справа от пограничной кривой пара).

Изотерма, имеющая точку перегиба, описывает состояние вещества при критической температуре. Это температура, при которой исчезают различия в физических свойствах между жидкостью и паром. Критическое состояние – это предельное состояние равновесной двухфазной системы, в котором обе сосуществующие фазы становятся тождественными по своим свойствам. Значения параметров состояния системы, соответствующие критическому состоянию, называются критическими: Р_кр, Т_кр, v_кр. При температуре, ниже критической, газ можно перевести в жидкое состояние при достаточно больших давлениях. Но если Т>Т_кр, никакое увеличение давления не приведет к переходу газа в жидкость. Именно поэтому долго не могли получить, например, жидкий кислород. Часто различают понятия «газ» и «пар». Вещество, находящееся в газообразном состоянии при температуре ниже критической, принято называть паром, а при температуре выше критической – газом. Приведем значения критических температур и давлений для некоторых веществ.

Вещество	t,0C	T,K	P,атм
CO2			72,8
O2	-118
N2	-147		33,5
H2	-239,9	33,3	12,8
He2	-267,9	5,3	2,3
Вода

При высоких температурах изотермы реального газа приближаются к изотермам идеального газа.

t, 0C

При определенных условиях вещество может перейти из жидкого состояния в твердое, т.е. вещество может находиться в трех фазовых состояниях, между которыми возможны переходы. Если вещество испытывает фазовый переход из твердого состояния в жидкое или из жидкого в газообразное, то этот процесс изменения фазы сопровождается передачей некоторого количества энергии.

Проследим, например, что происходит при равномерном нагреве 1 кг воды от температуры –20⁰С (когда она является льдом) до тех пор, пока весь лед не превратится в воду, которая при дальнейшем нагревании при t=100⁰C превратится в пар. Пусть все процессы происходят при атмосферном давлении.

Теплоемкость льда составляет 2,09 кДж/кг*град, поэтому для нагрева его от –20⁰С до 0⁰С потребуется примерно 42 кДж. При достижении 0⁰С теплота продолжает подводиться, но температура не растет, т.к. подводимая теплота идет на плавление льда. Количество теплоты, необходимое для превращения 1 кг вещества из твердого состояния в жидкое, называется теплотой плавления. Теплота плавления льда составляет 333,7 кДж/кг, именно такое количество теплоты надо подвести, чтобы превратить в воду 1 кг льда. При дальнейшем подводе теплоты (419 кДж) температура воды повышается вплоть до 100 ⁰С, после чего вода начинает превращаться в пар. Для превращения 1 кг воды в пар требуется

2256 кДж. Количество теплоты, необходимое для превращения 1 кг вещества в пар, называется теплотой парообразования (испарения). Значения теплоты плавления и теплоты парообразования называются также теплотой фазового перехода. При обратном переходе из пара в жидкое состояние или из жидкого состояния в твердое выделяется соответствующее количество теплоты фазового перехода. Количество теплоты, поглощаемое или выделяющееся при фазовом переходе, определяется по формуле Q = m*L, где m – масса вещества, L – теплота соответствующего фазового перехода. При низких давлениях вещество может переходить из твердой фазы в газообразную, минуя жидкую. Такой переход называется сублимацией. Например, углекислый газ, который в твердом виде называется сухим льдом, сублимирует даже при атмосферном давлении.

Для определения областей параметров состояния, соответствующих различным фазам вещества, обычно используется Р-Т диаграмма, называемая также фазовой диаграммой. На фазовой диаграмме можно выделить тройную точку, где возможно сосуществование всех трех фаз вещества. Тройная точка соответствует строго определенным значениям температуры и давления. Кроме того, на фазовой диаграмме можно выделить кривые равновесия, где сосуществуют фазы жидкость - пар, жидкость - твердое тело, твердое тело - пар. Примеры фазовых диаграмм даны на рисунках.

ВОДА

Твердое тело

газ

жидкость

Р,атм атмат

Критическая точка

Тройная точка

Т,0С

Дадим значения параметров тройных точек различных веществ.

Вещество	Температура, К	Давление, Па	Давление, атм
Вода	273,16	6,1*102	6,03*10-3
Углекислый газ	216,6	5,16*105	5,1
Аммиак	195,40	6,06*103	6,00*10-2
Азот	63,2	1,25*104	1,24*10-1
Кислород	54,4	1,52*102	1,50*10-3
Водород	15,8	7,03*103	6,95*10-2

Критическая точка для воды соответствует значениям параметров состояния: Т_кр = 374,15 ⁰С, Р_кр = 221*10⁵ Па (221 атм).