Турбуленттіліктің статикалық теориясын орташалау постулаттары

Статикалық тұрақты процестерге көптік бойынша орташалау уақыт бойынша орташалаумен сәйкес келеді.Яғни-

(t) = dr=const (1)

Жалпы жағдайда метеошамалардың алабы статикалық тұрақты болып табылмайды. Себебі көп жағдайда орташалаудан кейін алынған шамалар уақытқа тәуелді.Практикада Т - ның орнына Т_орт Т_п теңсіздігін қанағаттандыратын орташалаудың соңғы гипервалы Т таңдап алынады. Мұндағы Т_орт – орташаланған алқапқа тән өзгеру уақыты, ал Т_п- турбулеттілікке тән кезең.

Тұрақты орташа мәндерді есептеу тек атмосфералық ауытқудың спектрінде терең ауытқулар болған жағдайда ғана мүмкін. Жерге жақын және еркін атмосферада жүргізілген көптеген өлшеулердің нәтижелерінен алынған атмосфералық қозғалыстардың энергетикалық спектрін талдау Т шамамен 1 сағатқа тең екенін көрсетеді.Практикада бұл кезең 2-10 минутқа тең деп алынады.Орташалаудың соңғы кезеңінде шамаларды уақыт бойынша орташалау келесі түрде өрнектелуі мүмкін.

(t) = dr (2)

2 –ші теңдеу турбулентті атмосфераның гидротермадинамика орташаланған теңдеуін қорытындылау үшін қолданылатын орташалау постулаттарын алуға мүмкіндік береді.

35. Турбулентті атмосфера үшін теңдеулер жүйесі. Бастапқы және шектік шарттары.+

Атмосфера гидротермодинамикасының теңдеулер жүйесі:

1) Қозғалыс теңдеуі;

2) Үздіксіздік теңдеуі;

3) Күй теңдеуі;

4) Су буының тасымалдану теңдеуі;

5) Жылу ағынының теңдеуі.

1.Қозғалыс теңдеуі:

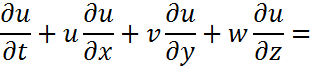
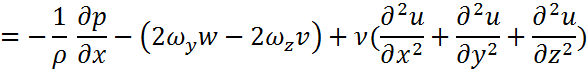
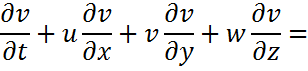
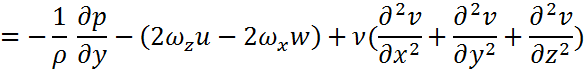
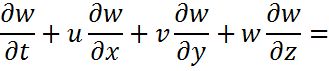
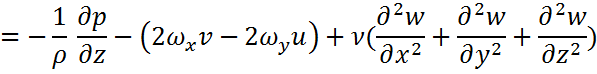
Қозғалыс теңдеуі қозғалыс мөлшерінің өзгеру заңының формуласы б.т. Мұнда кез келген дененің қозғалыс мөлшерінің бірлік уақытта өзгеруі сол денеге қосымша тең әсерлі күштерге теңелетінін ж/е сол теңескен күш/дің бағытында жүретінін айтады.

2.Үздіксіздік теңдеуі:

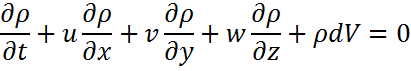
Атм/қ процес/дің динамикасын зерттеген кезде қысым алабы темп/а жылдамдығы ж/е басқа да сипаттаушылар қарастырылады. Бұл алқап/дың кеңістікте ж/е уақыт б/ша өзгеруін зерттеу үшін негізгі 3 сақталу заң/на негізделген сәйкесінше теңдеу/ді тұжырымдау керек: 1) салмақтың сақталу заңы; 2) қозғалыс заңының сақталу заңы;3) энергияның сақталу заңы;

Олардың біріншісі салмақтың сақталу заңы үздіксіз теңдеуін ж/е ауаның әр түрлі компонент/інің диффузиялар теңдеуін тұжырымдауға мүмкіндік береді. Бұл теңдеу/ді жазу үшін келесі түсінік/ге жүгінеміз: 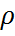тығыздықты қозғалып жатқан ауа салмағын қарастырамыз. а-сыбағалы, яғни бірлік салмаққа қатысты скалярлы шама болсын делік. Сонда бірлік көлем 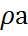-ға тең. Субстанциялар мөлшерінен тұрады.

3. Күй теңдеуі:

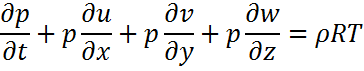
Атмосфералық ауаның физикалық күйін термодинамикалық жүйелер ретінде сипаттайтын негізгі параметрлер болып оның тығыздығы, қысымы ж/е абсолютті темп/сы ( 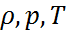) табылады.

Бойль-Марриот заңы қысым мен көлемді байланыстырады. Яғни, Т=const ж/е газдың тұрақты массасында m=const қысымның көлемге көбейтіндісі тұрақты болып қалады : pV=const

4.Су буының тасымалдану теңдеуі:

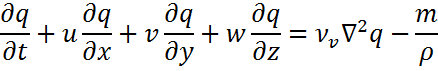
Мұндағы,

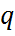– су буының салмақтық үлесі;

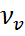– ауадағы су буының молекулалық диффузия коэффициенті;

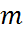– бірлік көлемді ауада бірлік уақыт ішінде қанығатын н/е буланатын су буының салмағы.

Су буы ауаның бір бөлігін құрайтын газ болғандықтан, оның тасымалдану жылд/ғы оның қозғалуының жылд/на тең.

5. Жылу ағынының теңдеуі:

Термодин/ң І бастамасының теңдеуі ішкі энергияның өзгеруін 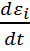, жылу ағынымен 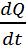ж/е сығылу күшінің 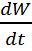жұмысымен байланыстырады:

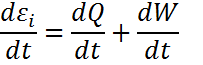
Жер атм/сына қатысты процесс/ге тән маңызды заңдылықты айта кету к/к. Атм/а үшін үлкен дәлдікпен квазистатистикалық жағдай (бөлшектің ішкі қысымы атм/да оны қоршап тұрған қысымға тең болуы қажет) 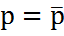теңдігі орындалуы к/к.

Ауаны идеалды газ ретінде қарастыруға болады:

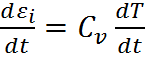ж/е