Распределение Больцмана. Барометрическая формула.

До сих пор мы не учитывали существование внешнего силового поля (например, гравитационного). В отсутствии поля молекулы газа равномерно распределяются по всему объему, т.е. плотность газа в объеме постоянна. Если действует силовое поле, то плотность частиц и давление газа будет функцией координаты точки f(x,y,z).

Получим закон изменения давления с высотой, при условии, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова.

Рассмотрим цилиндр сечением 1м², перпендикулярный поверхности Земли (рис.1.5.1). Разность давлений двух слоев, находящихся на различной высоте, равна весу газа между ними

.

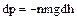На основании соотношения p=nkT исключаем n и получаем дифференциальное уравнение

.

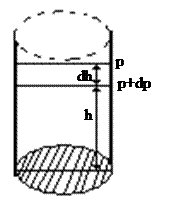
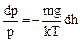Для решения этого уравнения интегрируем левую и правую части

Рис.1.5.1.

,

,

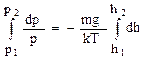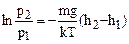или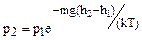

Это выражение называется барометрической формулой. Так как высота обозначается относительно уровня моря, где давление обозначим р₀, то это выражение может быть записано в виде

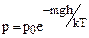, (1.5.2)

где р - давление на высоте h.

Если вернуться к соотношению p=nkT, то можно получить распределение концентрации молекул газа по высоте

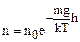. (1.5.3)

Барометрическая формула имеет простой физический смысл: молекул меньше там, где больше их потенциальная энергия. Увеличение потенциальной энергии молекулы в поле тяготения на величину mgh связано с работой сил поля

A=mgh.

Теперь можно определить потенциальную энергию молекулы, имеющей массу m и поднятую на высоту h

U(h)=mgh.

Тогда формула (1.5.2) примет вид 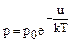. Этот вариант можно обобщить на случай, когда потенциальная энергия зависит не от одной, а от всех трех координат U(x,y,z):

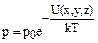(1.5.4)

Это один из вариантов распределения Больцмана для идеального газа во внешнем поле.

Аналогичную формулу имеем для концентрации молекул

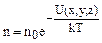(1.5.5)

Функция, характеризующая среднее число молекул, находящихся в данном состоянии, называют статистическим распределением.

При рассмотрении системы из множества частиц мы предполагаем, что частицы по каким-либо признакам отличаются друг от друга. Если две частицы поменяли местами, то такие состояния рассматриваются как различные.

Модель различных частиц называют моделью Максвелла-Больцмана, а полученную при этом статистику - статистикой Максвелла-Больцманан.

Пример8. На какой высоте h над поверхностью Земли атмосферное давление вдвое меньше, чем на ее поверхности? Считать, что температура воздуха 290°К, g=9,8 м/с², R=8,3×10³Дж×кмоль×к^-1, m=29 кг/кмоль, p/p₀=1/2.

Решение. Из барометрической формулы следует

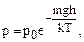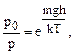или т.е. 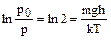, из полученного соотношения имеем

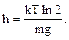поскольку k=R/N_A и m=m/N_A, получаем 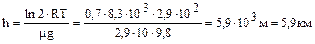- искомая высота.

Распределение Гиббса

Расширенная по сравнению с Максвеллом и Больцманом трактовка статистической физики была дана Гиббсом. В его трактовке задача заключается в вычислении средних значений физических величин. Вместо усреднения по времени в рамках одной системы рассматривается совокупность большого числа определенным образом неупорядоченных одинаковых систем. Замкнутая система определяется как система с постоянной энергией, постоянным числом частиц и постоянным объемом. Основополагающими понятиями в этом описании являются понятия ансамбля, совокупности частиц и фазового пространства.

Под фазовым Г-пространством понимают пространство всех обобщенных координат q и импульсов р. Микросостояние системы или ее фазаизображаются в этом пространстве точкой. При наличии n степеней свободы мы имеем пространство 2n-измерений.

Представим себе, что имеется N вариантов изучаемой системы, полностью адекватных в макроскопическом отношении: все они находятся в одинаковых внешних условиях, имеют одинаковый состав и строение. Такая условная совокупность тождественных, невзаимодействующих друг с другом систем называется ансамблем Гиббса. Различные системы ансамбля отличаются друг от друга микросостояниями. Будем предполагать, что в ансамбле представлены все возможные микроскопические состояния, совместимые с данными внешними условиями. С течением времени вследствие движения частиц микроскопические состояния сменяют друг друга.

В классической статистике каждое микросостояние системы характеризуется точкой. находящейся в объеме DpDq 6N-мерного пространства. Вероятность данного микросостояния системы, или вероятность того, что координаты и импульсы частиц находятся в заданном интервале Dx, Dp:

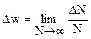, (1.6.1)

где N- полное число систем в ансамбле, DN- число микросостояний, изображаемых точками, лежащими внутри заданного объема.

Вероятность определенного состояния системы пропорциональна заданному фазовому объему DpDq и плотности распределения точек, изображающих состояния систем ансамбля в фазовом пространстве.

Функцией распределения (функцией состояния) f(p,q) называется плотность распределения (число точек в единице объема фазового пространства), отнесенных к полному количеству систем в ансамбле N.

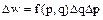(1.6.2)

Из определения вероятности следует, что должно иметь место условие нормировки

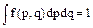(1.6.3)

Таким образом, функция распределения для некоторой изолированной (находящейся в термостате) системы имеет вид

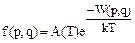, (1.6.4)

где W(p,q) - полная энергия системы, а коэффициент A(T) определяется из условия нормировки (1.6.2). Полученное распределение называется распределением Гиббса или каноническим распределением.

В случае квантовой статистики необходимо заменить непрерывное распределение различных состояний их дискретным набором. Характеристикой замкнутой системы служит энтропия. Каждому значению энергии W_i отвечает некоторая группа N(W_i) квантовых состояний (степень вырождения).

Так как все состояния с заданной энергией равновероятны, вероятность нахождения системы в одном из состояний с данной энергией

.

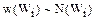Это микроканоническое распределение Гиббса. Оно показывает, что вероятность нахождения замкнутой системы в одном из состояний с данной энергией пропорциональна кратности его вырождения (см. библиографический список (3)).

Условие нормировки:

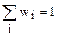(1.6.5)

Отсюда следует каноническое распределение Гиббса

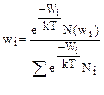(1.6.6)

При помощи распределения Гиббса можно вычислить среднее значение любой величины, зависящей от состояния системы. Состояние, отвечающее максимуму распределения Гиббса, является наиболее вероятным.