Эквивалентность характеристик обнаружения при корреляционной и фильтровой обработке

Поскольку на выходе оптимального фильтра в момент времени t = t_r + t₀ формируется корреляционный интеграл, отношения сигнал/шум по мощности γ или по напряжению q при фильтровой и корреляционной обработке эквивалентны, определяются исключительно отношением энергии сигнала Э_с к спектральной плотности шума N₀ и не зависят от формы сигнала:

.

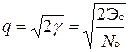На первый взгляд кажется, что можно по аналогии зафиксировать эквивалентность характеристик обнаружения при фильтровой и корреляционной обработке. Однако, эта эквивалентность обеспечивается только при определенном условии. Дело в том, что фильтр, обладая свойством инвариантности по времени запаздывания, «обслуживает» все элементы разрешения по дальности (времени запаздывания). Это означает, что на выходе порогового решающего устройства будут приниматься решения по всем элементам разрешения и вероятность лож­ного решения о наличии сигнала F_m будет возрастать по сравнению с вероятностью ложной тревоги F отнесенной к одному элементу разрешения, пропорционально числу элементов разрешения

.

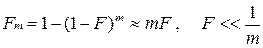В то же время при корреляционной обработке на выходе порогового решающего устройства будет приниматься решение только по одному элементу разрешения, соответствующему времени задержки опорного сигнала.

Поэтому условием эквивалентности характеристик обнаружения при корреляционной и фильтровой обработке является стробирование выхода фильтровой обработки в момент времени t = t_r + t₀ коротким δ-образным импульсом (рис. 5.7).

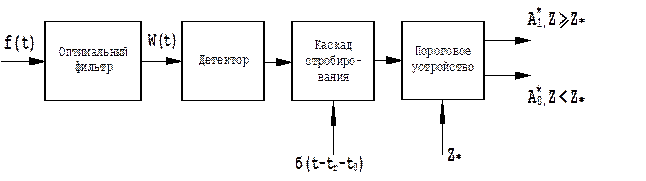Рис. 5.7. Схема фильтрового обнаружителя, эквивалентного корреляционному обнаружителю.

ОПТИМАЛЬНЫЕ ФИЛЬТРЫ ТИПОВЫХ ОДИНОЧНЫХ СИГНАЛОВ

Оптимальный фильтр простого прямоугольного радиоимпульса.

Квазиоптимальные фильтры.

Импульсная характеристика такого фильтра, т.е. его отклик на дельта-функцию, представляет собой простой прямоугольный радиоимпульс (рис. 6.1). Устройство с такой импульсной характеристикой показано на рис. 6.2. Оно состоит из радиоинтегратора, прямого и задержанного каналов (t_з =Т₀) и устройства вычитания. Под действием дельта-образного импульса на выходе радиоинтегратора формируется непрерывное колебание на радиочастоте. На выходе задержанного канала это колебание смещается по времени на длительность сигнала Т₀. В результате на выходе устройства вычитания формируется радиоимпульс, длительность которого определяется задержкой t_з =Т₀. Процесс формирования отклика такого устройства на дельта-функцию показан на рис. 6.3. Формирование отклика оптимального фильтра на принятый сигнал показано на рис. 6.4, откуда следует, что огибающая сигнала на выходе фильтра является треугольной, т.е. определяется корреляционной функцией закона модуляции простого прямоугольного радиоимпульса.

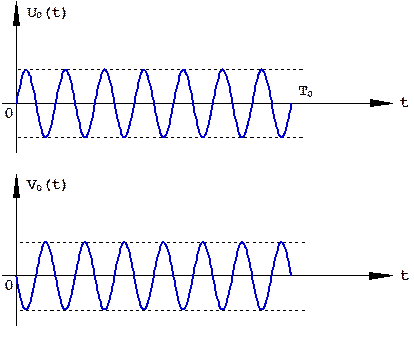
Рис. 6.1. Простой прямоугольный радиоимпульс и импульсная характеристика его оптимального фильтра

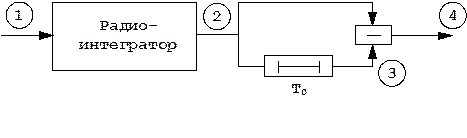
Рис. 6.2. Оптимальный фильтр простого прямоугольного импульса

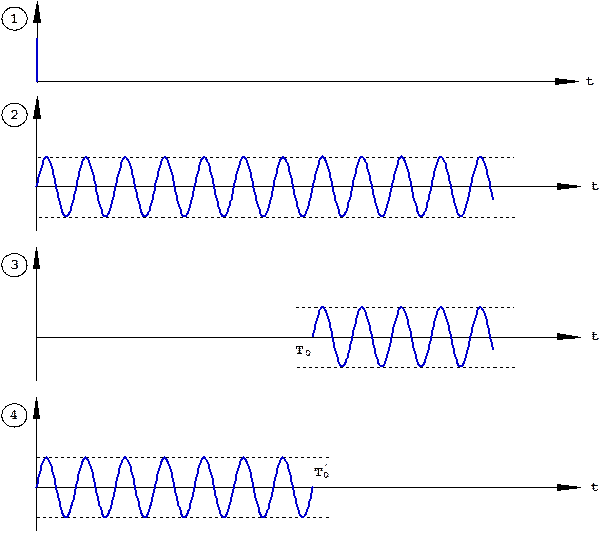
Рис. 6.3. Формирование отклика оптимального фильтра (рис. 6.2) на дельта-функцию

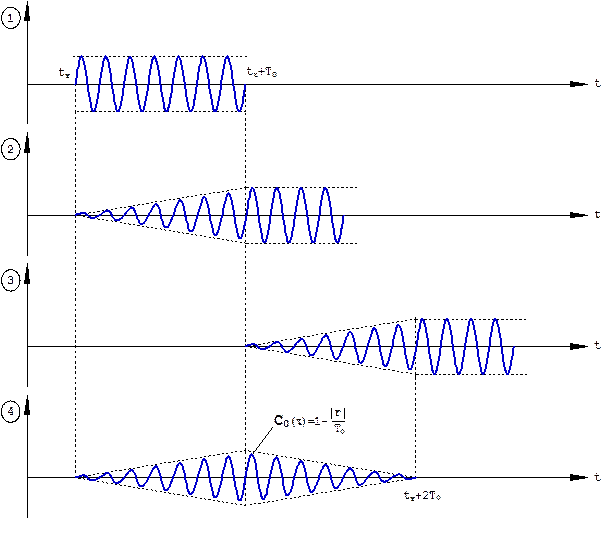Рис. 6.4. Формирование отклика оптимального фильтра (рис. 6.2) на принятый сигнал

Обычно оптимальные фильтры простых прямоугольных радиоимпульсов не используются ввиду возможных погрешностей из-за неидеальности радиоинтегратора и неидентичности коэффициентов прямого и задержанного каналов.

В 1946 году В.И. Сифоров развил теорию квазиоптимальной фильтрации с использованием фильтров, определенным образом согласованных только по полосе пропускания с шириной спектра сигнала, но рассогласованных по форме амплитудно-частотной характеристики с амплитудно-частотным спектром сигнала. Рассмотрим два примера квазиоптимальных фильтров.

Пример 1. Фильтр с использованием одиночного колебательного конура, частотная характеристика которого определяется выражением:

.

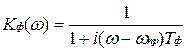Его импульсная характеристика, являясь обратным преобразованием Фурье, определяется выражением

.

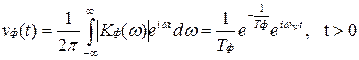Полоса пропускания фильтра обратно пропорциональна удвоенной постоянной времени фильтра

.

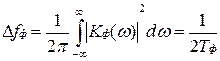Фильтр настроен на промежуточную частоту ω_пр, т.к. предполагается, что спектр сигнала смещен на эту частоту (рис. 6.5).

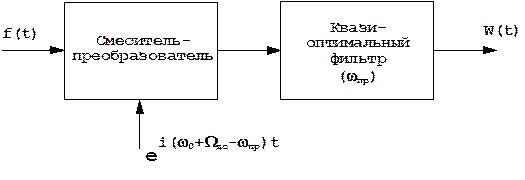
Рис. 6. 5. Смещение спектра и квазиоптимальная фильтрация сигнала на промежуточной частоте

При этом сигнальная составляющая напряжения на выходе фильтра может быть представлена в следующем виде:

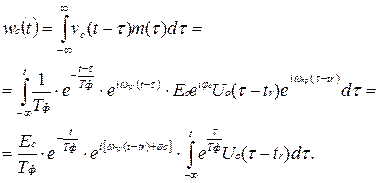
Сигнальная составляющая достигает максимального значения в момент t = t_r + Т₀

.

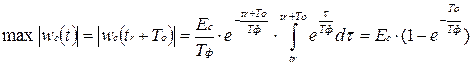Мощность шума на выходе фильтра (при нормированной АЧХ) может быть найдена как произведение спектральной плотности входного шума и полосы пропускания фильтра

.

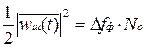Отношение амплитуды сигнала к среднеквадратичному значению шума на выходе фильтра оказывается равным

.

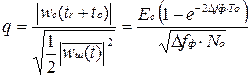Аналогичное отношение на выходе оптимального фильтра равно

.

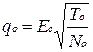Отношение q/q₀ характеризует эффективность неоптимальной фильтрации по сравнению с оптимальной:

.

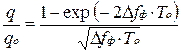Зависимость q/q₀ от Δf_фТ₀ показана на рис. 6.6. При Δf_фТ₀ = 0,65 отношение q/q₀ достигает максимального значения:

.

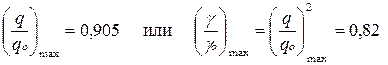Следовательно, одиночный колебательный контур, полоса пропускания которого определенным образом согласована с шириной спектра сигнала

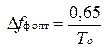
является квазиоптимальным фильтром простого прямоугольного радиоимпульса, поскольку потери в отношении сигнал/шум по мощности по сравнению с оптимальным фильтром составляют 18%, т.е. не превышают 1 дБ (26%).

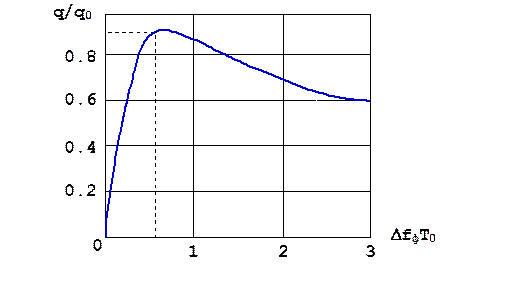
Рис. 6. 6. Эффективность фильтра с использованием одиночного колебательного контура, как квазиоптимального фильтра простого прямоугольного радиоимпульса

Пример 2. Фильтр с прямоугольной АЧХ, построенный на «парах» или "тройках" взаимно расстроенных контуров:

.

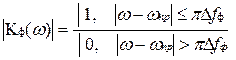Спектр принятого сигнала, смещенный на промежуточную частоту, определяется выражением

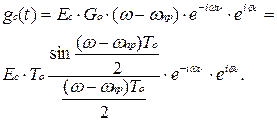
Отклик фильтра с прямоугольной АЧХ на принятый сигнал можно представить в следующем виде:

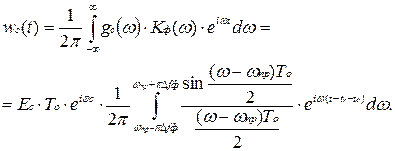
Сигнальная составляющая достигает максимального значения в момент

t = t_r + t₀ :

,

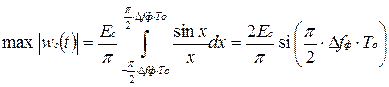где 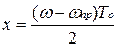- новая переменная интегрирования; 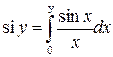-интегральный синус.

Мощность шума на выходе фильтра равна

.

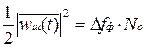Отношение амплитуды сигнала к среднеквадратичному значению шума на выходе фильтра при этом определяется выражением

.

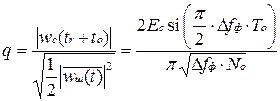Отношение q/q₀, характеризующее эффективность неоптимальной фильтрации по сравнению с оптимальной, оказывается равным

.

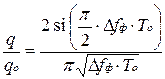Зависимость q/q₀ от Δf_фТ₀ показана на рис. 6.7. При Δf_фТ₀ = 1,37 отношение q/q₀ достигает максимального значения:

.

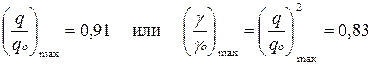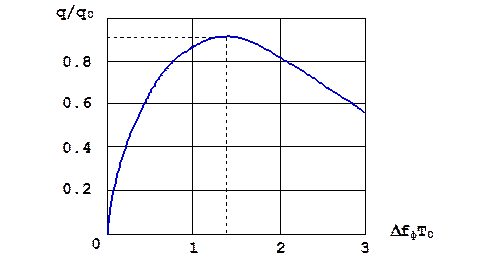
Рис. 6.7. Эффективность фильтра с прямоугольной АЧХ, как квазиоптимального фильтра простого прямоугольного радиоимпульса

Следовательно, фильтр с прямоугольной АЧХ, полоса пропускания которого определенным образом согласована с шириной спектра сигнала

,

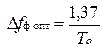является квазиоптимальным фильтром простого прямоугольного радиоимпульса, поскольку потери в отношении сигнал/шум по мощности по сравнению с оптимальным фильтром составляют 17% т.е. не превышают 1 дБ.