Изотермы Ван-дер-Ваальса. Связь критических параметров с постоянными в уравнении Ван-дер-Ваальса

Законы идеального газа являются приближенными, а отступления от этих законов обусловлены существенным отличием свойств идеального и реального газов. В отличие от идеального газа между молекулами реального газа существуют силы взаимодействия, которые на малых расстояниях между молекулами носят характер отталкивания, а на достаточно больших расстояниях между молекулами действуют силы притяжения. Кроме этого, молекулы реального газа не могут быть представлены как материальные точки. Молекулы реального газа имеют отличный от нуля собственный объем. Учет собственного объема и сил взаимодействия позволил получить уравнение состояния для реального газа.

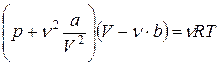, (1)

где a и b - поправки на внутреннее давление и собственный объем молекул реального газа, ν - число молей.

Теоретически полученное уравнение (1) называется уравнением Ван-дер-Ваальса.

Рассмотрим экспериментальные изотермы жидкости, пара и перехода жидкость – пар. На рисунке 1 показан теоретический график зависимости давления от объема для реального газа, который строится на основе анализа уравнения Ван-дер-Ваальса при помощи компьютерной модели.

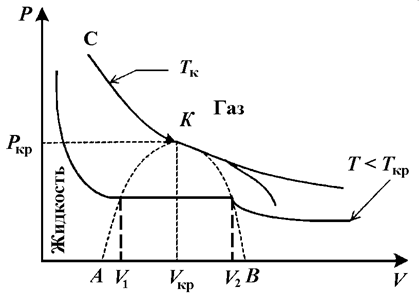Рисунок 1 - Изотермы реального газа

Кривая АК соответствует точкам начала кипения, кривая КВ – точкам конца кипения. Линия АКВ, которая отделяет зоны сосуществования пара и жидкости, называется бинодалью. Точки под бинодалью соответствуют равновесию жидкости и пара. В области АКВА пар является насыщенным. Равновесные участки изотерм в этой области являются изобарами. Видно также, что с ростом температуры точки начала и конца кипения сближаются и в точке К они совпадают. В этой точке исчезает различие между жидкостью и паром. В точке К резко возрастает коэффициент поглощения света. Этот процесс получил название критической опалесценции. Состояние термодинамической системы в точке К называется критическим. Критическому состоянию соответствует критическое давление p_кр , критическая температура T_кр и критический объем V_кр. При этом критическая изотерма в точке К имеет перегиб.

Между поправками уравнения Ван-дер-Ваальса a и b, критическим давлением p_кр, критической температурой T_кр и критическим молярным объемом V_кр0 в критическом состоянии существует следующая связь:

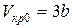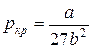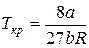, , . (2)

Действительно, в точке перегиба К критической изотермы первая и вторая производные от давления по объему равны нулю, т.е.

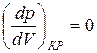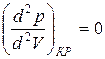и . (3)

Для доказательства соотношений 2 проанализируем уравнение Ван-дер-Ваальса для одного моля газа.

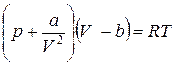. (4)

Из уравнения (4) определим давление.

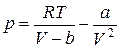. (5)

Далее найдем первую и вторую производные от давления по объему и приравняем полученные значения для критического состояния к нулю.

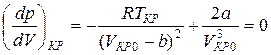. (6)

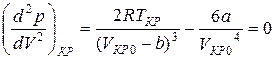. (7)

Из уравнений (6) и (7) получим:

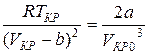. (8)

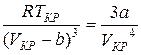. (9)

Разделив почленно соотношения (8) на (9), найдем критический объем:

.

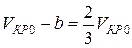Отсюда

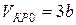. (10)

Подставляя уравнение (10) в соотношение (8), определим критическую температуру:

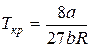. (11)

И, наконец, подставляя соотношения (10) и (11) в уравнение (5) для критического состояния, найдем критическое давление:

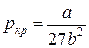. (12)