Находим радиусы стационарных орбит электронов

. Для атома водорода (Z=1) радиус первой орбиты электрона при n = 1, называемый первым боровским радиусом (а), равен

r₁ = a = 0,528 А. (4)

внутренняя энергия атома слагается из кинетической энергии электрона (Т = mv²/2) и потенциальной энергии взаимодействия электрона с ядром (U =-Ze²/(4pe₀r)),

При выводе формулы (5) учли формулу (1). Подставляя в (5) квантовые радиусы орбит электронов (3), получим, что энергия атома (которая равна энергии электрона, так как ядро атома неподвижно) может принимать только следующие дозволенные дискретные (квантовые) значения

где знак минус означает, что электрон находится в связанном состоянии. (В атомной физике энергия измеряется в электронвольтах, 1 эВ = 1,6×10^-19Дж).

Для описания длин волн λ четырех видимых линий спектра водорода И. Бальмер предложил формулу

где n = 3, 4, 5, 6; b = 3645,6 Å.

Спектральные серии водорода — набор спектральных серий, составляющих спектр атома водорода. Поскольку водород — наиболее простой атом, его спектральные серии наиболее изучены. Они хорошо подчиняются формуле Ридберга:

,

где R = 109 677 см⁻¹ — постоянная Ридберга для водорода, — основной уровень серии. Спектральные линии возникающие при переходах на основной энергетический уровень называются резонансными, все остальные — субординатными.

Модель атома Н. Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта модель атома внутренне противоречива: с одной стороны, применяет законы классической физики, с другой — основывается на квантовых постулатах. С ее помощью удалось объяснить основные закономерности в спектрах атомов водорода и водородоподобных систем и вычислить частоты спектральных линий. Оставалось, однако, неясным, от чего зависит интенсивность излучения тех или иных частот. Без ответа остался вопрос, почему совершаются те или иные переходы. Серьезным недостатком модели атома Бора была невозможность описать с ее помощью атом гелия — один из простейших атомов, непосредственно следующий за атомом водорода.

Билет24

1, Гармонической волной называется линейная монохроматическая волна, распространяющаяся в бесконечной динамической системе. В распределённых системах общий вид волны описывается выражением, являющимся аналитическим решением линейного волнового уравнения

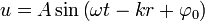
где 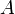– некоторая постоянная амплитуда волнового процесса, определяемая параметрами системы, частотой колебаний и амплитудой возмущающей силы; 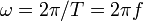– круговая частота волнового процесса, 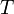– период гармонической волны, 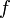– частота; 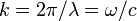– волновое число, 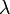– длина волны, – скорость распространения волны; 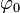– начальная фаза волнового процесса, определяемая в гармонической волне закономерностью воздействия внешнего возмущения.

2, Вектор Умова-Пойнтинга S= [ExH] - вектор, направление которого совпадает с направлением распространения энергии в электромагнитной волне, а модуль |S| равен потоку энергии.

3, Интерференция света — перераспределение интенсивности света в результате наложения(суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

4, оказывается находим - связь разности фаз колебаний с оптической разностью хода по формуле:

радиан.

5, Таким образом, размер отверстия, выраженный в количестве открытых зон Френеля, зависит не только от расстояний r и s, но и от длины волны l источника света. Можно показать, что если число открытых зон Френеля нечетное, то в т. P будет наблюдаться светлое пятно, если же открыто четное число зон Френеля, то в центре картины будет темное пятно.

6, Энергия фотона:

где ν — частота, λ — длина волны света, h = б,626·10^-34 Дж·с = 4,136·10^-15 эВ ·с,
— постоянная Планка,
ω — циклическая частота.