Определение момента инерции махового колеса

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА ПО ИЗГИБУ ПЛАСТИНЫ

Цель работы:практическое изучение закона Гука.

Задача:определить практически модуль Юнга по изгибу стальной и бронзовой пластины.

Приборы и принадлежности: 1.Кронштейн с опорами

2.Скоба – 50г.

3.Часовой индикатор перемещений

4.Грузы: 10г – 1шт;

20г – 2шт;

50г. – 1шт

5.Стальная и бронзовая пластина

Краткая теория

Сила характеризует действие одного тела на другое. В результате этого воздействия тело может прийти в движение или деформироваться. Деформацией твердого тела называется изменение взаимного расположения частиц тела, которое приводит к изменению формы и размеров тела и вызывает изменение сил взаимодействия между частицами, т. е. возникновение напряжений. Деформируемыми являются все вещества.

Деформация может быть следствием теплового расширения, воздействия электрических и магнитных полей, а также внешних механических сил.

В твердых телах деформация называется упругой, если она исчезает после снятия нагрузки, и пластической, если она после снятия нагрузки не исчезает. Различают несколько видов деформации: деформация одноосного растяжения, деформация всестороннего сжатия, деформация кручения, деформация сдвига, деформация изгиба.

Внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая силой упругости. Силы упругости обусловлены взаимодействием между частицами (молекулами и атомами) тела и имеют электрическую природу.

Физическая величина, численно равная упругой силе 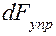, приходящейся на единицу площади 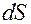сечение тела, называется напряжением:

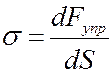
Английский физик Р. Гук экспериментально установил, что напряжение 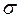при упругих деформациях тела прямо пропорционально его относительной деформации :

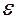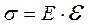, (1)

где 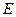- модуль Юнга (модуль упругости), величина которого определяется свойствами материала, из которого изготовлено тело. Например, ;

; ; .

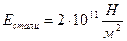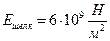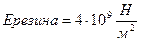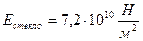Относительная деформация равна отношению абсолютной деформации 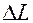к начальной длине :

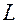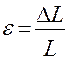(2).

Рассмотрим упругую деформацию одностороннего растяжения .(рис. 1 )

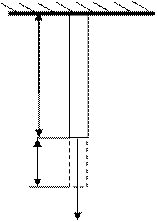К нижнему концу закрепленной проволоки длиной 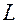и площадью поперечного сечения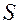

приложим силу 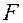, под действием которой

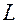проволока получит абсолютное удлинение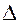

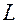
и в ней возникнет сила упругости .

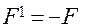По закону Гука напряжение 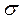, возникшее в

проволоке, прямо пропорционально относительной

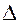
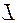деформации:

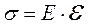(1) ,

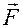отсюда модуль Юнга равен:

Рис. 1 Е = 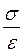(2)

Если положить, что 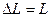, т.е. 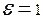, то 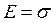, т.е. модуль Юнга численно равен напряжению, возникающему в упруго деформированном теле, при относительной деформации, равной единице.

Заменив в формуле (2) напряжение и относительное удлинение по формулам 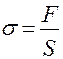и 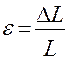, получим:

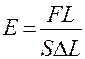(3)

Площадь поперечного сечения проволоки 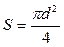(4), где 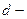диаметр проволоки.

Несмотря на большое разнообразие способов деформирования твердых тел все виды деформаций можно свести к суперпозиции двух видов – деформации одноосного растяжения и сдвига. В частности при деформации изгиба пластины, лежащей свободно на двух опорах и нагружаемой в центре грузом, внутри деформируемого образца происходит одноосное растяжение слоев, величина которого определяется значением нагрузки и материалом этого образца. Расчеты показывают, что применительно к изгибу, как способу деформирования тела (см. рис. 2), представляющего собой пластину, модуль Юнга можно рассчитать по формуле:

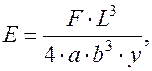(4)

где F – нагрузка, вызывающая прогиб пластины, Н;

L =0,114 м – расстояние между призмами (опорами);

а = 0,012 м – ширина сечения пластины;

b =0,0008м – толщина пластины;

y = значение прогиба, м.

Нагрузка рассчитывается по формуле:

F=(m_n-m₁)g

где m₁ – масса первого груза; m_n – масса n-ного груза; g – ускорение свободного падения.

Значение прогиба у определяется по формуле:

у=у_n-у_1,

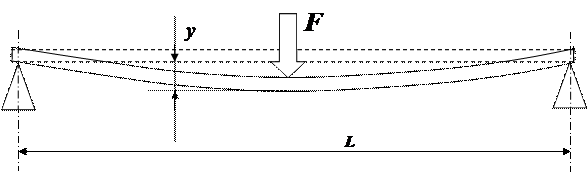Рис.2

Порядок выполнения работы

1. Установить одну из исследуемых пластин на призматические опоры.

2. Установить часовой индикатор таким образом, чтобы его наконечник коснулся пластины.

3. Подвесить скобу устройства нагружения образца посредине пластины.

4. Повесить на скобу груз массой m₁

5. По шкале индикатора определить значение прогиба пластины у₁.Снять груз.

6. Повесить на скобу груз массой m_2.

7. По шкале индикатора определить значение прогиба пластины у₂. Снять груз.

8. Повторить пункты 6 и 7 еще для нескольких грузов.

9. Данные измерений и расчетов по формуле (4) занести в таблицу.

№	m	y	E	ΔE	Есредн	ΔEсредн	Еист= Есредн± ΔEсредн

Контрольные вопросы

1.Что называется деформацией, виды деформаций?

2.Какими величинами характеризуют деформацию растяжения (сжатия)?

3.Как читается закон Гука и для каких деформаций он справедлив?

4.Какой физический смысл модуля Юнга?

Литература.

1. Детлаф А.А., Яворский Б.М., Милковская Л.Б. "Курс физики" ч.1.

2. Шубин А.С. "Курс общей Физики".

3. Грабовский Р.И. "Курс физики".

ЛАБОРАТОРНАЯ РАБОТА №2

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА

И СИЛЫ ТРЕНИЯ В ОПОРЕ

Цель работы:Закрепление теоретического материала по теме "Динамика вращательного движения твердого тела".

Задачи: Вычислить момент инерции махового колеса и силу трения в опоре.

Приборы и принадлежности: Прибор, состоящий из махового колеса, укрепленного на стене, масштабная линейка, штангенциркуль, секундомер, шнур с грузом.

Краткая теория

Твердое тело можно рассматривать как систему материальных точек, расстояние между которыми неизменно. Вращательным движением твердого тела называют такое движение, при котором все точки тела описывают окружности вокруг некоторой оси вращения. Если тело может вращаться вокруг неподвижной оси, то изменение его движения зависит от действующего на тело момента силы. Моментом силы 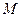относительно неподвижной оси называется векторная физическая величина, численно равная произведению силы 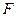на её плечо 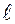, т.е. кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила:

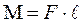(1)

Вращательное движение твердого тела характеризуется угловой скоростью 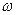и угловым ускорением .

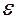Угловой скоростью вращения называется вектор 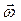, численно равный первой производной от угла поворота 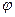радиуса-вектора по времени и направленный вдоль оси вращения так, что из его конца вращение видно происходящим против часовой стрелки:

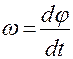(2)

Угловым ускорением называется вектор 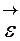, равный первой производной от угловой скорости по времени:

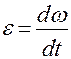(3)

Моментом инерции материальной точки относительно оси вращения называют скалярную физическую величину, численно равную произведению массы этой точки на квадрат расстояния её до оси вращения:

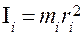
(4)

Момент инерции твердого тела равен сумме моментов инерций материальных точек:

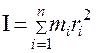(5)

Зависимость углового ускорения 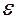от момента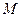

действующей на тело силы и момента инерции

тела выражается вторым законом Ньютона

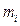для вращательного движения (основным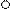

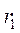законом динамики вращательного движения):

Рис. 1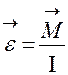(6) и читается:

Угловое ускорение тела при его вращении вокруг неподвижной оси прямо пропорционально вращающему моменту М силы, действующей на тело, и обратно пропорционально моменту инерции І тела относительно этой оси.

Если сопоставить законы поступательного и вращательного движений, легко сделать вывод, что момент инерции во вращательном движении выполняет ту же роль, что и масса в поступательном движении, так момент инерции характеризует инертность тела во вращательном движении.

Вращающееся тело обладает кинетической энергией:

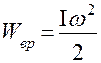(7)

Момент инерции махового колеса и силу трения вала в опоре можно определить при помощи прибора, изображенного на рисунке 2.

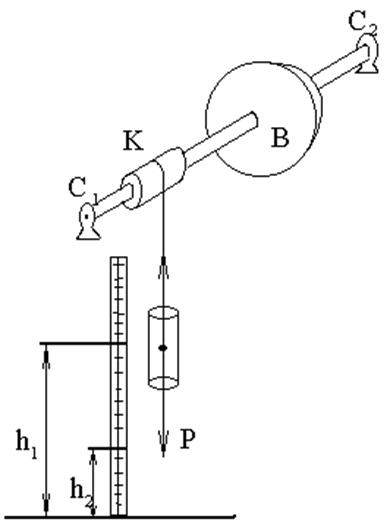
Рис. 2

Прибор состоит из махового колеса B, укрепленного на валу. Вал установлен на шарикоподшипниках 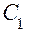и 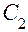. Маховое колесо приводится во вращательное

движение грузом Р. Груз Р на какой - то высоте 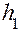обладает потенциальной энергией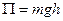 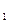, где 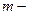масса груза.

Если предоставить возможность грузу падать, то потенциальная энергия 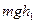груза перейдет в кинетическую энергию 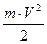поступательного движения груза, кинетическую энергию вращательного движения 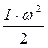прибора и в работу

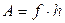по преодолению силы трения 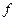в опоре. По закону сохранения энергии

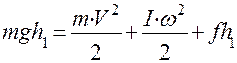(8)

Движение груза - равноускоренное без начальной скорости, поэтому ускорение а и скорость 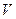соответственно равны:

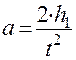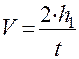; , (9)

где t - время опускания груза с высоты h_1.

Найдем угловую скорость махового колеса по формуле:

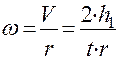, (10)

где 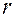- радиус вала, на который намотана нить.

Сила трения 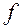вычисляется следующим образом. После опускания груза колесо, вращаясь по инерции, поднимает груз на высоту 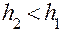, и потенциальная энергия груза на высоте 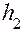будет равна .

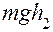Уменьшение потенциальной энергии при подъеме груза равно работе по преодолению силы трения в опорах 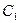и 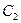, т. е.

,

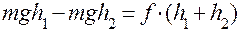отсюда

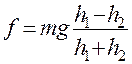(11)

Подставляя в формулу (8) значения V, 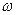и 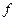из (9), (10) и (11) получим окончательное выражение для вычисления момента инерции махового колеса:

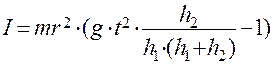(12)