Экспериментальная установка

Теория метода

Отношение теплоемкостей газа при постоянном давлении и при постоянном объеме 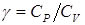играет в термодинамике весьма важную роль. В частности, оно входит в уравнение Пуассона, которое описывает адиабатическое расширение газа (процесс, который протекает без обмена теплом между термодинамической системой и окружающей средой)

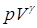=const. (1)

Поскольку идеальной теплоизоляции не существует, то реальный процесс не может быть строго адиабатическим. Но если термодинамический процесс проходит быстро, то за время протекания процесса сколько-нибудь значительный теплообмен произойти не успевает, и такой процесс можно с достаточной точностью считать адиабатическим. Этот прием используется в одном из самых простых методов определения 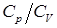– методе адиабатического расширения и изохорического нагрева (метод Клемана и Дезорма).

Пусть в закрытом стеклянном сосуде находитсяисследуемый газ при комнатной температуре Т₁ и давленииp₁,несколько превышающем атмосферное давление p₀.

Откроем кран, сообщающий сосуд с атмосферой. Давление газа начнет сравниваться с атмосферным, а его температура сначала несколько понизится из-за быстрого расширения, а затем снова начнет приближаться к комнатной.

Если теплопроводность стенок сосуда мала (стекло обладает, как известно, низкой теплопроводностью), а отверстие крана достаточно велико, то равновесие по давлению устанавливается значительно быстрее, чем равновесие по температуре, т.е.

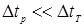, (2)

где через 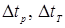обозначены соответственно времена выравнивания давления и температуры.

Пусть кран был открыт в течение промежутка времени 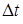такого, что

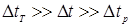. (3)

В этом случае теплообменом, происходящимза время 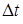через стенки баллона, можно пренебречь, и процесс расширения оказывается почти адиабатическим.

Заметим, что в конце адиабатического расширения давление р₂ равно атмосферному давлению р₀, а температура Т₂ оказывается несколько ниже комнатной температуры Т₁, т. е. Т₂ <Т₁ (температура газа понижается, так как работа расширения совершается за счет внутренней энергии газа)[1].

Переходя в (1) с помощью уравнения Менделеева – Клапейрона к переменным р, Т, найдем, что для адиабатического процесса

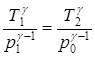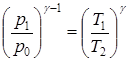или . (4)

После того, как кран вновь отключает сосуд от атмосферы, происходит медленное изохорное нагревание газа со скоростью, определяемой теплопроводностью стеклянных стенок. Вместе с ростом температуры растет и давление газа. За время

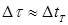
система достигает равновесия, и установившаясятемпература газаT становится равной комнатной температуре T₁.

Процесс выравнивания температуры при закрытомкранеподчиняется закону Гей-Люссака (изохора)

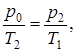откуда 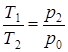. (5)

Исключая с помощью (5) отношение температур T₁/Т₂ из (4), найдем

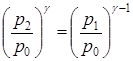или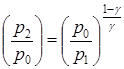

Разрешим это уравнение относительно 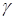. Для этого прологарифмируем это равенство. Получим

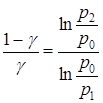, откуда 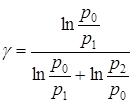. (6)

Таким образом, определение показате­ля адиабаты по методу Клемана-Дезорма требует последовательного проведения с исследуемым газом двух термодинамиче­ских процессов – адиабатического (1-0) и изохорного (0-2) (см. рис.1). Показатель адиабаты определяется тремя давлениями – p₁ и p₀ до и после адиабатического рас­ширения и давлением p₂ после изохорно­го нагревания системы до первоначальной температуры. При этом измерений температуры не требуется.

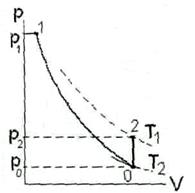
Рис. 1. Метод Клемана-Дезорма: последовательность термодинамических процессов

Экспериментальная установка

Экспериментальная установка (рис.2) состоит из стеклянного баллона А, снабженного краном К, и U – образного манометра М, измеряющего избыточное, по сравнению с атмосферным, давление газа в баллонеА. U– образный манометр заполнен водой.

Измерения 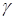проводятся для воздуха. При измерении 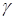для воздуха избыточное давление в баллоне А создается с помощью резиновой груши Г, подсоединенной к баллону трубкой Д, снабженной краном К₁.

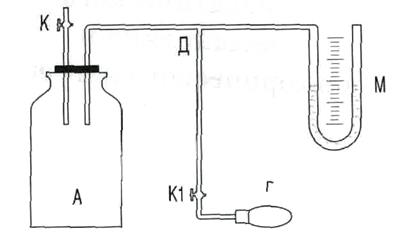
Рис. 2. Установка для определения 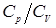методом Клемана и Дезорма

Теория эксперимента

В нашем эксперименте давления р₁ и р₂ мало отличаются от p₀ и формулу (6) можно существенно упростить. Введем обозначения

, (7)

где р₀ – атмосферное давление, а Δ р₁ и Δ р₂ – избыточные давления, которые измеряются водяным манометром М.

Избыточные давления, измеряемые U – образным манометром, пропорциональны разности уровней воды в коленах манометра 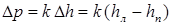, где h_л – уровень воды в левом, а h_п – в правом колене манометра, k – коэффициент пропорциональности (в Па/см). Поэтому равенства (7) можно переписать в виде

, (8)

где 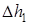– показания манометра до адиабатического расширения, а 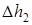– показания манометра после изохорного нагревания газа до комнатной температуры.

Подставляя равенства (8) в уравнение (6), и преобразовывая его, получим

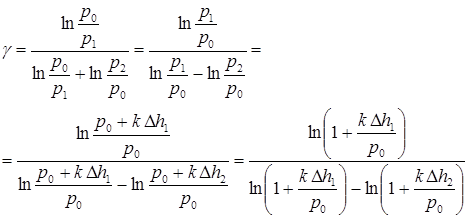(9)

Разлагая выражения с логарифмами в последнем равенстве в ряд по малому параметру 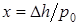[2] и пренебрегая членами второго порядка малости, получим

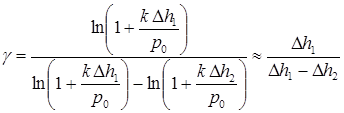. (10)

При желании можно вычислить следующий член ряда и оценить, таким образом, величину ошибки, возникающую при использовании формулы (10).

Как следует из (10), для определения 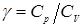необходимо знать избыточное (над атмосферным) давление в баллонедоадиабатического расширения газа и его избыточное давление после изохорного нагревания.

Следует подчеркнуть, что обе величины должны измеряться в состоянии термодинамического равновесия, т. е. после прекращения теплообмена.

При выводе формулы (6) предполагалось, что в момент, когда кран закрывается, давление в сосуде равно атмосферному. Это не совсем точно, так как истечение воздуха сопровождается колебаниями давления, и в момент отключения от атмосферы давление в сосуде может быть как больше, так и меньше атмосферного. Это приводит к тому, что при малых временах 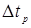(меньше 1с) результаты отдельных измерений заметно отличаются друг от друга (случайный разброс). При увеличении времени 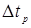(больше 1с) колебания давления становятся меньше, но за это время происходит заметный теплообмен. Следствием является уменьшение давления 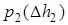и занижение значения 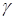. Поэтому окончательный результат мы будем получать экстраполяцией зависимости 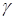от 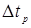к значению 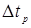= 0.

Выполнение работы

1. Перед началом работы убедитесь, что краны и места сочленений трубок достаточно герметичны. Для этого наполните баллон с помощью резиновой груши воздухом до давления, превышающего атмосферное на 10-25 см вод. ст., и перекройте кран K₁.

Увеличение давления в баллоне сопровождается повышением температуры. Вследствие теплопроводности стенок с течением времени происходит понижение температуры воздуха в баллоне и вместе с тем понижение давления (изохорное охлаждение).

По U-образному манометру проследите за тем, как изменяется давление Δh₁ (разность уровней воды в левом и правом коленах: Δh₁=h_л-h_п) в баллоне с течением времени t. Результаты измерений запишите в табл.1.

Таблица 1

t, с

…

hл, см

hп, см

Δh1, см

Если установка достаточно герметична, то по истечении некоторого времени 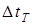, необходимого для установления термодинамического равновесия, давление в баллоне перестанет понижаться. В противном случае необходимо найти и устранитьтечь.

2. Постройте график Δh₁=f(t).

Из графика определите время установления термодинамического равновесия 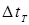. Все последующие измерения следует проводить после установления равновесных условий в установке.

После проведения предварительного опыта приступите к основному эксперименту.

Таблица 2

№ измерения	Давление Δр1	Давление Δр2		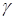	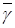Δ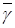
hл, см	hп, см	Δh1, см	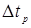, с	hл, см	hп, см	Δh2, см
				0,5

3. Снова наполните баллон с помощью резиновой груши воздухом до давления превышающего атмосферное на 10-25 см вод. ст. и перекройте кран K₁. Выждите время 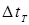и после установления термодинамического равновесия занесите в таблицу 2 значения уровня жидкости в левом (h_л) и в правом (h_п) коленах манометра (колонки 2 и 3 таблицы).Рассчитайте и занесите в таблицу избыточное давление воздуха в баллоне Δh₁ = h_л – h_п (колонка 4).

Затем на очень короткое время ( 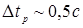) откройте кран К и снова его закройте. Температура газа сравняется с комнатной через время ~ 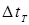. Поэтому выждите некоторое время и после установления термодинамического равновесия снова зафиксируйте по U-образному манометру уровень жидкости в левом и правом коленах (колонки 6 и 7 табл. 2). Рассчитайте и запишите в таблицу избыточное давление воздуха в баллоне Δh₂ = h_л – h_п (колонка 8).

4. Пункт 3 повторите еще 9 раз при .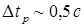

5. Проведите по 3 измерения h_л, h_п,Δh₁ и h_л, h_п,Δh₂ для значений времени 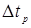3, 5, 8 и 10 с. Время открытого крана контролируйте с помощью секундомера, включая его одновременно с открытием крана К. Результаты запишите в табл.2.

6. После окончания работы обязательно откройте кран К во избежание выдавливания воды из манометра в результате колебаний атмосферного давления.

7. По полученным данным с помощью (10) вычислите и запишите в табл. 2 (колонка 9) значения показателя адиабаты .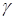

8. Найдите 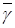и 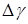(методом среднего квадратичного) для каждого времени 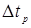(колонки 10 и 11, табл. 2). Постройте график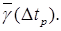

9. Окончательный результат получается экстраполяцией зависимости 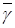от 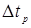к значению 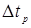= 0. Оцените (графически) ошибку окончательного значения 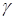. Сделайте выводы по работе.

Контрольные вопросы

1. Какой процесс называется адиабатическим? Какая зависимость отражает этот процесс? Как его можно осуществить?

2. Почему при наполнении баллона воздух в нем нагревается?

3. Какая из теплоемкостей С_p или C_V больше? Почему? Как связаны между собой удельные и молярные теплоемкости при постоянном давлении и постоянном объеме?

4. Каков физический смысл показателя адиабаты? Чему равна величина отношения С_p/C_V для разных газов и для воздуха?

5. Опишите последовательность процессов, имеющих место в сосуде на разных этапах выполнения данной работы.

6. Какой процесс называется изохорным? Как связаны давление и температура в изохорном процессе?

7. Почему после того, как перекрывается связь баллона с атмосферой, давление в нем растет?

8. Охарактеризуйте метод Клемана-Дезорма, применяемый в работе для определения показателя адиабаты.

9. Каковы источники ошибок в данной работе?

[1] Исследование адиабатического расширения газа удобно производить в переменных р, Т, а не р, V, потому что процесс происходит при переменной массе газа, остающегося в баллоне. Изменение массы газа никак не сказывается на вычислениях в переменных р, Т, но крайне неудобно при использовании в качестве независимой переменной объема, занимаемого газом.

[2]