Количество информации и энтропия

Информация - это сведения, относительно которых перед их получением имеется некоторая неопределенность. Потому что, если неопределен­ность отсутствует, то отсутствует и информация.

Пример 1. Из Москвы в Краснодар в 23.00 передается со­общение о том, что в данный момент в Москве ночь. Это сообщение не несет информации (ее количество равно 0) , так как вероятность этого события равна 1 (неопределенность отсутствует).

Пример 2. Второе сообщение: 25 июня в Москве t > + 20⁰ С. Здесь передается какое-то количество информации, так как неопределенность была (могло быть и меньше +20⁰ ) .

Пример 3. Сообщение: 25 июня в Москве выпал снег.

Интуитивно мы чувствуем, что информации в этом сообщении больше, чем в предыдущем.

Таким образом, установлено, что количество информации определяется неопределенностью и связано с вероятностями появления событий. Такая связь выражается формулой

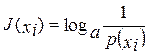, (2.1)

где I (x_i) - количество информации о событии,

P (x_i) - вероятность появления событий.

Для 1 примера 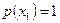и .

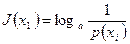Для 3 примера p(x₃)<p(x₂) второго примера и, следовательно,

.

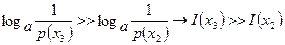Следовательно, 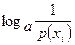одновременно характеризует неопределенность данного события X_i и при его реализации определяет количество информации о данном событии.

Таким образом (2.1), может быть использовано для определения энтропии события

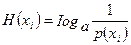. (2.2)

Величины I(x_i) и Н (x_i) , характеризующие отдельное событие X_i , принято называть частным количеством информации и частной энтропией.

Количество информации и неопределенность для всей совокупности событий можно получить путем усреднения

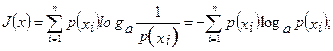(2.3) 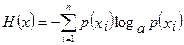. (2.4 )

Выражения (2.3) и (2.4) определяют средние значения количества информации и энтропии.

Несмотря на совпадение (2.3) и (2.4) энтропия Н(Х) и количество информации I(x) принципиально различны. Н(х) объективно характеризует совокупность событий /источник сообщений/ и может быть вычислена априорно. I(х) определяется апостериорно, т.е. после получения сообщения.

Совпадение выражений (2.3) и (2.4) свидетельствует лишь о том, что количество получаемой информации численно равно энтропии, которая имела место относительно источника сообщений.

Единицы измерения I(x) и H(x) зависят от выбора основания логарифма в (2.3) и (2.4) . При использовании десятичных логарифмов I(x) и H(x) определяются в десятичных единицах - дитах.

В случае использования двоичных логарифмов - в двоичных единицах-битах. И при использовании натуральных логарифмов - в нитах. Наиболее употребительные - биты.

Мера количества информации в виде (2.3) впервые была предложена К. Шенноном в 1948 г. и затем более строго определена А.Я. Хинчиным.

Свойства энтропии

Дискретный источник

Формула (2.4) выражает энтропию дискретных источников сообщений и обладает следующими свойствами:

а/ энтропия есть величина вещественная, ограниченная и не отрицательная. Это следует из условия ;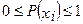

б/ энтропия детерминированных сообщений равна 0.

.

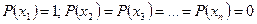В (2.4) первый член равен 0, т.к. 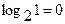. Остальные члены равны 0, так как

.

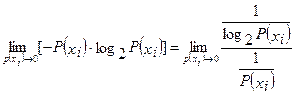Раскрываем неопределенность по правилу Лопиталя

.

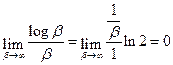в/ энтропия максимальна, если все события равновероятны

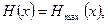если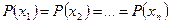

Это понятно индуктивно, и строго доказывается путем нахождения условного экстремума H(x) методом неопределенных множителей Лагранжа.

.

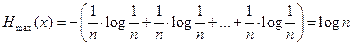Для двух событий H_max(x) =log ₂2=1дв. ед.

Непрерывный источник

Непрерывное сообщение характеризуется плотностью распределения вероятностей f(x) и вероятность события Х_i определяется выражением

.

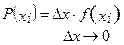Тогда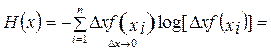

.

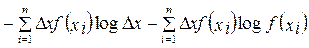Переходя к пределу, получаем

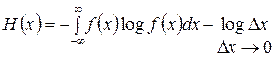, (2.6)

так как .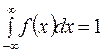

Таким образом, энтропия Н(х) непрерывных сообщений
стремится к бесконечности при 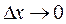. Однако в реальных условиях 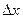имеет конечную величину в виду конечной точности и разрешающей способности аппаратуры.

Поэтому выражение (2.6) имеет две составляющие.

Первая составляющая

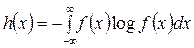(2.7)

называется дифференциальной энтропией непрерывного сообщения.

Вторая составляющая является постоянной величиной, не зависит от статистики сообщения и поэтому исключается из рассмотрения.

Окончательно для определения энтропии непрерывного сообщения запишем

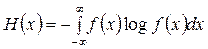. (2.8)