Описание лабораторного макета

Лабораторная работа выполняется на компьютере с использованием виртуального макета. Структурная схема макета приведена на рис. 2. В состав лабораторного макета входят: источник дискретных сообщений, генератор случайных частот появлений знаков и кодеры Хаффмана и Шеннона-Фано. Объем алфавита источника M_A устанавливается в пределах от 2 до 16. Переключатель позволяет устанавливать частоты появлений знаков вручную или от генератора случайных значений. Кодер работает пошагово, результаты его работы отображаются на дисплее.

Рисунок 2 – Структурная схема лабораторного макета

Требования к отчету

7.1 Название лабораторной работы.

7.2 Цель работы.

7.3 Результаты выполнения домашнего задания.

7.4 Структурные схемы исследований и результаты выполнения пп. 5.2...5.4 лабораторного задания (построение дерева кодирования Хаффмана и таблицы Шеннона-Фано, расчеты средней длины кодовых комбинаций, коэффициента эффективности, коэффициента сжатия).

7.5 Выводы по каждому из пунктов задания, в которых представить анализ полученных результатов (совпадение теоретических и экспериментальных данных, результатов домашнего и лабораторного заданий).

7.6 Дата, подпись студента, виза преподавателя с оценкой в 100-балльной шкале.

ЛР 2.2 Исследование алгоритмов эффективного
кодирования с укрупнением алфавита

Цель работы

1.1 Изучение принципа укрупнения алфавита с целью эффективного (экономного) кодирования.

1.2 Исследование эффективности кодирования с укрупнением алфавита для источников дискретных сообщений без памяти и с памятью.

Ключевые положения

2.1 Источник дискретных сообщений – это источник, который выдает последовательность знаков конечного алфавита объемом M_A. Дискретные источники классифицируются на:

– источники без памяти – появление любого знака последовательности не зависит от предыдущих знаков. Такой источник задается безусловными вероятностями знаков алфавита P(a_k), для k = 1, 2,…, M_A...

– источники с памятью – появление любого знака последовательности зависит от предыдущих знаков. Такой источник задается условными вероятностями знаков алфавита. Для математического описания источников дискретных сообщений с памятью используют цепи Маркова, а такие источники называются марковскими K-го порядка. В этом случае появление любого знака последовательности зависит только от K предыдущих знаков. Тогда марковский источник 1-го порядка (когда вероятность появления знака в последовательности зависит только от предыдущего знака) будет задаваться условными вероятностями P(a_k /a_j), для k, j = 1, 2,…, M_A...

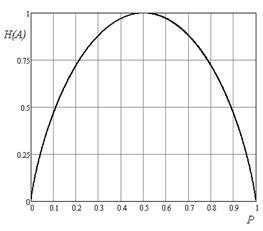
2.2 Двоичный источник сообщений (M_A = 2) без памяти задается безусловными вероятностями P(a₁) = p и P(a₂) = (1 – p). Зависимость энтропии такого источника от p показана на рис. 1 и записывается как:

H(A) = –plog₂p – (1 – p)log₂(1 – p). (1)

H(A), дв.ед.

Энтропия максимальная, когда знаки равновероятные (P(a₁) = P(a₂) = 0,5) и равна 1 дв. ед. Таким образом, каждый символ в среднем содержит не больше 1 дв. ед. информации. В случае, когда p ¹ 0,5 – энтропия H(A) < H_max(A) и такой источник имеет избыточность. При p = 0 или p = 1 энтропия равна 0, поскольку неопределенность отсутствует.

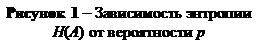
2.3 Для марковского двоичного источника сообщений с памятью 1-го порядка необходимо задать условные вероятности P(a₁/a₁), P(a₁/a₂), P(a₂/a₁) и P(a₂/a₂). Энтропия такого источника определяется:

H(A) = – 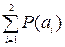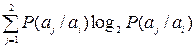. (2)

Пример 1. Задан марковский двоичный источник сообщений с памятью 1‑го порядка с вероятностями P(a₁) = P(a₂) = 0,5; P(a₁/a₁) = P(a₂/a₂) = 0,3; P(a₁/a₂) = P(a₂/a₁) = 0,7. Найти энтропию источника.

По формуле (2) находим

H(A) = – 0,5(0,3log₂0,3 + 0,7log₂0,7) – 0,5(0,3log₂0,3 + 0,7log₂0,7) = 0,881 дв.ед.

Энтропия источника с памятью меньше, чем энтропия источника без памяти с равными вероятностями (H_max(A) = 1 дв.ед.). В этом случае избыточность обусловлена статистической связью между знаками.

2.4 В случае двоичного источника без памяти, когда знаки разновероятные, энтропия меньше 1 дв.ед. (рис. 1). Например, P(a₁) = 0,8 , P(a₂) = 0,2. Тогда энтропия равна H(A) = 0,722 дв.ед. Применение эффективного кодирования (например, кода Хаффмана) к такому двоичному источнику не даст никакого эффекта (каждый из знаков будет кодироваться одним двоичным символом, независимо от вероятности его появления). Для эффективного кодирования нужное предварительное укрупнение алфавита.

Под укрупнением алфавита будем понимать формирование нового алфавита укрупненных знаков (укрупненный знак является соединением из m знаков первичного алфавита). Объем нового (вторичного) алфавита M_B определяется как

M_B = 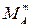. (3)

Кодирование укрупненного (вторичного) алфавита будет более эффективным.

Пример 2. Рассмотрим укрупнение по 3 знака (m = 3) для двоичного приведенного выше источника без памяти с энтропией H(A) = 0,722 дв.ед.

Поскольку двоичный источник без памяти (т.е. такой, что выдает знаки независимо друг от друга), то вероятность появления укрупненного знака будет равна произведению вероятностей входящих у него знаков первичного алфавита (P(a₁a₁) = P(a₁)P(a₁)). Объем укрупненного алфавита по формуле (3) равен M_B = 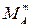= 2³ = 8. Рассчитаем вероятности укрупненных знаков и применим к ним эффективное кодирование (например, кодом Шеннона-Фано) (табл. 1).

Таблица 1 – Кодирование укрупненного алфавита

Укрупненные знаки bi	Вероятности P(bi)	Подгруппы	Кодовые комбинации
I	II	III	IV	V
a1a1a1	0,512
a1a1a2	0,128
a1a2a1	0,128
a2a1a1	0,128
a1a2a2	0,032
a2a1a2	0,032
a2a2a1	0,032
a2a2a2	0,008

Средняя длина кодовых комбинаций для укрупненных знаков:

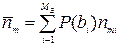= 2,184 символов,

а среднее число кодовых символов на знак определяется как

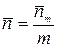. (4)

Для рассмотренного случая получим = 0,728 символов. Из сравнения с энтропией H(A) = 0,722 дв.ед. видно, что предварительное укрупнение алфавита значительно повысило эффективность сжатия (кодирование первичного алфавита без укрупнения давало = 1).

С увеличением количества знаков при укрупнении m можно получать более эффективный код, т.е. среднее число кодовых символов на знак будет больше приближаться к энтропии.

2.5 Укрупнение алфавита также целесообразно в случае источника дискретных сообщений с памятью. Известно, что статистическая зависимость между знаками первичного алфавита, расположенных рядом, больше, чем расположенных на расстоянии нескольких знаков. Соответственно, укрупненные знаки будут иметь значительно меньшую зависимость (очевидно, что чем больше m, тем меньше зависимость между укрупненными знаками). В этом случае (для источника с памятью) для определения вероятностей укрупненных знаков необходимо учитывать условные вероятности (P(a_ka_j) = P(a_k)P(a /a_k)).

Таким образом, избыточность, обусловленная статистическими связями между знаками первичного алфавита, превратится в избыточность, обусловленную разными вероятностями укрупненных знаков. А такую избыточность можно уменьшить, используя эффективное кодирование (например, код Хаффмана).

Ключевые вопросы

3.1 Дать определение дискретного источника без памяти.

3.2 Дать определение дискретного источника с памятью.

3.3 Объяснить принцип укрупнения алфавита.

3.4 С какой целью применяют укрупнение алфавита?

3.5 Как определяются вероятности укрупненных знаков для источников без памяти и с памятью?

3.6 Как определяется объем укрупненного алфавита?

3.7 Как влияет на эффективность кодирования количество знаков при укрупнении m? Чем обусловливается выбор m?

3.8 Каким образом эффективное кодирование укрупненного алфавита позволяет уменьшить избыточность сообщений при кодировании источников дискретных сообщений с памятью?

Домашнее задание

4.1. Изучить раздел “Эффективное кодирование источников дискретных сообщений” по конспекту лекций и ключевым положениям. Также можно воспользоваться литературой [2, с. 16...27; 5, с. 876...887]. Изучить описание лабораторного макета в разд. 6.

4.2 Задан двоичный источник сообщений без памяти с алфавитом {a₁; a₂} с вероятностями P(a₁) = (0,8 – 0,02N), где N – номер Вашей бригады. Рассчитать энтропию источника. Провести укрупнение алфавита по двум знакам. Составить кодовые комбинации для укрупненного алфавита методом Шеннона-Фано (для нечетных N) и методом Хаффмана (для четных N). Рассчитать 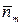, , ηи m.

4.3 Подготовиться к обсуждению по ключевым вопросам.

Лабораторная задача

5.1 Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 2.2 Исследование алгоритмов эффективного кодирования с укрупнением алфавита, используя иконку Лабораторные работы на рабочем столе, а затем папки ТЭС и Модуль 2. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.2 Исследовать эффективность укрупнения алфавита при кодировании двоичного источника без памяти с равными вероятностями знаков. Выбрать в меню двоичного источника сообщений – “без памяти (равновероятные)”. Записать характеристики первичного сообщения.

Установить укрупнение алфавита по двум знакам. Зафиксировать в протоколе знаки укрупненного алфавита, соответствующие им вероятности и кодовые комбинации. Записать значения энтропии укрупненного сообщения H(A), 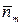и . Сравнить энтропию первичного сообщения и после укрупнения. Рассчитать эффективность кодирования и коэффициент сжатия. Коэффициент сжатия можно рассчитать

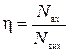, (5)

где N_вх – количество двоичных символов (знаков), использованных для передачи сообщения до кодирования;

N_вих – количество двоичных символов (знаков), использованных для передачи сообщения после кодирования.

Повторить п. 5.2 при укрупнении алфавита по трем и четырем знакам.

5.3 Исследовать эффективность укрупнения алфавита при кодировании двоичного источника без памяти с разными вероятностями знаков. Выбрать в меню двоичного источника сообщений – “без памяти (разновероятные)”.

Повторить исследование, проведенные в п. 5.2, для двоичного источника без памяти с разными вероятностями знаков.

5.4 Исследовать эффективность укрупнения алфавита при кодировании марківського двоичного источника с памятью 1-го порядка. Выбрать в меню двоичного источника сообщений - “С памятью 1-го порядка”.

Повторить исследования, проведенные в пп. 5.2 и 5.3, для марковского двоичного источника с памятью 1-го порядка.