Iii. структура та храрактеристика завдань вступного випробування
Для перевірки теоретичної і практичної підготовки вступників екзамен проводиться у формі тесту, складеного відповідно до цієї програми. На виконання тесту відведено 180 хвилин (3 години).
Тест складається з двох частин:
1. Частина А складається з 70 тестовихпитань. Це завдання з вибором однієї правильної відповіді. Завдання формулюється у формі питання (задачі) з кількома (4-7) варіантами відповідей на нього (закрита форма тестового завдання). Серед відповідей правильною є лише одна. Виконуючи завдання, необхідно вказати правильний варіант відповіді.
2. Частина Б включає 3 практичних завдання (задачі). Виконуючи завдання, необхідно відтворити і записати повний хід розв’язання.
IV. КРИТЕРІЇ ОЦІНЮВАННЯ
1. Правильна відповідь на питання частини А оцінюється в 1 бал, а неправильна – 0 балів [всього максимум за частину А – 70 балів].
2. Розв’язання практичних завдань частини Б оцінюється за диференційованою шкалою [всього максимум за частину Б – 30 балів]: за кожну із трьох задач частини Б від 0 до 10 балів. Задачі вибираються випадково – одна із номерів 1-10, друга із номерів 11-20, третя із номерів 21-30.
3. Розподіл балів:
a. 0 балів – завдання не розв’язане;
b. 2 бали - приведені деякі правильні формули, які мають відношення до задачі;
c. 4 бали – запропонована правильна ідея розв’язання, але допущені помилки призвели до значного спотворення відповіді (висновків);
d. 6 бали – запропонована правильна ідея розв’язання, але допущені помилки призвели до незначного спотворення відповіді (висновків); або не подано (подано на недостатньому рівні) обґрунтування вибору способу розв’язання;
e. 8 балів – завдання розв’язане, подано обґрунтування способу розв’язання, але допущені помилки технічного характеру;
f. 10 балів – завдання розв’язане повністю (з обґрунтуванням способу розв’язання).
Загальна максимальна сума балів: 100 балів.
Як працювати над тестом
Навіть якщо ви впевненні у правильності відповіді, уважно прочитайте всі варіанти, щоб остаточно переконатися у правильності свого вибору, якщо вам здаються правильними два варіанти відповіді, то вибирайте найбільш повний. Для відповіді на деякі питання потрібно буде виконати математичні перетворення (для чернетки використовуйте поля)
Необхідно ретельно та охайно заповнити бланк відповідей для частини А, виданий разом із тестовими завданнями.
| Х |
Правильну відповідь необхідно позначити у бланку
Розв’язок задач частини Б записуєте безпосередньо під умовами.
Частина А.
- Кристали можуть мати осі поворотної симетрії наступних порядків
| А) 1,2,3,4,5,6 | В) 1,2,3,4,6 |
| Б) 2,3,4,5,6 | Г) 2,3,4,6,7 |
- Решіток Браве існує
| А) 7 | В) 15 |
| Б) 14 | Г) 230 |
- На один вузол ОЦК- гратки з періодом гратки а припадає об’єм
А) 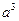 | В) 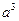 /4 /4 |
Б) 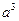 /2 /2 | Г) 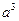 /6 /6 |
- На один вузол ГЦК- гратки з періодом гратки а припадає об’єм
А) 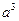 | В) 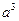 /4 /4 |
Б) 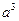 /2 /2 | Г) 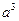 /6 /6 |
- Найбільшу міжплощинну відстань у простій кубічній гратці мають площини сімейства
| А) (1 0 0) | В) (1 1 1) |
| Б) (1 1 0) | Г) (3 1 1) |
- Найбільшу міжплощинну відстань у ОЦК- гратці мають площини сімейства
| А) (1 0 0) | В) (1 1 1) |
| Б) (1 1 0) | Г) (3 1 1) |
- Найбільшу міжплощинну відстань у ГЦК- гратці мають площини сімейства
| А) (1 0 0) | В) (1 1 1) |
| Б) (1 1 0) | Г) (3 1 1) |
- Кількість найближчих сусідів у вузла простої кубічної гратки рівна
| А) 6 | В) 12 |
| Б) 8 | Г) 4 |
- Кількість найближчих сусідів у вузла ОЦК- гратки рівна
| А) 6 | В) 12 |
| Б) 8 | Г) 4 |
- Кількість найближчих сусідів у вузла ГЦК- гратки рівна
| А) 6 | В) 12 |
| Б) 8 | Г) 4 |
- Кількість найближчих сусідів у вузла гексагональної щільнопакованої гратки
рівна
| А) 6 | В) 12 |
| Б) 8 | Г) 4 |
- Кількість найближчих сусідів у вузла алмазної гратки рівна
| А) 6 | В) 12 |
| Б) 8 | Г) 4 |
- Параметр гратки, оберненої до простої кубічної з параметром а, рівний
А) 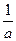 | В) 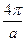 |
Б) 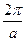 | Г) 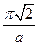 |
- Параметр гратки, оберненої до ОЦК-гратки, рівний
А) 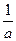 | В) 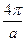 |
Б) 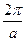 | Г) 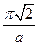 |
- Параметр гратки, оберненої до ГЦК-гратки, рівний
А) 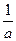 | В) 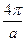 |
Б) 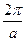 | Г) 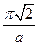 |
- Зв’язок між параметром гратки, міжплощинною відстанню і індексами Міллера
А) 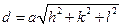 | В) 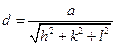 |
Б) 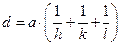 | Г) 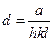 |
- Проста кубічна гратка має параметр гратки а. Які довжини хвилі можуть дати дифракційну картину від такої гратки?
А) 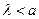 | В) 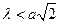 |
Б) 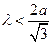 | Г) 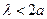 |
- ОЦК- гратка має параметр гратки а. Які довжини хвилі можуть дати дифракційну картину від такої гратки?
А) 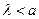 | В) 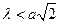 |
Б) 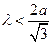 | Г) 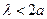 |
- ГЦК- гратка має параметр гратки а. Які довжини хвилі можуть дати дифракційну картину від такої гратки?
А) 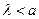 | В) 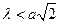 |
Б) 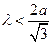 | Г) 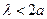 |
- Базисні вектори ГЦК гратки:
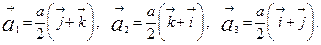 Базисний вектор
Базисний вектор 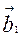 оберненої гратки
оберненої гратки
А) 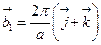 | В) 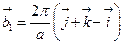 |
Б) 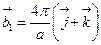 | Г) 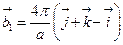 |
- Базисні вектори ОЦК гратки:
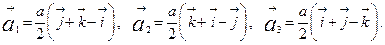 Базисний вектор
Базисний вектор 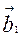 оберненої гратки
оберненої гратки
А) 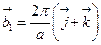 | В) 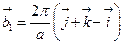 |
Б) 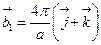 | Г) 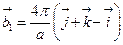 |
- Імовірність електрону рухатись без зіткнень протягом часу t рівна
А) 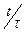 | В) 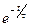 |
Б) 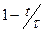 | Г) 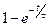 |
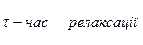 |
- Середній квадрат часу до зіткнення
А) 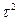 | В) 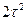 |
Б) 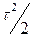 | Г) 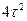 |
- Середній куб часу до зіткнення
А) 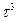 | В) 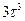 |
Б) 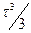 | Г) 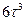 |
- Питомий опір провідника
А) 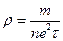 | В) 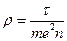 |
Б) 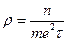 | Г) 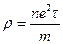 |
- Електричне поле в металі включили в момент t=0. Густина струму змінюється з часом за законом:
А) 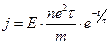 | В) 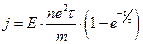 |
Б) 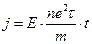 | Г) 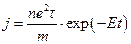 |
- Формула для ефекту Холла:
А) 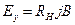 | В) 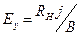 |
Б) 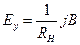 | Г) 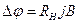 |
- Закон Відемана-Франца для теплопровідності
А) 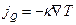 | В) 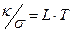 |
Б) 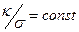 | Г) 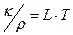 |
А) 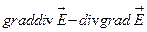 | В) 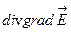 |
Б) 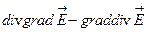 | Г) 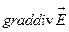 |
- На кожну комірку оберненого простору об’ємом
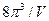 припадає два квантових стани вільних електронів із протилежними спінами. Знайти звідси енергію Фермі.
припадає два квантових стани вільних електронів із протилежними спінами. Знайти звідси енергію Фермі.
А) 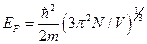 | В) 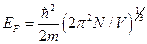 |
Б) 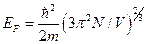 | Г) 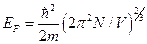 |
- Середня енергія вільних електронів при
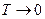
А) 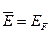 | В) 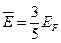 |
Б) 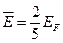 | Г) 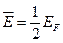 |
- Температура Фермі металів має порядок
А) 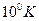 | В) 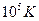 |
Б) 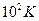 | Г) 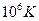 |
- Довжина хвилі де Бройля (за порядком величини), що відповідає енергії Фермі
А) 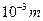 | В) 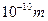 |
Б) 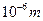 | Г) 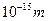 |
- Розподіл Фермі-Дірака
А) 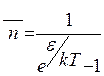 | В) 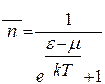 |
Б) 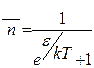 | Г) 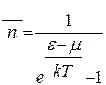 |
- Молярна теплоємність електронного газу
А) 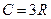 | В) 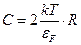 |
Б) 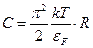 | Г) 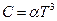 |
- Середня енергія квантового гармонічного осцилятора частотою
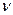
А) 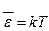 | В) 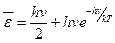 |
Б) 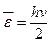 | Г) 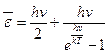 |
- Дозволені значення енергії квантового гармонічного осцилятора частотою
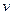
А) 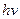 | В) 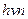 |
Б) 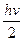 | Г) 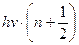 |
- Закон дисперсії
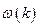 для одноатомного ланцюжка з константою пружності
для одноатомного ланцюжка з константою пружності 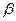 :
:
А) 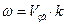 | В) 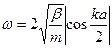 |
Б) 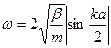 | Г) 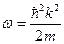 |
- Теплоємність діелектрика при низьких температурах
А) 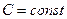 | В) 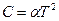 |
Б) 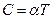 | Г) 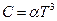 Д) Д) 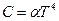 |
- Теплоємність двовимірного діелектрика при низьких температурах
А) 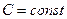 | В) 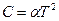 |
Б) 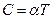 | Г) 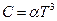 Д) Д) 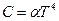 |
- Потенціал Ленарда-Джонса
А) 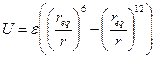 | В) 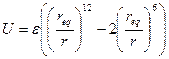 |
Б) 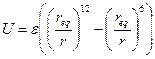 (де (де 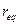 - рівноважна відстань) - рівноважна відстань) | Г) 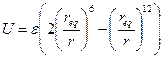 |
- Перша поправка до енергії в стаціонарній теорії збурень (невироджений випадок)
А) 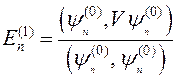 | В) 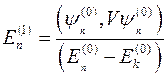 |
Б) 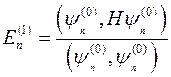 | Г) 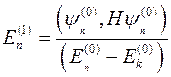 |
- Співвідношення Бора-Гейзенберга
А) 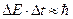 | В) 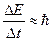 |
Б) 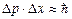 | Г) 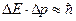 |
- Проникність бар’єру висотою
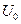 і товщиною
і товщиною 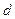 для частинки масою
для частинки масою 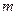 і енергією Е
і енергією Е
А) 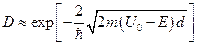 | В) 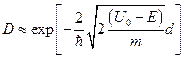 |
Б) 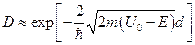 | Г) 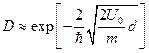 |
- Провідність власних напівпровідників з шириною забороненої зони
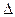 залежить від температури як
залежить від температури як
А) 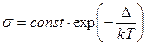 | В) 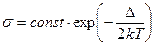 |
Б) 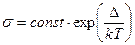 | Г) 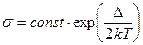 |
- Який із 4-х матеріалів не є напівпровідником
| А)Si | В)GaAs |
| Б)Ge | Г)Bi |
- Який із перелічених матеріалів не стає надпровідником при пониженні температури.
| А)Al | В)Ni |
| Б)Nb | Г)Pb |
- Чим визначається частота струму в нестаціонарному ефекті Джозефсона
А) 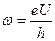 | В) 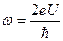 |
Б) 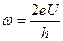 | Г) 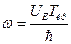 |
- Порядок величини енергії зв’язку куперівської пари в алюмінії
| А)10-19Дж | В) 10-31Дж |
| Б) 10-23Дж | Г) 10-16Дж |
- Квант магнітного потоку
| А) h/e | В) h/(2e) |
| Б) 2h/e | Г) 2e/h |
- Ізотопний ефект критичної температури надпровідника
А) 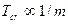 | В) 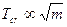 |
Б) 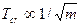 | Г) 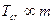 |
- Чому теплопровідність надпровідників знижується із зниженням температури?
| А) фонони повільно рухаються | В) зменшується частка „нормальних електронів” здатних до розсіювання і перенесення енергії |
| Б) неправда-теплопровідність росте із зниженням Т | Г) згідно з законом Відемана-Франца |
- Одиниці вимірювання напруженості магнітного поля
| А) тесла | В) Вольт/метр |
| Б) ампер/метр | Г) гаус |
- Одиниці вимірювання намагніченості
| А) тесла | В) Вольт/метр |
| Б) ампер/метр | Г) гаус |
- Одиниці вимірювання індукції магнітного поля
| А) тесла | В) Вольт/метр |
| Б) ампер/метр | Г) ерстед |
- Характерні значення магнітної сприйнятливості діамагнетиків
| А) 10-6 | В) 10-2 |
| Б) -10-6 | Г) -10-2 |
- Вибрати правильне рівняння:
А) 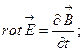 | В) 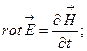 |
Б) 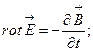 | Г) 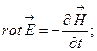 |
- Закон Кюрі для парамагнетиків
А) 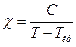 | В) 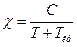 |
Б) 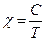 | Г) 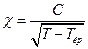 |
- Закон Кюрі-Вейса
А) 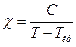 | В) 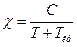 |
Б) 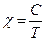 | Г) 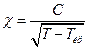 |
- Назвати антиферомагнетик
| А)Fe | В)Ni |
| Б)Cu | Г)Cr |
- Зв’язок між діамагнітною і парамагнітною сприйнятливістю газу вільних електронів
А) 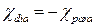 | В) 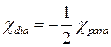 |
Б) 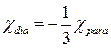 | Г) 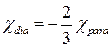 |
- Встановити узагальнені індекси Міллера площин, що дають перші 4 ліній дебаєграми для простої кубічної гратки
| А)1 0 0 1 1 1 2 0 0 3 1 1 | В) 1 1 0 2 0 0 2 1 1 2 2 0 |
| Б)1 0 0 1 1 0 1 1 1 2 0 0 | Г) 1 1 1 2 0 0 2 2 0 3 1 1 |
- Встановити узагальнені індекси Міллера площин, що дають перші 4 ліній дебаєграми для ОЦК-гратки
| А)1 0 0 1 1 1 2 0 0 3 1 1 | В) 1 1 0 2 0 0 2 1 1 2 2 0 |
| Б) 1 0 0 1 1 0 1 1 1 2 0 0 | Г) 1 1 1 2 0 0 2 2 0 3 1 1 |
- Встановити узагальнені індекси Міллера площин, що дають перші 4 ліній дебаєграми для ГЦК-гратки
| А)1 0 0 1 1 1 2 0 0 3 1 1 | В) 1 1 0 2 0 0 2 1 1 2 2 0 |
| Б) 1 0 0 1 1 0 1 1 1 2 0 0 | Г) 1 1 1 2 0 0 2 2 0 3 1 1 |
- Знайти коефіцієнти упаковки (частка об’єму, заповнена атомами-кулями) для ПК. Округлити до цілих процентів.
| А) 50 | Д) 74 |
| Б) 52 | Е) 82 |
| В) 62 | Ж) 100 |
| Г) 68 |
- Знайти коефіцієнти упаковки (частка об’єму, заповнена атомами-кулями) для ОЦК. Округлити до цілих процентів.
| А) 50 | Д) 74 |
| Б) 52 | Е) 82 |
| В) 62 | Ж) 100 |
| Г) 68 |
- Знайти коефіцієнти упаковки (частка об’єму, заповнена атомами-кулями) для ГЦК. Округлити до цілих процентів.
| А) 50 | Д) 74 |
| Б) 52 | Е) 82 |
| В) 62 | Ж) 100 |
| Г) 68 |
- Алгоритм Метрополіса. Зміна стану приймається, якщо:
А) 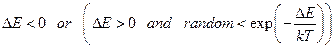 | В) 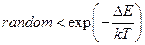 |
Б) 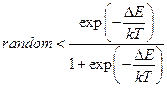 | Г) 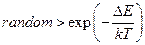 |
- Алгоритм Глаубера. Зміна стану приймається, якщо:
А) 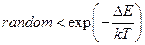 | В) 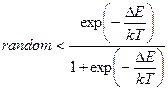 |
Б) 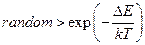 | Г) 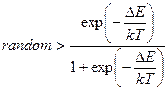 |
- Атом масою
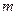 знаходиться в потенціальному полі
знаходиться в потенціальному полі 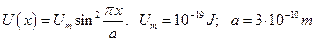 . Знайти період його власних коливань.
. Знайти період його власних коливань.
А) 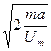 | В) 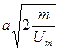 |
Б) 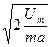 | Г) 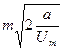 |
Д) 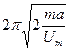 |
Частина Б. Задачі.
Підчастина І
1. Вивести розподіл густини імовірності по часу до наступного зіткнення електрона у металі. Знайти середній час до наступного зіткнення електрона у металі. Знайти середню енергію, що передає електрон металу іонній підсистемі при зіткненні
2. Знайти коефіцієнт теплопровідності електронного газу в рамках класичної електронної теорії. Знайти число Лоренца в законі Відемана-Франца.
3. Знайти вираз для диференціальної термо-е.р.с. для металу в рамках класичної електронної теорії.
4. Розв’язати кінетичне рівняння для імпульсу електрона у гармонійному електричному полі
5. Знайти закон затухання (зростання) струму при вимкненні (увімкненні) електричного поля. Знайти плазмову частоту як частоту вільних коливань електронного газу
6. Знайти фермівський радіус та енергію Фермі у тривимірному та двовимірному кристалах
7. Знайти вираз для функції густини одноелектронних рівнів у металі в рамках квантової моделі вільних електронів. Знайти середнє значення енергії вільних електронів. Знайти тиск газу вільних електронів, які підкоряються статистиці Фермі
8. Знайти коефіцієнт упаковки для ОЦК, ГЦК, ПК і ГЩП граток
9. Довести, що в ГЦК гратці максимальна густина вузлів - у площинах {111}, а
в ОЦК гратці максимальна густина вузлів - у площинах {110}
10. Встановити міллерівські індекси площин, відбивання від яких дає перші 5 ліній дебаєграми для ОЦК гратки, для ГЦК гратки
Підчастина ІІ
11. Знайти теплоємність твердого тіла в рамках моделі Ейнштейна.
12. Довести (використовуючи модель Дебая), що теплоємність твердого тіла при низьких температурах пропорційна кубу температури.
13. Довести (використовуючи модель Дебая), що теплоємність ДВОВИМІРНОГО твердого тіла при низьких температурах пропорційна квадрату температури.
14. Знайти вираз для коефіцієнта теплового розширення, використовуючи модель ангармонійних коливань із кубічним членом у енергії (U=beta/2*x^2-gamma/3*x^3)
15. Знайти нормальні моди коливань лінійної молекули А-В-А (типу СО2) з масами атомів Ма, Мв і жорсткістю пружних зв’язків к.
16. Знайти закон дисперсії пружних хвиль (залежність енергії від хвильового вектора) у одноатомному ланцюжку. Відома маса атомів, середня відстань між атомами і жорсткість пружного зв’язку між сусідніми атомами.
17. Знайти закон дисперсії поблизу границі зони Бріллюена в рамках одновимірної моделі слабкого зв’язку при заданому слабкому періодичному потенціалі V(r).
18. Описати модель сильного зв’язку для ОЦК-гратки.
19. Вивести закон діючих мас для електронів і дірок у власному напівпровіднику.
20. Вивести і проаналізувати вираз для оберненої ефективної маси електрона.
Підчастина ІІІ.
21. Побудувати модель діамагнетика на основі боровської моделі атома. Оцінити діамагнітну сприйнятливість твердого тіла.
22. Побудувати модель парамагнетика, вважаючи спін кожного атома рівним одній другій, а проекцію магнітного момента – плюс-мінус магнетону Бора.
23. Побудувати модель самоузгодженого поля Вейса. Зв’язати параметр Вейса з точкою Кюрі.
24. Побудувати модель Ізінга в наближенні самоузгодженого поля. Виразити температуру фазового переходу спонтанного намагнічування через енергію обмінної взаємодії.
25. Знайти вираз для обмінної взаємодії для випадку двоелектронної системи у вигляді інтегралів.
26. Описати як мінімум 10 властивостей надпровідників.
27. Знайти глибину проникнення магнітного поля в надпровідник у рамках теорії Лондонів.
28. Знайти вираз критичної швидкості для надтекучого гелію через закон дисперсії елементарних збуджень у гелії.
29. Довести властивість квантування магнітного потоку поля надпровідника із струмом на основі теорії Гінзбурга-Ландау.
30. Описати нестаціонарний ефект Джозефсона на основі теорії Гінзбурга-Ландау.
V. РЕКОМЕНДОВАНА ЛІТЕРАТУРА
Основна література.
1. Ч.Киттель. Введение в физику твердого тела. М.1978.
2. А.Ашкрофт, К.Мермин. Физика твердого тела.Т. 1,2. М.1979.
3. Дж.Займан. Принципы теории твердого тела. М. 1974
4. А.Гусак, В.Гриценко, Т.Запорожець. Статистична фізика - основні положення та моделі. Черкаси. 1998.
5. И.Иродов. Задачи по квантовой физике. М.1977.
Додаткова література.
6 .К.Биндер, Д. Хеерман. Моделирование методом Монте-Карло в статистической физике. М.1995.
7 .Д. Хеерман. Методы компьютерного эксперимента в теоретической физике. М.1990.
8 .Ч. Киттель. Квантовая теория твердых тел. М.1967.
9. Ч. Киттель. Статистическая термодинамика. М.1977.
10 .А. Марадудин, З.Монтролл, Дж.Вейсс, Динамика кристаллической решетки в гармоническом приближении. М.1965.
11. Гусак А.М., Богатирьов А.О., Запорожец Т.В. и др. (Под ред. Гусака А.М.) Модели твердофазных реакций. Изд. Черкасского университета, 2004.
12. Gusak A. Diffusion, Reactions, Coarsening – some new ideas. Cherkasy National University Publ., Cherkasy – monograph (in English), 2004
13. Gusak, A.M., and F. Hodaj. “Nucleation in a Concentration Gradient.” Chapter 10 in “Nucleation Theory and Applications”, ed.J.Schmelzer, Wiley VCH (2005): 375-417.
14. А.М.Гусак. Термодинамика необратимых процессов – глава в энциклопедии „Неорганическое материаловедение”, под ред. Г.Г.Гнесина и В.В.Скорохода, Институт проблем материаловедения НАН Украины, с.с. 239-260 (2008)
Голова фахової атестаційної комісії проф., д.ф.-м.н. А.М.Гусак