Задачі для самостійного розв’язування. 13.1. Визначити внутрішню енергію тіла в гармонічному наближенні
13.1. Визначити внутрішню енергію тіла в гармонічному наближенні. Обчислити цю енергію для 1 кг вуглецю при 1200 К та порівняти отриманий результат з теплотою, що виділяється при його згоранні (8093 ккал/кг).
13.2. Знайти середнє значення потенціальної енергії лінійного гармонічного осцилятора, що знаходиться у термостаті, якщо функція Гамільтона для розглядуваного осцилятора має вигляд
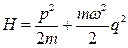 .
.
13.3. Маленький гумовий м’яч скаче вертикально по пружній поверхні. Визначити співвідношення між середньою потенціальною і середньою кінетичною енергією м’яча, розглядаючи його як матеріальну точку.
13.4. За допомогою теореми про віріал показати, що при кеплерівському русі планети по еліпсу її повна енергія від’ємна.
13.5. Знайти розподіл молекул газу за відносними швидкостями 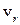 та обчислити
та обчислити 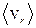 . Визначити також середній кут між швидкостями молекул.
. Визначити також середній кут між швидкостями молекул.
13.6. Знайти число зіткнень однієї молекули з рештою молекул за одиницю часу, вважаючи молекули кулями радіуса 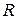 . Визначити також середню довжину
. Визначити також середню довжину 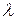 та середній час
та середній час 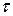 вільного пробігу молекули.
вільного пробігу молекули.
13.7. Молекули полярного газу (наприклад, 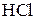 ) є диполями з постійним електричним моментом
) є диполями з постійним електричним моментом 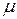 . Газ із невзаємодіючих молекул поміщено в електричне поле напруженістю
. Газ із невзаємодіючих молекул поміщено в електричне поле напруженістю 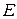 . Визначити розподіл молекул за напрямками та обчислити середнє значення косинуса кута
. Визначити розподіл молекул за напрямками та обчислити середнє значення косинуса кута 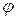 між напрямком поля і диполя.
між напрямком поля і диполя.
13.8. Обчислити енергію Гельмгольца 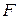 , внутрішню енергію
, внутрішню енергію 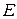 , ізохорну теплоємність
, ізохорну теплоємність 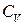 , ентропію
, ентропію 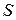 , рівняння стану, енергію Гіббса
, рівняння стану, енергію Гіббса 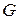 , ентальпію
, ентальпію 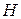 та хімічний потенціал
та хімічний потенціал 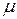 класичного ідеального газу з
класичного ідеального газу з  атомів в об’ємі
атомів в об’ємі 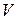 при температурі
при температурі 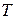 .
.
13.9. Обчислити енергію Гельмгольца 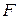 , внутрішню енергію
, внутрішню енергію 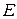 , ізохорну теплоємність
, ізохорну теплоємність 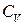 ідеального газу з
ідеального газу з  частинок маси
частинок маси 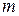 у циліндрі об’єму
у циліндрі об’єму 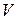 і висотою
і висотою 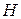 при температурі
при температурі 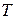 . Циліндр знаходиться в однорідному полі тяжіння.
. Циліндр знаходиться в однорідному полі тяжіння.
13.10. Ідеальний газ з  атомів знаходиться у центрифузі радіуса
атомів знаходиться у центрифузі радіуса 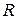 і висотою
і висотою 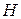 , яка обертається з кутовою швидкістю
, яка обертається з кутовою швидкістю  . Температура газу
. Температура газу 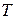 . Обчислити енергію Гельмгольца
. Обчислити енергію Гельмгольца 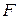 , тиск
, тиск 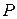 на бокову поверхню центрифуги, внутрішню енергію
на бокову поверхню центрифуги, внутрішню енергію 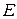 та теплоємність
та теплоємність 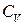 газу.
газу.
Розділ 14
ОСНОВИ КВАНТОВОЇ СТАТИСТИКИ
Теоретичні відомості
Принципи квантової статистики.На рубежі ХІХ і ХХ століть статистична фізика, яка базувалася на механіці Ньютона, почала давати збоїни. Дослідження випромінювання призвело з одного боку до усвідомлення, що останнє є багаточастинковою системою (корпускули-фотони), а з іншого, що його не можна описати з класичних позицій. Крім того, експериментальна досяжність у ті роки досить низьких температур показала, що в цих умовах і традиційні – атомно-молекулярні системи мають властивості, які не пояснюються класичними розподілами. На основі квантових міркувань почала будуватися квантова статистична фізика.
Принциповою особливістю квантової моделі статистичної фізики є те, що сама квантова механіка являє собою статистичну теорію, і статистика, неминуча при вивченні багаточастинкових систем, немов би накладається на статистичність, яка виникає в об’єктах мікросвіту. Іншою особливістю квантової статистики виявляється принципова відсутність поняття фазової траєкторії. Мікростан, який у класичній статистичній фізиці характеризувався точкою у фазовому просторі, через співвідношення невизначеностей розмивається до об’єму ~ h3 (у перерахуванні на одну частинку).
Нагадаємо також, що у квантовій теорії кожній спостережувальній величині А відповідає лінійний ермітів оператор 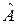 . При цьому середнє значення величини А у стані з хвильовою функцією ψ
. При цьому середнє значення величини А у стані з хвильовою функцією ψ 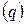 дорівнює
дорівнює
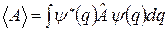 . (14.1)
. (14.1)
Квантовий статистичний ансамбль описується набором станів ψ 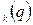 з відповідними ймовірностями
з відповідними ймовірностями 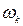 . Тоді середнє значення тієї ж величини А за розподілом
. Тоді середнє значення тієї ж величини А за розподілом 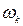 дорівнюватиме
дорівнюватиме
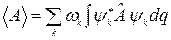 ; (14.2)
; (14.2)
тут k – квантове число. Саме в цій формулі виявляється вищезгадане накладання статистик.
Аналогом фазової щільності у квантовій статистиці стає матриця щільності
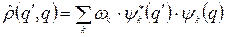 , (14.3)
, (14.3)
а рівнянню Ліувілля відповідає рівняння Неймана
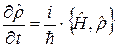 , (14.4)
, (14.4)
де дужками 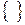 позначається комутатор операторів. Як і у класиці, квантовий рівноважний статистичний ансамбль задовольняє рівнянню
позначається комутатор операторів. Як і у класиці, квантовий рівноважний статистичний ансамбль задовольняє рівнянню
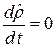 . (14.5)
. (14.5)
Аналогічний до класичного розподілу вигляд має квантовий канонічний розподіл:
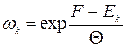 , (14.6)
, (14.6)
де 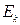 – енергетичний спектр. Умова нормування
– енергетичний спектр. Умова нормування 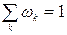 визначає так звану статистичну суму
визначає так звану статистичну суму
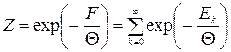 . (14.7)
. (14.7)
Якщо енергетичні рівні виявляються виродженими, враховується фактор 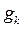 – кратність виродження k-го рівня, тобто кількість квантових станів, що припадають на енергетичний рівень
– кратність виродження k-го рівня, тобто кількість квантових станів, що припадають на енергетичний рівень 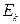 :
:
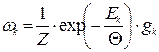 . (14.8)
. (14.8)
При цьому вільна енергія дорівнюватиме
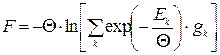 . (14.9)
. (14.9)
В загальному випадку дослідження квантової статистичної системи зводиться до виконання наступної послідовності процедур:
1) знаходиться спектр 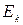 та відповідний набір квантових чисел k;
та відповідний набір квантових чисел k;
2) розраховуються статистична сума Z і вільна енергія F;
3) обчислюються необхідні термодинамічні характеристики системи.
Таку послідовність дій вважатимемо статистичним обґрунтуванням термодинаміки з позицій квантової статистики.
Для систем із змінним числом частинок використовують квантовий великий канонічний розподіл
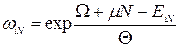 (14.10)
(14.10)
з великою статистичною сумою
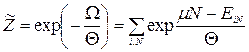 , (14.11)
, (14.11)
де 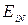 – енергія i-го стану системи з N частинок. Зазначимо, що різним значенням N, як правило, відповідає свій набір квантових чисел i.
– енергія i-го стану системи з N частинок. Зазначимо, що різним значенням N, як правило, відповідає свій набір квантових чисел i.
Квантовий одноатомний ідеальний газ. Розподіли Фермі–Дірака і Бозе–Ейнштейна.Для квантового ідеального одноатомного газу зручно ввести хвильову функцію 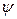 , яка описує стан останнього, як функцію так званих чисел заповнення
, яка описує стан останнього, як функцію так званих чисел заповнення 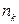 . За визначенням
. За визначенням 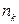 є число частинок газу у k-му індивідуальному для кожної частинки квантовому стані. Отже, хвильова функція
є число частинок газу у k-му індивідуальному для кожної частинки квантовому стані. Отже, хвильова функція 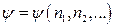 визначатиме багаточастинковий стан, коли у першому індивідуальному стані знаходиться рівно
визначатиме багаточастинковий стан, коли у першому індивідуальному стані знаходиться рівно 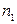 частинок, у другому –
частинок, у другому – 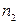 частинок і так далі. Вважаючи частинки тотожними і невзаємодіючими (ідеальний газ) констатуємо, що ці індивідуальні стани не інтерферують, а сам набір станів
частинок і так далі. Вважаючи частинки тотожними і невзаємодіючими (ідеальний газ) констатуємо, що ці індивідуальні стани не інтерферують, а сам набір станів 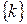 є однаковим для кожної частинки. Тоді хвильову функцію
є однаковим для кожної частинки. Тоді хвильову функцію 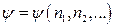 можна зобразити як добуток індивідуальних для кожного стану хвильових функцій:
можна зобразити як добуток індивідуальних для кожного стану хвильових функцій: 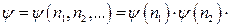
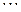 . При цьому
. При цьому
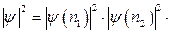
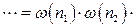
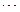 , (14.12)
, (14.12)
де 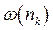 – ймовірність знаходження у k-му стані рівно
– ймовірність знаходження у k-му стані рівно 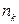 частинок.
частинок.
Величина 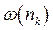 і є тим квантовим розподілом ймовірностей за числами заповнення
і є тим квантовим розподілом ймовірностей за числами заповнення 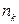 , за допомогою якого можна одержати спостережувальні характеристики ідеального газу. Для визначення
, за допомогою якого можна одержати спостережувальні характеристики ідеального газу. Для визначення 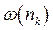 розглянемо квантовий великий канонічний розподіл (14.10). Врахуємо, що
розглянемо квантовий великий канонічний розподіл (14.10). Врахуємо, що 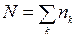 і
і 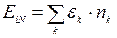 , де
, де 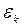 – енергія k-го індивідуального стану. Це дозволяє записати
– енергія k-го індивідуального стану. Це дозволяє записати
|ψ|2 = 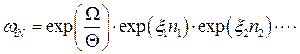 , (14.13)
, (14.13)
де 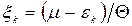 . Зазначимо, що набір квантових чисел і визначається послідовністю чисел заповнення
. Зазначимо, що набір квантових чисел і визначається послідовністю чисел заповнення 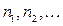 , яка може бути довільною в межах
, яка може бути довільною в межах 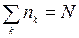 . Порівнюючи (14.13) з (14.12), бачимо, що з точністю до нормуючого множника
. Порівнюючи (14.13) з (14.12), бачимо, що з точністю до нормуючого множника
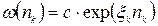 . (14.14)
. (14.14)
Оскільки для довільного k повинно виконуватись 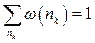 , маємо
, маємо 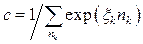 та
та
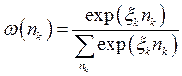 . (14.15)
. (14.15)
Середнє число частинок 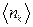 (спостережувальна величина) у k-му стані дорівнюватиме
(спостережувальна величина) у k-му стані дорівнюватиме
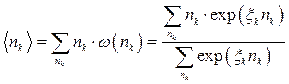 . (14.16)
. (14.16)
З фізичної точки зору 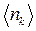 є розподілом середнього числа частинок за станами.
є розподілом середнього числа частинок за станами.
Для подальшого розрахунку величини 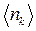 треба визначитися із значеннями, яких можуть набувати числа заповнення
треба визначитися із значеннями, яких можуть набувати числа заповнення 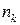 . Відомо, що для бозонів (частинки з цілим спіном) значення
. Відомо, що для бозонів (частинки з цілим спіном) значення 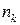 не мають обмежень, тобто
не мають обмежень, тобто 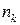 можуть дорівнювати 0; 1; 2; … . У той же час для ферміонів (частинки з напівцілим спіном) через принцип заборони Паулі
можуть дорівнювати 0; 1; 2; … . У той же час для ферміонів (частинки з напівцілим спіном) через принцип заборони Паулі 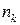 дорівнюють лише двом значенням: 0 та 1.
дорівнюють лише двом значенням: 0 та 1.
Отже, розглянемо спочатку випадок ідеального газу ферміонів. Для остаточного розрахунку 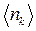 зобразимо розподіл (14.16) у вигляді
зобразимо розподіл (14.16) у вигляді
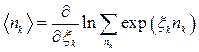 . (14.17)
. (14.17)
З урахуванням nk = 0; 1 матимемо
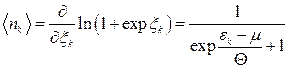 . (14.18)
. (14.18)
Розподіл (14.18) називається розподілом Фермі–Дірака.
Розглянемо тепер ідеальний газ бозонів. У цьому випадку сума у (14.17) є сумою нескінченно спадної геометричної прогресії (за умови 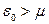 ), яка дорівнює
), яка дорівнює 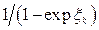 . Підставляючи цей вираз у (14.17), одержуємо розподіл Бозе–Ейнштейна
. Підставляючи цей вираз у (14.17), одержуємо розподіл Бозе–Ейнштейна
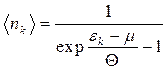 . (14.19)
. (14.19)
Оскільки кратність виродження 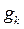 має зміст розподілу станів за енергією, помноживши розподіли (14.18) та (14.19) на
має зміст розподілу станів за енергією, помноживши розподіли (14.18) та (14.19) на 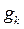 , матимемо квантові розподіли середнього числа частинок за енергією:
, матимемо квантові розподіли середнього числа частинок за енергією:
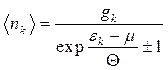 . (14.20)
. (14.20)
Для таких ферміонів, як електрони, прийнято виділяти з величини 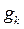 множник 2s + 1 = 2, який виражає фактор виродження за спіном (
множник 2s + 1 = 2, який виражає фактор виродження за спіном ( 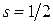 ).
).
Перехід до квазінеперервного спектру. Співставлення квантових та класичних розподілів.Через звичайно велику кількість частинок N енергетичний спектр, який нумерується квантовим числом k, виявляється досить щільним. Це дозволяє з достатньою точністю описати дискретний розподіл 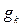 неперервною функцією, тобто провести у (14.20) заміну:
неперервною функцією, тобто провести у (14.20) заміну: 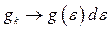 та
та 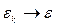 . Таку процедуру називають переходом до квазінеперервного спектру. При цьому
. Таку процедуру називають переходом до квазінеперервного спектру. При цьому 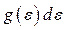 виражатиме кількість квантових станів, які припадають на енергетичний проміжок
виражатиме кількість квантових станів, які припадають на енергетичний проміжок 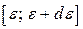 . Для підрахування величини
. Для підрахування величини 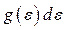 збагнемо, що у дискретизованому квантовому фазовому просторі цю кількість можна одержати поділивши фазовий об’єм, який відповідає проміжку
збагнемо, що у дискретизованому квантовому фазовому просторі цю кількість можна одержати поділивши фазовий об’єм, який відповідає проміжку 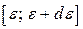 , на фазовий об’єм одного стану, тобто на
, на фазовий об’єм одного стану, тобто на 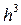 (маються на увазі об’єми, що припадають на одну частинку, оскільки вони пропорційні кількості останніх). Тоді у термінах
(маються на увазі об’єми, що припадають на одну частинку, оскільки вони пропорційні кількості останніх). Тоді у термінах 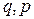 запишемо
запишемо
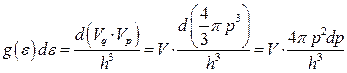 , (14.21)
, (14.21)
де 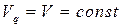 – звичайний координатний об’єм, який займає одна частинка, а
– звичайний координатний об’єм, який займає одна частинка, а 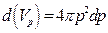 – об’єм кульового шару у імпульсному підпросторі. Переходячи до змінної
– об’єм кульового шару у імпульсному підпросторі. Переходячи до змінної 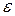 , з урахуванням
, з урахуванням 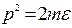 остаточно отримаємо
остаточно отримаємо
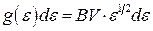 , (14.22)
, (14.22)
де 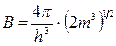 або
або 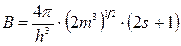 з урахуванням виродження за спіном. Отже, неперервні квантові розподіли середнього числа частинок ідеального газу за енергією матимуть вигляд
з урахуванням виродження за спіном. Отже, неперервні квантові розподіли середнього числа частинок ідеального газу за енергією матимуть вигляд
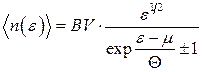 . (14.23)
. (14.23)
Корисно провести співставлення (14.23) з класичними розподілами. Якщо знехтувати одиницею у знаменнику, цей вираз перетворюється у класичний розподіл Максвелла за кінетичною енергією (див. задачу 2). Така обставина дозволяє визначити термодинамічні умови, коли можна користуватися класичною статистикою, і навпаки – коли стає необхідним квантовий підхід. Дійсно, знехтувати доданком ±1 у (14.23) припустимо, якщо 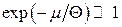 або
або 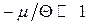 . Ці посилені нерівності називають критеріями невиродженості. Обернені їм нерівності називають критеріями сильного виродження. Експоненціальний множник
. Ці посилені нерівності називають критеріями невиродженості. Обернені їм нерівності називають критеріями сильного виродження. Експоненціальний множник 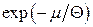 називають фактором виродження. Повернемося до нерівності
називають фактором виродження. Повернемося до нерівності 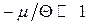 і прослідкуємо низку рівностей, виходячи з того, що
і прослідкуємо низку рівностей, виходячи з того, що 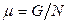 (
( 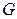 – потенціал Гіббса):
– потенціал Гіббса):
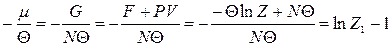 .
.
Звідси випливає наслідок критерію невиродженості: 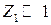 або, враховуючи (13.5),
або, враховуючи (13.5), 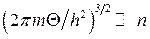 і остаточно
і остаточно
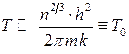 . (14.24)
. (14.24)
Температуру 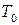 називають температурою виродження. Як бачимо, вона задає у певній мірі проміжну термодинамічну умову між областями, у яких можна користуватися класичною, а в яких – квантовою статистиками. Важливо відмітити, що величина
називають температурою виродження. Як бачимо, вона задає у певній мірі проміжну термодинамічну умову між областями, у яких можна користуватися класичною, а в яких – квантовою статистиками. Важливо відмітити, що величина 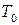 залежить від густини частинок
залежить від густини частинок 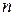 та їх маси
та їх маси 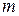 . Так, для електронного газу у металах (
. Так, для електронного газу у металах ( 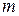 ~
~ 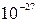 г,
г, 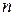 ~
~ 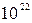 см–3) маємо
см–3) маємо 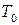 ~
~ 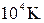 , тобто такий газ завжди сильно вироджений і повинен описуватися квантовою статистикою. Для напівпровідників
, тобто такий газ завжди сильно вироджений і повинен описуватися квантовою статистикою. Для напівпровідників 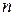 ~
~ 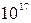 см–3, звідки
см–3, звідки 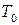 ~
~ 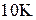 . Тому електронний газ у напівпровідниках при кімнатних температурах є невиродженим і в цих умовах можна користуватися класичними розподілами. Для звичайних газів
. Тому електронний газ у напівпровідниках при кімнатних температурах є невиродженим і в цих умовах можна користуватися класичними розподілами. Для звичайних газів 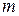 ~
~ 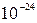 г і
г і 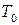 ~ 1K; це говорить про те, що вони практично завжди невироджені.
~ 1K; це говорить про те, що вони практично завжди невироджені.
Квантові ідеальні гази при низьких температурах. Сильно вироджений електронний газ.При достатньо низьких температурах( 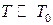 ), коли починають виявлятися квантові особливості ідеальних газів, стає суттєво різною поведінка фермі- та бозе-систем. Розглянемо спочатку сильно вироджений електронний газ. Термодинамічні внутрішню енергію
), коли починають виявлятися квантові особливості ідеальних газів, стає суттєво різною поведінка фермі- та бозе-систем. Розглянемо спочатку сильно вироджений електронний газ. Термодинамічні внутрішню енергію 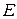 та кількість частинок
та кількість частинок  запишемо як середні за розподілом Фермі–Дірака (14.23):
запишемо як середні за розподілом Фермі–Дірака (14.23):
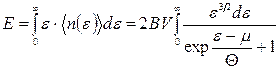 , (14.24)
, (14.24)
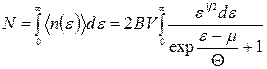 . (14.25)
. (14.25)
Ці формули неявно визначають залежність величин 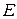 і
і 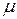 від параметрів системи
від параметрів системи 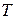 ,
, 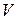 ,
,  . Тому наступною задачею буде, хоча б приблизно, одержати таку залежністьу явному вигляді.
. Тому наступною задачею буде, хоча б приблизно, одержати таку залежністьу явному вигляді.
За умови сильного виродження 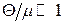 (або
(або 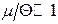 ) знайдемо вираз для величин
) знайдемо вираз для величин 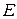 і
і  з (14.24) та (14.25) у вигляді розвинення у ряд за степенями мализни
з (14.24) та (14.25) у вигляді розвинення у ряд за степенями мализни 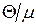 . Для цього розглянемо інтеграл
. Для цього розглянемо інтеграл
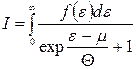 . (14.26)
. (14.26)
Запишемо його як суму
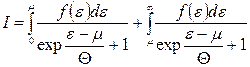 .
.
Оскільки
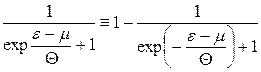 ,
,
маємо
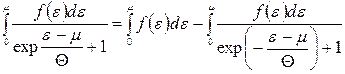 .
.
Отже, вираз (14.26) зобразимо у вигляді
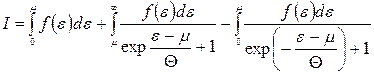 . (14.27)
. (14.27)
Зробимо у другому інтегралі (14.27) заміну 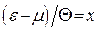 . Одержимо
. Одержимо
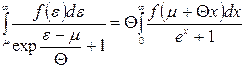 .
.
Аналогічна заміна 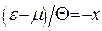 у третьому інтегралі (14.27) дає
у третьому інтегралі (14.27) дає
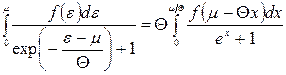 .
.
Як показує аналіз, заміна в останньому інтегралі верхньої межі 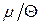 на нескінченність (пам’ятаємо умову
на нескінченність (пам’ятаємо умову 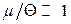 ) не впливає на шукане розвинення у ряд за степенями мализни
) не впливає на шукане розвинення у ряд за степенями мализни 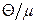 . Це дозволяє записати
. Це дозволяє записати  у вигляді
у вигляді
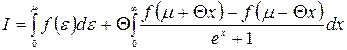 . (14.28)
. (14.28)
Обмежившись двома доданками у розвиненні чисельника за степенями 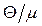 в останньому інтегралі, отримаємо
в останньому інтегралі, отримаємо
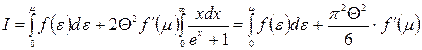 . (14.29)
. (14.29)
Врахувавши тепер, що для (14.24) 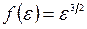 , а для (14.25)
, а для (14.25) 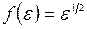 , після обчислення (14.29) матимемо шукані розкладання з точністю до
, після обчислення (14.29) матимемо шукані розкладання з точністю до 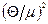 :
:
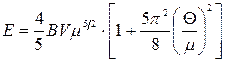 , (14.30)
, (14.30)
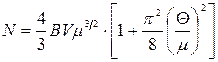 . (14.31)
. (14.31)
Математичний аналіз (14.31) дозволяє визначити наближену температурну залежність хімічного потенціалу μ в області сильного виродження. Дійсно, при 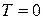 К з (14.31) одержуємо
К з (14.31) одержуємо
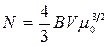 , (14.32)
, (14.32)
де μ0 – хімічний потенціал при 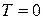 К. Розділивши (14.31) на (14.32), знайдемо
К. Розділивши (14.31) на (14.32), знайдемо
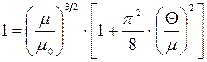 . (14.33)
. (14.33)
Оскільки 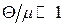 , в цій області температур у формулі (14.33) можна зробити заміну
, в цій області температур у формулі (14.33) можна зробити заміну 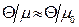 , звідки випливає
, звідки випливає
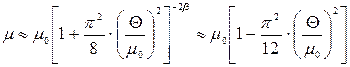 . (14.34)
. (14.34)
Звідси бачимо, що у розглядуваній області хімічний потенціал 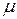 із зростанням
із зростанням 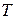 зменшується. Припущення
зменшується. Припущення 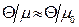 можна зробити і для (14.30). При цьому, розділивши (14.30) на (14.32), отримаємо
можна зробити і для (14.30). При цьому, розділивши (14.30) на (14.32), отримаємо
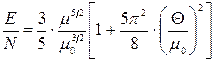
і остаточно з урахуванням (14.34)
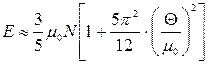 . (14.35)
. (14.35)
Формула (14.35) визначає середню (тобто термодинамічну) енергію електронного газу як функцію 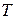 ,
, 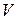 ,
,  в умовах сильного виродження. В цій області методами вже самої термодинаміки можна знайти довільні властивості такої системи (
в умовах сильного виродження. В цій області методами вже самої термодинаміки можна знайти довільні властивості такої системи ( 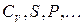 ).
).
До речі, молярна теплоємність
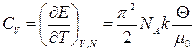
електронного газу в металі при 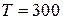 К дорівнює ~ 0,05 кал/моль, що на два порядки менше, ніж у класичного одноатомного газу. Це свідчить саме про квантові властивості електронного газу в даних умовах.
К дорівнює ~ 0,05 кал/моль, що на два порядки менше, ніж у класичного одноатомного газу. Це свідчить саме про квантові властивості електронного газу в даних умовах.
На закінчення відмітимо, що так звана нульова енергія 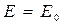 електронного газу при
електронного газу при 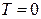 К залишається скінченною:
К залишається скінченною: 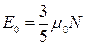 . Це зумовлено принципом заборони Паулі, згідно з яким лише два ферміони можуть займати стан з певною енергією. Тому, починаючи з
. Це зумовлено принципом заборони Паулі, згідно з яким лише два ферміони можуть займати стан з певною енергією. Тому, починаючи з 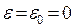 , кожна така пара (навіть при
, кожна така пара (навіть при 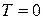 К) прирощуватиме свою енергію стан від стану. Аналіз розподілу Фермі–Дірака за станами (14.18) для вже розщепленого за спіном енергетичного спектру
К) прирощуватиме свою енергію стан від стану. Аналіз розподілу Фермі–Дірака за станами (14.18) для вже розщепленого за спіном енергетичного спектру 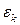 показує, що при
показує, що при 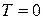 К (а при цьому
К (а при цьому 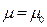 ) максимальна енергія електрона, при якій ще
) максимальна енергія електрона, при якій ще 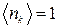 , дорівнює
, дорівнює 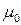 . Ця енергія називається енергією Фермі. Їй відповідає деякий стан з квантовим числом
. Ця енергія називається енергією Фермі. Їй відповідає деякий стан з квантовим числом 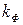 (див. задачу 2). З (14.32) бачимо, що
(див. задачу 2). З (14.32) бачимо, що
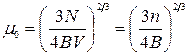 . (14.36)
. (14.36)
Для електронного газу в металі ( 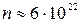 см–3)
см–3) 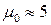 еВ
еВ 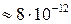 ерг.
ерг.
Квантові ідеальні гази при низьких температурах. Вироджений бозе-газ.Розглянемо тепер властивості бозе-газу при низьких температурах в області виродження, коли
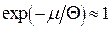 або
або 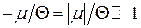 . (14.37)
. (14.37)
Тут ми виходимо з того, що для існування точного розподілу Бозе–Ейнштейна (14.19) хімічний потенціал 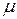 повинен бути суттєво від’ємним (
повинен бути суттєво від’ємним ( 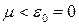 ). Інакше ряд у (14.17) розбігатиметься, що відповідатиме відсутності рівноважного стану в ідеальному бозе-газі. Квазінеперервне наближення (14.23) допускає значення
). Інакше ряд у (14.17) розбігатиметься, що відповідатиме відсутності рівноважного стану в ідеальному бозе-газі. Квазінеперервне наближення (14.23) допускає значення 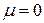 , але при
, але при 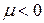 формула
формула
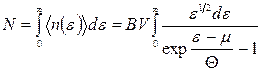 (14.38)
(14.38)
для повного числа частинок не дає через інтеграл якогось внеску у  в околі
в околі 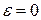 . При
. При 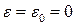 точне середнє число частинок
точне середнє число частинок 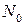 в цьому стані за формулою (14.19) дорівнюватиме
в цьому стані за формулою (14.19) дорівнюватиме
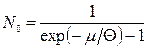 .
.
Тому природно доповнити цією кількістю число  з (14.38):
з (14.38):
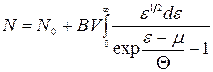 . (14.39)
. (14.39)
Оскільки 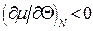 (див. задачу 3), тобто при зменшенні температури хімічний потенціал може зростати до 0, залишаючись від’ємним, існуватиме певна температура
(див. задачу 3), тобто при зменшенні температури хімічний потенціал може зростати до 0, залишаючись від’ємним, існуватиме певна температура 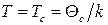 , нижче якої виконуватиметься умова (14.37). При цьому можна наближено записати
, нижче якої виконуватиметься умова (14.37). При цьому можна наближено записати
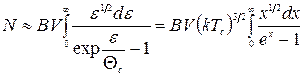 ; (14.40)
; (14.40)
цей невласний інтеграл дорівнює 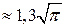 . З (14.40) маємо значення
. З (14.40) маємо значення 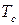 :
: 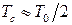 , де
, де 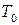 – температура виродження. Однак у проміжку
– температура виродження. Однак у проміжку 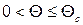 і (14.39), залишаючи температурну залежність, можна записати як
і (14.39), залишаючи температурну залежність, можна записати як
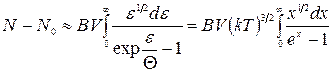 . (14.41)
. (14.41)
Розділивши (14.41) на (14.40), отримаємо так званий закон трьох других квантової статистики
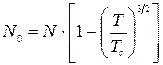 , (14.42)
, (14.42)
який виражає кількісне накопичування бозонів (від загальної їх кількості) на нульовому енергетичному рівні нижче температури 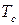 . Як бачимо з (14.42), в цій області температур число частинок на найнижчому рівні стає порівняним з повною їх кількістю. Таке явище називають бозе-ейнштейнівською конденсацією, а
. Як бачимо з (14.42), в цій області температур число частинок на найнижчому рівні стає порівняним з повною їх кількістю. Таке явище називають бозе-ейнштейнівською конденсацією, а 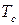 – температурою бозе-конденсації.
– температурою бозе-конденсації.
Термодинамічні властивості бозе-газу нижче температури 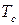 можна знайти, обчисливши внутрішню енергію (з наступним вирахуванням довільних параметрів):
можна знайти, обчисливши внутрішню енергію (з наступним вирахуванням довільних параметрів):
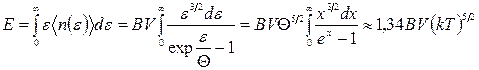 . (14.43)
. (14.43)
