Описание лабораторного макета. Лабораторная работа выполняется на компьютере с использованием виртуального макета, структурную схему которого приведено на рис

Лабораторная работа выполняется на компьютере с использованием виртуального макета, структурную схему которого приведено на рис. 1.

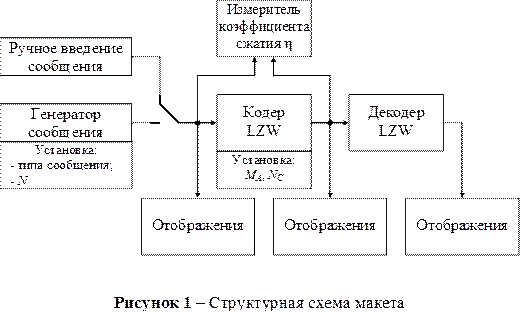
Макет в зависимости от пункта исследований автоматически переключается или в пошаговый режим, или в режим реального времени. Также в зависимости от пункта исследований включается ручное введение сообщения или генератор сообщения. Генератор сообщения позволяет выбирать один из двух типов сообщения и изменять длину сообщения N в пределах от 1 до 10000 символов. Реализация кодера позволяет выбирать одно из пяти значений объема словаря M_А и изменять максимальную длину строки в словаре N_C в пределах от 6 до 250.

Требования к отчету

7.1 Название лабораторной работы.

7.2 Цель работы.

7.3 Результаты выполнения домашнего задания.

7.4 Структурные схемы исследований и результаты выполнения пп. 5.2...5.7 лабораторного задания (таблицы и графики с подписями).

7.5 Выводы по каждому пункту задания, в которых предоставить анализ полученных результатов (совпадение теоретических и экспериментальных данных).

7.6 Дата, подпись студента, виза преподавателя с оценкой в 100-балльной системе.

ЛР 2.4 Дискретизация первичных
сигналов электросвязи

Цель работы

Изучение процесса дискретизации непрерывных во временем сигналов и способа восстановления их по отсчетам. Анализ характеристик дискретных сигналов и факторов, которые вызывают погрешности при восстановлении непрерывных сигналов.

Ключевые положения

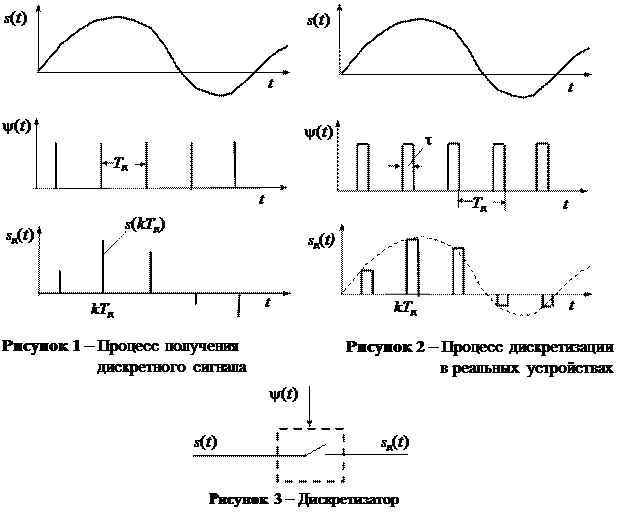
2.1 Дискретизация непрерывных по времени сигналов. Под дискретизацией непрерывного по времени сигнала s(t) понимают представление сигнала его мгновенными значениями (отсчетами) s(kT_д), где k = …, – 1, 0, 1, 2, …; T_д – интервал дискретизации. Последовательность отсчетов на графиках изображают вертикальными линиями высотой s(kT_д) каждая (рис. 1) и называют ее дискретным сигналом s_д(t).

В реальных устройствах отсчет сигнала s(kT_д) – это импульс с амплитудой s(kT_д) и длительностью t £ T_д, начинающийся в момент времени kT_д (рис. 2). Но, обычно, t << T_д. Устройство, формирующее отсчеты, называется дискретизатором. В случае t << T_д дискретизатор – это ключ, который замыкает цепь от источника к нагрузке на время t (рис. 3).

Аналитическое выражение дискретного сигнала s_д(t):

s_д(t) = s(t) y(t) = s(t) 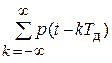, (1)

где y(t) – последовательность отсчетных импульсов, определяющая моменты времени, в которые берутся отсчеты сигнала, и их длительность;

р(t) – отсчетный импульс:

р(t) = 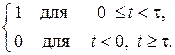(2)

2.2 Спектр дискретного сигнала. Преобразование Фурье правой части выражения (1) определяет спектральную плотность S_д(j2pf) дискретного сигнала (соответствующие математические выкладки можно найти в [1, с. 37, 38]):

S_д(j2pf) = 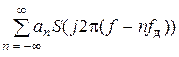, – ¥ < f < ¥, (3)

где f_д = 1/ T_д – частота дискретизации;

a_n = 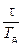× 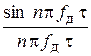– (4)

коэффициенты разложения импульса р(t) в ряд Фурье; поскольку t << T_д, то для малых значений n коэффициенты практически не зависят от n, т.е. a_n = t/Т_д;

S(j2pf) – спектральная плотность непрерывного сигнала s(t).

Из выражения (3) вытекает, что спектр дискретного сигнала – это сумма спектров S(j2pf) непрерывного сигнала s(t), смещенных на величину f_д и убывающих с увеличением n согласно выражению (4).

Для первичных сигналов электросвязи характерно, что их спектры прилегают к нулевой частоте. На рис. 4, а приведен амплитудный спектр произвольной формы S(f) первичного сигнала, который простирается до максимальной частоты F_max. Дальше на рис. 4 изображенные амплитудные спектры сигналов, которые могут иметь место при дискретизации сигнала со спектром, приведенным на рис. 4, а:

рис. 4, б – спектр S_y(f) последовательности отсчетных импульсов y(t), построенный на основе представления y(t) рядом Фурье:

y(t) = 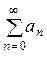×cos 2pnf_дt;

рис. 4, в – спектр S_д(f) дискретного сигнала, когда f_д > 2F_max;

рис. 4, г – спектр S_д(f), когда f_д = 2F_max;

рис. 4, д – спектр S_д(f), когда f_д < 2F_max.

2.3 Восстановление сигналов по их отсчетам. Согласно теореме Котельникова любой сигнал с ограниченным спектром можно точно восстановить (интерполировать) за его отсчетам, взятыми через интервал T_д £ 1/(2F_max), где F_max – максимальная частота спектра сигнала.

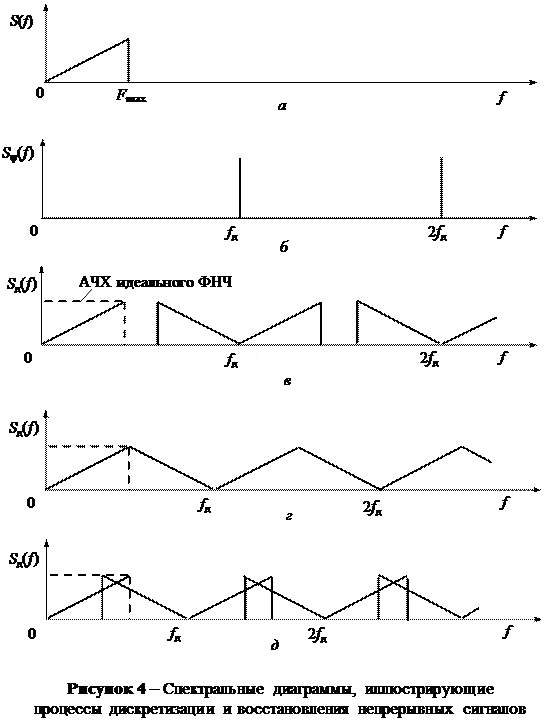В справедливости теоремы Котельникова легко убедиться, рассмотрев рис. 4, в, г, д. Если f_д ³ 2 F_max (рис. 4, в, г), то после подачи дискретного сигнала на вход идеального ФНЧ с частотой среза F_max £ F_ср £ f_д – F_max на выходе получим сигнал со спектром S(f) (рис. 4, в, г), т.е. восстановленный непрерывный сигнал. На рисунках штриховыми линиями показана АЧХ идеального ФНЧ с частотой среза F_ср = F_max. Если же f_д < 2F_max, то, как видно из рис. 4, д, невозможно выделить спектр S(f), поскольку имеет место перекрытие спектров.

Процесс восстановления непрерывного сигнала по его отсчетам можно трактовать и во временной области. Если для восстановления сигнала используется идеальный ФНЧ с частотой среза F_ср, то его импульсный отклик (без учета задержки в фильтре):

g(t) = 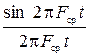. (5)

Поскольку отсчетные импульсы короткие (t << T_д) (приближаются к d-функции), то можно считать, что отклик ФНЧ на импульс с амплитудой s(kT_д), поданный в момент t = kT_д, имеет вид

s(kT_д) = 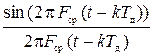. (6)

Если подать на вход ФНЧ сигнал s_д(t), на его выходе получим сумму откликов

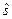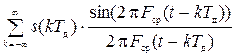(t) = . (7)

Сравним это выражение с рядом Котельникова,являющимся математическим выражением теоремы Котельникова,

s(t) = 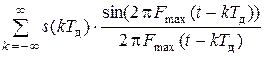. (8)

Если F_ср = F_max, то s(t) = 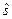(t), т.е. имеет место точное восстановление непрерывного сигнала.

2.4 Погрешности, которые возникают при восстановлении сигналов.

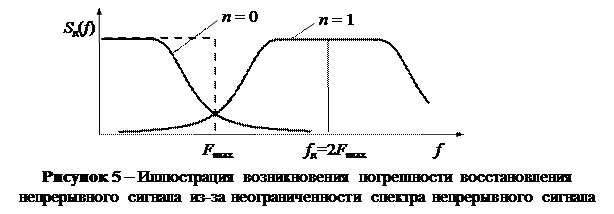
2.4.1 Неограниченность спектров реальных сигналов. Реальных сигналов со строго ограниченным спектром не существует, поскольку сигналы с конечной длительностью имеют неограниченные спектры – когда f ® ¥, спектры убывают с конечной скоростью. Для реальных сигналов максимальная частота спектра F_max определяется из условия, что составляющие с частотами f > F_max малые (в определенном смысле). В спектрах реальных дискретных сигналов возникает перекрытие спектров, по крайней мере, составляющих суммы (3) с индексами n = 0 i n = 1 (рис. 5). Предположим, что для восстановления непрерывного сигнала используется идеальный ФНЧ с частотой среза F_ср = F_max, его АЧХ показана пунктирной линией на рис. 5. Восстановленный сигнал будет иметь две составляющие погрешности восстановления:

– линейные искажения за счет отсечения составляющих сигнала s(t) с частотами f > F_max;

– наложение составляющих спектра S(f – f_д) с частотами f < F_max на спектр сигнала s(t) (погрешность наложения спектров).

С учетом сказанного значения F_max и f_д определяют из условия, чтобы погрешность восстановления была достаточно малой.

2.4.2 Отклонение характеристик реального ФНЧ от идеального. В идеального ФНЧ АЧХ имеет прямоугольную форму, а ФЧХ – линейную. Т.е., идеальный ФНЧ без искажений пропускает все составляющие спектра сигнала в пределах полосы пропускания, когда f < F_ср, и полностью ослабляет составляющие с частотами f > F_ср. Реальные ФНЧ описываются граничной частотой полосы пропускания F_пп и граничной частотой полосы задерживания F_пз (рис. 2.6, б).

Если ФНЧ предназначен для восстановления непрерывного сигнала с максимальной частотой F_max из дискретного сигнала с частотой дискретизации f_д, то необходимо, чтобы F_пп ³ F_max и F_пз £ f_д – F_max. В случае реальных ФНЧ могут возникать две составные погрешности восстановления:

– через непостоянство АЧХ и нелинейность ФЧХ в полосе пропускания фильтр вносит линейные искажения в восстановленный сигнал;

– через недостаточное ослабление в полосе задержания ФНЧ пропускает составляющие сигнала s_д(t) с частотами f > f_д – F_max, которые образуют погрешность наложения спектров.

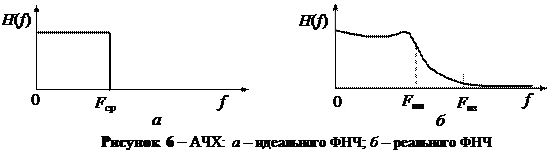Реальные ФНЧ для восстановления непрерывных сигналов проектируют так, чтобы погрешность восстановления была достаточно малой.

Ключевые вопроса

3.1 Объяснить физическую суть дискретизации по времени непрерывных сигналов.

3.2 С какой целью выполняется дискретизация непрерывных сигналов?

3.3 Объяснить связь спектров непрерывного и дискретного сигналов.

3.4 Объяснить физическую суть процесса восстановления сигнала по отсчетам.

3.5 Сформулировать теорему Котельникова.

3.6 Записать ряд Котельникова для сигнала с ограниченным спектром.

3.7 В чем заключаются основные отличия АЧХ и ФЧХ идеального и реального ФНЧ?

3.8 Какие причины погрешностей, которые возникают при восстановлении сигнала по отсчетам?

Домашнее задание

4.1 Изучить раздел “Дискретизация непрерывных сигналов” по конспекту лекций и литературе [1, с. 37...39; 3, с. 33...42; 4, с. 44...49] и описанию лабораторного макета в разд. 6.

4.2 Сигнал s(t) = A₁sin 2pf₁t + A₂sin 2pf₂t + A₃sin 2pf₃t дискретизируется с частотой f _д. Изобразить спектр сигнала S(f ) и спектр дискретного сигнала S_д(f) в диапазоне частот 0 < f < 2 f_д. Исходные данные сигнала согласно номеру Вашей бригады указаны в табл. 1.

Таблица 1 – Исходные данные к домашнему заданию

Номер бригады	А1, В	f1, кГц	А2, В	f2, кГц	А3, В	f3, кГц	fд, кГц
1, 9						1,5
2, 10				2,5		1,5	5,5
3, 11		0,5		1,5	3,5	2,5
4, 12				1,5	2,5	2,5	6,5
	2,5	0,5		2,5
	1,5			2,5			7,5
	3,5	0,5
		0,5			3,5

4.3 Рассчитать и построить график импульсного отклика идеального ФНЧ с частотой среза F_ср = f_д /2 для значений t в интервале (– 4T_д, 4T_д) (значение f_д взять из табл. 1).

4.4 Подготовиться к обсуждению по ключевым вопросам.

Лабораторная задача

5.1 Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 2.4 Дискретизация первичных сигналов электросвязи, используя иконку Лабораторные работы на рабочем столе, а затем папки ТЭС и Модуль 2. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.2 Провести исследование процесса дискретизации во временной и частотной областях.Для этого:

– установить значения A₁, f ₁, A₂, f ₂, A₃, f ₃ и частоту f _д такие же, как и в домашнем задании;

– назначить вход ФНЧ от дискретизатора и запустить программу на выполнение;

– зарисовать в протоколе осциллограммы и спектрограммы сигналов на выходах источника и дискретизатора;

– сравнить рассчитанную в домашнем задании и полученную на компьютере спектрограммы, результаты сравнения занести к выводам протокола;

– увеличить на 1 кГц частоту дискретизации, зарисовать в протоколе спектрограмму сигнала на выходе дискретизатора, изменения в спектрограмме занести к выводам протокола.

5.3 Провести исследование импульсного отклика восстанавливающего ФНЧ. Для этого:

– назначить подачу на вход ФНЧ d-импульса и установить значение частоты среза ФНЧ, заданной в домашнем задании;

– занести в протокол импульсный отклик и АЧХ ФНЧ, сравнить импульсный отклик ФНЧ с рассчитанным в домашнем задании.

– установить значение частоты среза ФНЧ вдвое меньшую, занести в протокол импульсный отклик и АЧХ ФНЧ для этого случая, характер изменений в импульсном отклике объяснить в выводах протокола.

5.4 Провести исследование процесса восстановления непрерывного сигнала во временной и частотной областях. Для этого:

– установить параметры A₁, f ₁, A₂, f ₂, A₃, f ₃ и частоту f _д такие же, как и в домашнем задании, установить частоту среза ФНЧ F_ср = f_д/2;

– назначить вход ФНЧ от дискретизатора и запустить программу на выполнение;

– сравнить осциллограммы и спектры на выходе ФНЧ и на выходе источника, результаты сравнения занести к выводам протокола;

– повторить это исследование дважды при следующих условиях: f_д = F_max и f _д = F_max – 0,2 кГц (F_max – максимальная частота в спектре непрерывного сигнала), каждый раз устанавливать частоту среза ФНЧ F_ср = f _д/2; в обеих случаях зарисовать осциллограммы и спектрограммы на выходе ФНЧ, в выводах описать характер погрешностей, объяснить причины их возникновения.