Задачи для контрольных работ 3 страница

2.73В двух сосудах одного и того же объема находятся различные идеальные газы (водород и кислород). Масса первого газа m₁ = 100 г, второго – m₂ = 100 г. Давления и температуры газов одинаковы. Сосуды соединяют, и начинается процесс диффузии. Определить изменение энтропии рассматриваемой системы.

2.74Кислород массой 1 кг занимает объем V₀. Определить вероятность самопроизвольного изотермического сжатия кислорода на 10^–6 часть первоначального объема.

2.75640 г расплавленного свинца при температуре плавления вылили на лед при 0 °C. Найти изменение энтропии при этом процессе.

2.76Какова средняя арифметическая скорость 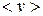молекул кислорода при нормальных условиях, если известно, что средняя длина свободного пробега 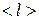молекулы кислорода при этих условиях равна 100 нм?

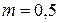2.77В сосуде вместимостью л находится водород массой г. Определить среднюю длину свободного пробега 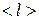молекулы водорода в этом сосуде.

2.78Средняя длина свободного пробега 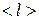молекулы водорода при некоторых условиях равна 2 мм. Найти плотность водорода при этих условиях.

2.79Водород находится под давлением 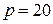мкПа и имеет температуру К. Определить среднюю длину свободного пробега 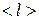молекулы такого газа.

2.80Кислород находится под давлением 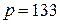нПа при температуре К. Вычислить среднее число 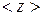столкновений молекулы кислорода при этих условиях за время 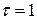с.

2.81При каком давлении р средняя длина свободного пробега 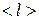молекул азота равна 1 м, если температура газа 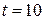°С?

2.82Найти среднее число 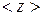столкновений за время 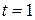с и длину свободного пробега 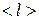молекулы гелия, если газ находится под давлением кПа при температуре К.

2.83Найти массу m воды, вошедшей в стеклянную трубку с диаметром канала 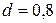мм, опущенную в воду на малую глубину. Считать смачивание полным.

2.84Какую работу А надо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от 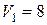см³ до 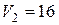см³? Считать процесс изотермическим.

2.85Пространство между двумя стеклянными параллельными пластинками с площадью поверхности 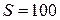см² каждая, расположенными на расстоянии 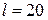мкм друг от друга, заполнено водой. Определить силу F, прижимающую пластинки друг к другу. Считать мениск вогнутым с диаметром d, равным расстоянию между пластинками.

2.86Глицерин поднялся в капиллярной трубке диаметром канала 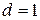мм на высоту 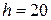мм. Определить поверхностное натяжение глицерина. Считать смачивание полным.

2.87В воду опущена на очень малую глубину стеклянная трубка с диаметром канала 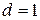мм. Определить массу воды, вошедшей в трубку.

2.88На сколько давление р воздуха внутри мыльного пузыря больше нормального атмосферного давления , если диаметр пузыря 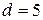мм?

2.89Воздушный пузырек диаметром 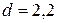мкм находится в воде у самой ее поверхности. Определить плотность воздуха в пузырьке, если воздух над поверхностью воды находится при нормальных условиях.

2.90Две капли ртути радиусом 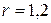мм каждая слились в одну большую каплю. Определить энергию 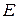, которая выделится при этом слиянии. Считать процесс изотермическим.

3.1Точечные заряды Q₁ = 20 мкКл, Q₂ = –10 мкКл находятся на расстоянии d = 5 см. друг от друга. Определить напряженность поля в точке, удаленной на r₁ = 3 см от первого и на r₂ = 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд Q = 1 мкКл.

3.2Три одинаковых точечных заряда Q₁ = Q₂ = Q₃ = 2 нКл находятся в вершинах равностороннего треугольника со сторонами а = 10 см. Определить модуль и направление силы F, действующей на один из зарядов со стороны двух других.

3.3Два положительных точечных заряда Q и 9Q закреплены на расстоянии d = 100 см. друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения зарядов возможны только вдоль прямой, проходящей через закрепленные заряды.

3.4Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол 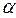. Шарики погружают в масло. Какова плотность 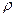масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков 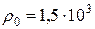кг/м³, диэлектрическая проницаемость масла 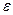= 2,2.

3.5Четыре одинаковых заряда Q₁ = Q₂ = Q₃ = Q₄ = 40 нКл закреплены в вершинах квадрата со стороной а = 10 см. Найти силу F, действующую на один из этих зарядов со стороны трех остальных.

3.6Точечные заряды Q₁ = 30 мкКл и Q₂ = –20 мкКл находятся на расстоянии d = 20 см друг от друга. Определить напряженность электрического поля Е в точке, удаленной от первого заряда на расстояние r₁ = 30 см, а от второго – на r₂ = 15 см.

3.7В вершинах правильного треугольника со стороной а = 10 см. Находятся заряды Q₁ = 10 мкКл, Q₂ = 20 мкКл и Q₃ = 30 мкКл. Определить силу F, действующую на заряд Q₁ со стороны двух других зарядов.

3.8В вершинах квадрата находятся одинаковые заряды Q₁ = Q₂ = Q₃ = Q₄ = 8×10^-10 Кл. Какой отрицательный заряд Q нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?

3.9На расстоянии d = 20 см находятся два точечных электрических заряда: Q₁ = –50 нКл и Q₂ = 100 нКл. Определить силу F,действующую на заряд Q₃ = –10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.

3.10Расстояние d между двумя точечными зарядами Q₁ = 2 нКл и Q₂ = 4 нКл равно 60 см. Определить точку, в которую нужно поместить третий заряд Q₃ так, чтобы система зарядов находилась в равновесии. Определить заряд Q₃ и его знак. Устойчивое или неустойчивое будет равновесие?

3.11Два шарика массой m = 1 г каждый подвешены на нитях, верхние концы которых соединены вместе. Длина каждой нити l = 10 см. Какие одинаковые заряды надо сообщить шарикам, чтобы нити разошлись на угол a = 60°?

3.12Расстояние между зарядами Q₁ = 100 нКл и Q₂ = –50 нКл равно d = 10 см. Определить силу F, действующую на заряд Q₃ = 1 мкКл, отстоящую от r₁ = 12 см от заряда Q₁ и на r₂ = 10 см от заряда Q₂.

3.13Два одинаковых положительных точечных заряда Q₁ = Q₂ = Q находятся на расстоянии 2l = 10 см друг от друга. На прямой, являющейся осью симметрии этих зарядов и перпендикулярной к линии, соединяющей центры зарядов, точку, в которой напряженность поля электрического поля имеет максимум.

3.14Два заряженных шарика одинаковых радиуса и массы подвешены на нитях одинаковой длины и опущены в керосин. Какова должна быть плотность r материала шариков, чтобы углы расхождения нитей в воздухе и в керосине были одинаковы?

3.15К заряженной бесконечной плоскости, расположенной вертикально, присоединен на нити заряженный шарик с массой m = 1 г и зарядом Q = 1 нКл. Какой угол a с плоскостью образует нить, на которой весит шарик, если на поверхности равномерно распределен заряд с поверхностной плотностью s = 40 мкКл/м²?

3.16Тонкий стержень длиной l = 20 см несет равномерно распределенный заряд 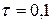мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см. от его конца.

3.17Тонкое кольцо несет распределенный заряд Q = 0,2 мкКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, равноудаленной от всех точек кольца на расстояние r = 20 см. Радиус кольца R = 10 см.

3.18Треть тонкого кольца радиуса R = 10 см несет распределенный заряд Q = 50 нКл. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке О, совпадающей с центром кольца.

3.19Бесконечный тонкий стержень, ограниченный с одной стороны, несет равномерно распределенный заряд с линейной плотностью 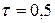мкКл/м. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, лежащей на оси стержня на расстоянии а = 20 см от его начала.

3.20По тонкому кольцу радиусом R = 20 см. равномерно распределен с линейной плотностью 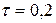мкКл/м заряд. Определить напряженность Е электрического поля, создаваемого распределенным зарядом в точке А, находящейся на оси кольца на расстоянии h = 2R от его центра.

3.21На двух концентрических сферах радиусом R и 2R равномерно распределены заряды с поверхностными плотностям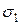и и 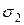(рис. 1). Требуется: 1) используя теорему Остроградского–Гаусса, найти зависимость Е(r) напряженности электрического поля от расстояния для трех областей: I, II, и III. Принять 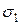= 4 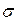, 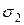= 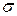; 2) вычислить напряженность Е в точке, удаленной от центра на расстояние r, и указать направление вектора 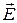. Принять 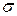= 30 нКл/м², r = 1,5R; 3) построить график Е(r).

3.22См. условие задачи 3.21. В п.1 принять s₁ = s, s₂ = –s. В п.2 принять s = 0,1 мкКл/м², r = 3R

3.23См. условие задачи 3.21. В п.1 принять s₁ = –4s, s₂ = s. В п.2 принять s = 50 нКл/м², r = 1,5R.

3.24См. условие задачи 3.21. В п.1 принять s₁ = –2s, s₂ = s. В п.2 принять s = 0,1 мкКл/м², r = 3R.

3.25На двух бесконечных параллельных плоскостях равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 2). Требуется: 1) используя теорему Остроградского – Гаусса и принцип суперпозиции электрических полей, найти выражение Е(х) напряженности электрического поля в трех областях: I, II и III. Принять s₁ = 2s, s₂ = s; 2) вычислить напряженность Е поля в точке, расположенной слева от плоскостей, и указать направление вектора Е; 3) построить график Е(х).

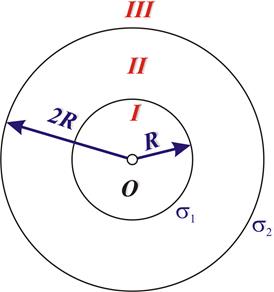
Рисунок 1

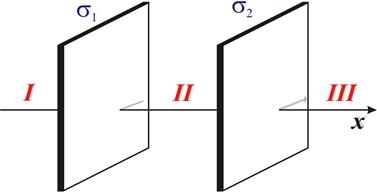
Рисунок 2

3.26См. условие задачи 3.25. В п.1 принять s₁ = –4s, s₂ = 2s. В п.2 принять s = 40 нКл/м² и точку расположить между плоскостями.

3.27См. условие задачи 3.25. В п.1 принять s₁ = s, s₂ = –2s. В п.2 принять s = 20 нКл/м² и точку расположить справа от плоскостей.

3.28На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями s₁ и s₂ (рис. 3). Требуется: 1) используя теорему Остроградского – Гаусса: найти зависимость Е (r) напряженности электрического поля от расстояния для трех областей: I, II и III. Принять s₁ = –2s, s₂ = s ; 2) вычислить напряженность Е в точке, удаленной от оси цилиндров на расстояние r, и указать направление вектора 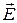. Принять s = 50 нКл/м², r = 1,5R; 3) построить график Е (r).

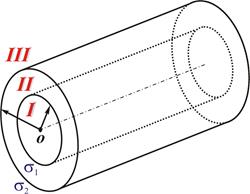
Рисунок 3

3.29См. условие задачи 3.28. В п.1 принять s₁ = s, s₂ = –s. В п.2 принять s = 60 нКл/м², r = 3R.

3.30См. условие задачи 3.28. В п.1 принять s₁ = –s, s₂ = 4s . В п.2 принять s = 30 нКл/м², r = 4R.

3.31Два точечных заряда 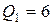нКл и 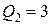нКл находятся на расстоянии d = 60 см друг от друга. Какую работу необходимо совершить внешним силам, чтобы уменьшить расстояние между зарядами вдвое?

3.32Электрическое поле создано заряженным проводящим шаром, потенциал 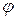которого 300 В. Определить работу сил поля по перемещению заряда Q = 0,2 мкКл из точки 1 в точку 2 (рис. 4).

Рисунок 4

3.33Электрическое поле создано зарядами Q₁ = 2 мкКл и Q₂ = –2 мкКл, находящимися на расстоянии а = 10 см. друг от друга. Определить работу сил поля, совершаемую при перемещении заряда Q = 0,5 мкКл из точки 1 в точку 2 (рис. 5).

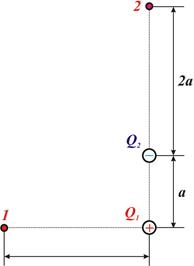
Рисунок 5

3.34Две параллельно заряженные плоскости, поверхностные плотности заряда которых s₁ = 2 мкКл/м² и s₂ = –0,8 мкКл/м², находятся на расстоянии d = 0,6 см. друг от друга. Определить разность потенциалов U между плоскостями.

3.35Диполь с электрическим моментом р = 100 пКл×м свободно установился в электрическом поле напряженностью Е = 200 кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол a = 180°.

3.36Четыре одинаковых капли ртути, заряженных до потенциала j = 10 В, сливаются в одну. Каков потенциал j₁ образовавшейся капли?

3.37Тонкий стержень согнут в кольцо радиусом R = 10 см. Он равномерно заряжен с линейной плотностью заряда t = 800 нКл/м. Определить потенциал j в точке, расположенной на оси кольца на расстоянии h = 10 см от его центра.

3.38Поле образовано точечным диполем с электрическим моментом р = 200 пКл×м. Определить разность потенциалов U двух точек поля, расположенных симметрично относительно диполя на его оси на расстоянии r = 40 см от центра диполя.

3.39Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой t = 20 пКл/м. Определить разность потенциалов U двух точек поля, отстоящих от нити на расстоянии r₁ = 8 см и r₂ = 12 см.

3.40Тонкая квадратная рамка равномерно заряжена с линейной плотностью заряда t = 200 пКл/м. Определить потенциал j поля в точке пересечения диагоналей.

3.41Одинаковые заряды q = 100 нКл расположены в вершинах квадрата со стороной а = 10 см. Определите потенциальную энергию той системы.

3.42Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью s = 1 нКл/м². Определите разность потенциалов между двумя точками этого поля, лежащими на расстоянии x₁ = 20 см и x₂ = 50 см от плоскости.

3.43Электростатическое поле создается шаром радиусом R = 8 см, равномерно заряженным с объемной плотностью r = 10 нКл/м³. Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии r₁ = 10 см и r₂ = 15 см от центра шара.

3.44Электростатическое поле создается бесконечным цилиндром радиусом R = 8 мм, равномерно заряженным с линейной плотностью t = 10 нКл/м. Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии r₁ = 2 мм и r₂ = 7 мм от поверхности этого цилиндра.

3.45Электростатическое поле создается сферой радиусом R = 5 см, равномерно заряженной с поверхностной плотностью s = 1 нКл/м². Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r₁ = 10 см и r₂ = 15 см от центра сферы.

3.46Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределенным зарядом (t = 10 нКл/м). Определить кинетическую энергию E_k1 электрона в точке, находящейся на расстоянии l₁ = a от линии, если в точке, удаленной на l₂ = 2a от линии его кинетическая энергия E_k2 = 200 эВ.

3.47Электрон, обладавший кинетической энергией E_k = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов U = 8 В?

3.48Найти отношение скоростей ионов Си⁺⁺ и К⁺, прошедших одинаковую разность потенциалов.

3.49Электрон с энергией E_k = 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 10 см. Найти минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее Q = –10 нКл.

3.50Электрон, пройдя в плоском конденсаторе путь от одной пластины до другой, приобрел скорость v = 10⁵ м/с. Расстояние между пластинами d = 8 мм. Найти: 1) разность потенциалов U между пластинами; 2) поверхностную плотность заряда s на пластинах.

3.51Пылинка массой т = 5 нг, несущая на себе N = 10электронов, прошла в вакууме ускоряющую разность потенциалов U = 1 МВ. Какова кинетическая энергия E_k пылинки? Какую скорость v приобрела пылинка?

3.52Какой минимальной скоростью v_min должен обладать протон, чтобы он мог достигнуть поверхности металлического шара, имеющего радиус R и заряженного до потенциала j = 400 B, начав двигаться из точки, удаленной на l = 3R от поверхности шара?

3.53В однородное электрическое поле напряженностью Е = 200 В/м влетает (вдоль силовой линии) электрон со скоростью v₀ = 2 Мм/с. Определить расстояние l, которое пройдет электрон до точки, в которой его скорость будет равна половине начальной.

3.54Пылинка массой т = 200 мкг, несущая на себе заряд Q = 40 нКл, влетела в электрическое поле в направлении силовых линий. После прохождения разности потенциалов U = 200 В пылинка имела скорость v = 10 м/с. Определить скорость v₀пылинки до того, как она влетела в поле.

3.55Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом ₁ = 100 В электрон имел скорость v₁ = 6 Мм/с. Определить потенциал 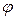₂ точки поля, дойдя до которой электрон потеряет половину своей скорости.

3.56Электрон, пролетая в электрическом поле, увеличил свою скорость с v₁ = 1000 км/с до v₂ = 3000 км/с. Найти ускоряющею разность потенциалов.

3.57Два одинаковых заряда q₁ = q₂ = 50 мкКл находятся на расстоянии r₁ = 1 м друг от друга. Какую работу надо совершить, чтобы сблизить их до расстояния r₂ = 0,5 м?

3.58Электрон с начальной скоростью v = 3 Мм/с влетел в однородное электрическое поле напряженностью E = 150 В/м. Вектор начальной скорости перпендикулярен линиям напряженности электрического поля. Определить скорость электрона через t = 0,1 мс.

3.59Какую ускоряющую разность потенциалов должен пройти электрон, чтобы получить скорость v = 8 Мм/с?

3.60Протон, летящий к неподвижному ядру двукратно ионизированного атома гелия, на очень большом расстоянии от ядра имеет скорость v₀ =10⁴ м/с. На какое расстояние протон сможет приблизиться к ядру, если ядро гелия все время остается неподвижным?

3.61Конденсаторы емкостью С₁ = 5 мкФ и С₂ = 10 мкФ заряжены до напряжений U₁ = 60 В и U₂ = 100 В соответственно. Определить напряжение на обкладках конденсаторов после их соединения обкладками, имеющими одноименные заряды.

3.62Конденсатор емкостью С₁ = 10 мкФ заряжен до напряжения U = 10 В. Определить заряд на обкладках этого конденсатора после того, как параллельно ему был подключен другой, незаряженный, конденсатор емкостью С₂ = 20 мкФ.

3.63Конденсаторы емкостями С₁ = 2 мкФ, С₂ = 5 мкФ и С₃ = 10 мкФ соединены последовательно и находятся под напряжением U = 850 В. Определить напряжение и заряд на каждом из конденсаторов.