Задачі для самостійного розв’язування. 4.1. Показати, що для будь-якого оборотного циклу Карно виконується рівність

4.1. Показати, що для будь-якого оборотного циклу Карно виконується рівність

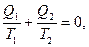
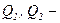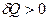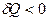де алгебраїчні значення кількості теплоти на ділянках і циклу відповідно.

4.2. Довести співвідношення (4.5).

4.3. Яким буде ККД циклу з задачі 6 цього розділу, якщо абсолютна температура лінійно зростає у 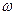разів із зменшенням ентропії? Який з цих двох циклів вигідніший?

4.4. Визначити максимальний ККД циклу, що має на діаграмі T, S форму еліпса з вісями, які паралельні вісям координат.

4.5. Яким буде ККД циклу з задачі 7, якщо на відповідній ділянці циклу температура зростає у 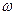разів?

4.6. Яким буде ККД циклу з задачі 2, якщо ділянку адіабатичного охолодження замінити процесом адіабатичного нагрівання?

4.7. Показати, що ККД циклу Стірлінга (див. задачу 3) менший за ККД циклу Карно з тими ж температурами холодильника і нагрівача. Які в цих умовах шляхи підвищення ККД циклу Стірлінга?

4.8. Яким буде ККД циклу з відомим відношенням w максимальної до мінімальної температур, якщо в умові задачі 2 адіабатичну ділянку замінити ізотермою?

4.9. Робочим тілом теплової машини є ідеальний газ. Визначити ККД циклу, що складається з ізобаричного, адіабатичного процесів і процесу ізотермічного розширення, якщо відоме відношення 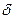максимального до мінімального тисків в циклі.

4.10. Визначити ККД циклу з ідеальним газом, що складається з ізобари, ізохори і процесу, в якому тиск лінійно зменшується із зростанням об’єму. Відомими вважати ступінь 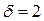збільшення тиску і ступінь 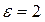стиснення газу в циклі.

Розділ 5

МЕДОД ТЕРМОДИНАМІЧНИХ ПОТЕНЦІАЛІВ

Теоретичні відомості

Внутрішня енергія як термодинамічний потенціал. У термодинаміці існують дваметоди дослідження багаточастинкових систем. Це метод циклів і метод термодинамічних потенціалів. Метод циклів оснований на дослідженні співвідношень між параметрами системи, які характерні для вибраного оборотного циклу, в рівняннях першого і другого начал. Найчастіше в цьому методі розглядається цикл Карно, для якого визначають ККД в загальному випадку за формулою 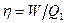, а потім прирівнюють його до 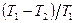і з отриманої рівності знаходять необхідну залежність. Метод циклів сформувався в роботах Карно, Клаузіуса, Нернста.

У сучасній термодинаміці майже в усіх випадках використовується метод термодинамічних потенціалів (в більш загальному формулюванні – метод характеристичних функцій), розвинений Гіббсом, на якому детально й зупинимось.

Вихідним у цьому методі є основне рівняння термодинаміки для рівноважних процесів (3.11). Проілюструємо сутність методу на прикладі простої системи з 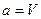і 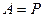. Тоді з (3.11) маємо:

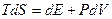. (5.1)

Ця рівність пов’язує п’ять термодинамічних параметрів. Разом з тим відомо, що стан простої системи визначається двома параметрами. Тому, вибираючи дві змінні з п’яти як незалежні, слід мати можливість знайти ще три величини, що залишились. З цією метою треба до (5.1) додати ще два рівняння. Якщо, скажімо, незалежними параметрами є 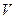і 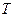, тоді додатковими до (5.1) можуть бути термічне 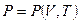і калоричне 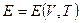рівняння стану.

Однак, при виборі довільної пари незалежних змінних рівняння (5.1) дозволяє знайти усі три невідомі функції, якщо до нього додати не два, а лише одне рівняння. Дійсно, нехай незалежними параметрами будуть об’єм 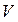і ентропія 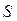. Тоді до (5.1) достатньо додати рівняння 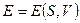, що визначає залежність внутрішньої енергії від 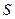і 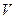. При цьому формально маємо:

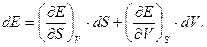(5.2)

Порівнюючи (5.1) і (5.2), знаходимо:

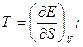
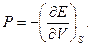(5.3)

Отже, за допомогою одного додаткового рівняння 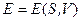ми, використовуючи (5.1), визначили формулами (5.3) решту два параметри: 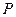і 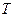. Крім того, диференціюючи (5.3) за 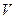першу рівність і за 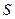другу, і прирівнюючи змішані похідні, отримаємо

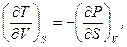(5.4)

а також в оберненому вигляді:

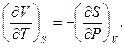(5.5)

Рівності (5.4), (5.5) називають співвідношеннями Максвелла. Вони фактично пов’язують дві властивості системи: її поведінку при адіабатичному розширенні і поведінку при ізохорній зміні тиску. Важливо звернути увагу на те, що співвідношення (5.4) і (5.5) є наслідком властивостей повного диференціала 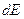функції 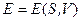і зовсім не потребують знання явного вигляду цієї функції.

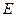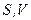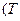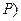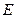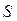Отже, внутрішня енергія при незалежних змінних є, як кажуть, характеристичною функцією. Це означає, що інші змінні і визначаються диференціюванням за і 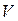відповідно. Крім того, перші похідні від 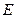визначають всі термічні властивості системи, а другі похідні – калоричні властивості. Так, наприклад, з першої рівності (5.3) маємо:

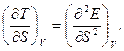(5.6)

З урахуванням 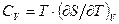для такої калоричної властивості, як теплоємність при постійному об’ємі з (5.3) і (5.6) отримаємо:

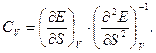(5.7)

Через те, що при :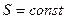

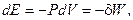
тобто за цих умов робота системи дорівнює зменшенню її внутрішньої енергії, характеристичну функцію 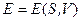називають також термодинамічним потенціалом. Термін “потенціал” тут позичений з ньютонової механіки, дякуючи повній аналогії між другим співвідношенням (5.3) і класичним зв’язком узагальненої сили 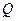з потенціальною енергією 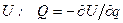, де 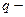відповідна 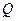узагальнена координата.

З (5.1) можна побачити, що формально об’єм 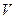(при незалежних змінних 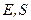) і ентропія 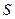(в змінних 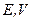) також будуть мати властивості характеристичної функції, хоча і не будуть при цьому термодинамічними потенціалами.

Вільна енергія. Якщо незалежними параметрами простої системи є не 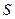і 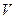, а друга пара змінних, внутрішня енергія 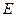вже не буде характеристичною функцією. Перетворення Лежандра (1.12) дозволяє на підставі (5.1) послідовно визначити термодинамічні потенціали для інших пар незалежних параметрів: (V,T), (T,P), (P,S). Так, для першої з перерахованих пар термодинамічним потенціалом буде алгебраїчна конструкція

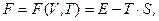(5.8)

яка називається вільною енергією (енергією Гельмгольца) системи. Дійсно, з (5.8) з урахуванням (5.1) маємо:

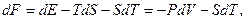(5.9)

що й визначає величину 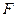як характеристичну функцію змінних 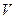і 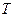. Далі, через те, що 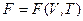, аналогічно (5.2) формально запишемо:

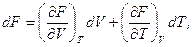(5.10)

звідки, порівнюючи з (5.9), знаходимо:

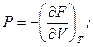
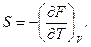(5.11)

Отже, в умовах, коли незалежними параметрами є 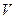і 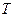, диференціал вільної енергії виражається через диференціали цих змінних, що і забезпечує визначення спряжених до 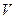і 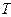величин частинними похідними (5.11). Наведемо приклади виразу через 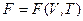таких властивостей, як теплоємність 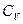і коефіцієнт стиску 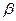. З результату задачі 1 глави 3 і другої рівності (5.11) випливає

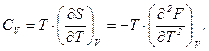(5.12)

За допомогою першої рівності (5.11) також знаходимо:

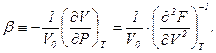(5.13)

Наступна пара співвідношень Максвелла випливає з (5.11) шляхом диференціювання цих рівностей: за 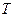першої рівності і за 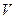другої. Прирівнюючи змішані похідні, маємо

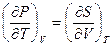(5.14)

і в оберненому вигляді:

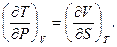(5.15)

Зазначимо, що рівність (5.8), яка визначає вільну енергію 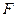, дозволяє інтерпретувати добуток T×S як зв’язану енергію в термодинаміці.

Енергія Гіббса. При незалежних параметрах 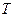і 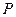термодинамічним потенціалом простої системи, як випливає з (1.12), буде наступна величина, яка називається енергією Гіббса (потенціалом Гіббса):

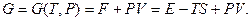(5.16)

Для диференціала 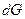з (5.16) та з урахуванням (5.9) маємо:

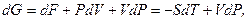(5.17)

звідки, як і в попередніх випадках, знаходимо:

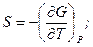
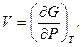(5.18)

Аналогічно результатам (5.12) і (5.13) за допомогою (5.18) отримуємо:

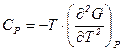(5.19)

і

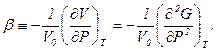(5.20)

Третю пару співвідношень Максвелла знаходимо аналогічно, використовуючи тепер (5.18):

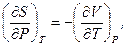(5.21)

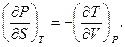(5.22)

Ентальпія. Якщо незалежними параметрами простої системи будуть тиск 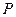і ентропія 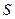, властивості характеристичної функції отримає величина

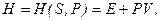(5.23)

яка називається ентальпією. Дійсно, з (5.23) і (5.1) маємо:

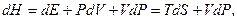(5.24)

звідки

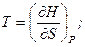
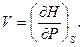(5.25)

З першої рівності (5.25) можна (як приклад) зразу виразити через 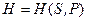теплоємність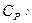

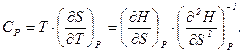(5.26)

З (5.25) отримуємо також останню (четверту) пару співвідношень Максвелла:

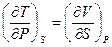(5.27)

і

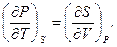(5.28)

Фізичний зміст ентальпії 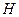виявляється в ізобарних процесах. Тоді при 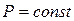з (5.24) маємо:

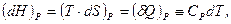(5.29)

звідки видно, що в цьому випадку зміна ентальпії дорівнює кількості теплоти, яка поглинається системою. З цієї причини величину 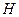часто називають тепловою функцією або тепловмістом. З (5.29) також випливає

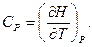(5.30)

Наприкінці підкреслимо, що всі введені тут термодинамічні потенціали (так само, як і внутрішня енергія) є адитивними і однозначними функціями стану. Крім того всі отримані вище формули залишаються справедливими, якщо в них провести узагальнюючу заміну 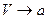і .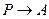

Зв’язок між термодинамічними потенціалами. На підставі (5.8) і другого співвідношення (5.11) можна отримати рівняння

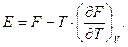(5.31)

Аналогічно з алгебраїчного зв’язку 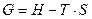і першого співвідношення (5.18) маємо:

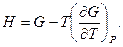(5.32)

Рівності (5.31) і (5.32) називають рівняннями Гіббса-Гельмгольца.

Інтегруючи (5.31) і (5.32), можна знайти 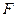або 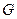відповідно за відомими 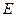і 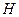. Загальні розв’язки цих диференціальних рівнянь мають вигляд:

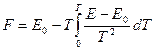(5.33)

і

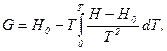(5.34)

де 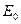і 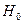– значення відповідних термодинамічних потенціалів при .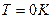