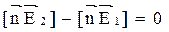Граничные условия

До сих пор предполагалось, что 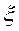, , 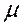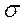являются произвольными функциями tи r. Однако, как правило, они оказываются кусочно- непрерывными функциями претерпевают разрывы на некоторых границах раздела. Обусловлено это тем, что применяемые на практике технические устройства включают в себе элементы, обладающие различными 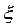, , 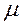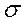.В связи с этим можно получить решение уравнений Максвелла лишь в отдельных областях пространства, где коэффициенты 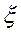, , 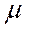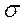непрерывны. Полученное таким образом общее решение системы дифференциальных уравнений содержит некоторые произвольные функции. Чтобы их определить и получить решение для всей совокупности областей, необходимо наложить граничные условия, или, как говорят «сшить» решения на границах областей. 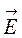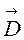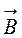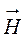Эти условия «сшивания», налагаемые на векторы , , и можно вывести, используя интегральную форму уравнений Максвелла. В самом деле, применять в пограничной области уравнения в дифференциальной форме нельзя, так как поля на границе могут терпеть разрывы, поэтому пространственные производные от них могут не существовать.

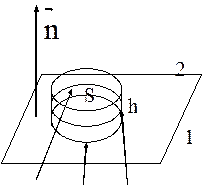Найдем граничные условия для 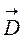на границе двух сред. В качестве объема V возьмем бесконечно малый цилиндр с основанием S и высотой h, верхний и нижний торцы которого лежат соответственно в диэлектриках 2 и 1 (рис.). Так как цилиндр мал, то уравнение

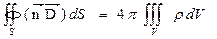
При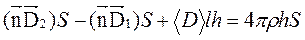

где n-нормаль к поверхности раздела, l- длина окружности основания, <D>- среднее значение нормальной к боковой поверхности составляющей D. Пусть 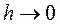при фиксированном S. При вычислении предела учтем, что поле D всюду ограничено, так что слагаемое 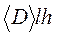исчезает. В пограничной области могут существовать большие скопления заряда, что даже в пределе 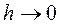заряд внутри цилиндра на элементе 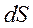граничной поверхности может быть отличным от нуля и равным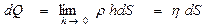

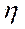- поверхностная плотность электрического заряда. Окончательно при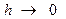

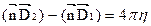При наличии поверхностного заряда по границе двух сред нормальная составляющая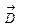изменяется на границе скачком на 4 .

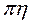Аналогично получаются граничные условия и для вектора магнитной индукции В. Согласно из3 уравнений Максвелла 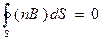откуда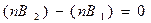

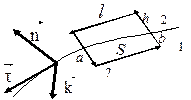т. е. нормальная составляющая вектора магнитной индукции не имеет разрыва на поверхности раздела двух магнетиков.

Применив первое из интегральных уравнений Максвелла к контуру С, получающемуся при рассечении цилиндра (рис.) вдоль нормали n:

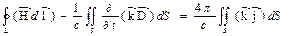
где 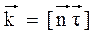; 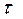- единичный вектор, касательный к поверхности раздела. Пусть теперь 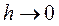при малом фиксированном l. Тогда

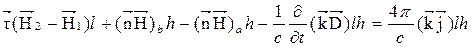
Примем во внимание конечность 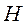и 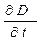, а так же, что в пограничной области могут протекать столь большие токи, что даже в пределе 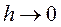сила тока, протекающего сквозь контур C на участке 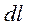поверхности раздела, может быть отлична от нуля и равна

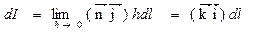Вектор i называется в таких случаях поверхностной плотностью тока. В результате имеем 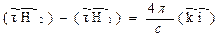(15.1)

Подставив в (15. 1) 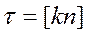, найдем, ввиду произвольной ориентации k в касательной плоскости, 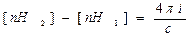Таким образом, касательная проекция [nH] вектора напряженности магнитного поля непрерывна на границе раздела двух сред, если отсутствует поверхностный ток проводимости. При наличии же после6днего она испытывает на границе раздела скачок, равный 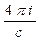.Граничное условие для тангенциальной составляющей вектора напряженности электрического поля имеет вид: