Холодильные установки и тепловые насосы

Холодильные установки предназначены для поддержания в ее камере температуры ниже температуры окружающей среды. Если в камеру помещают предметы (продукты), температура которых превышает установленную температуру в камере, для их охлаждения необходимо отбирать от них теплоту и выбрасывать ее в окружающую среду. Из 2-го закона термодинамики известно, что самопроизвольно теплота переходит от более нагретых к менее нагретым телам (например, через теплоизоляцию стенок холодильника от окружающей среды внутрь камеры). Для того, чтобы передать теплоту на более высокий температурный уровень, нужно затратить работу. Теоретически такая возможность вытекает из обратного цикла Карно abcd (рис. 6.11).

Рис. 6.11 Обратный цикл Карно в Ts - диаграмме

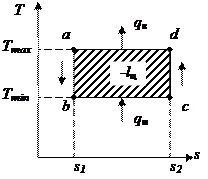
В процессе адиабатного расширения ab температура рабочего тела уменьшается от Т_max до Т_min. В процессе bc оно при постоянной температуре Т_min расширяется, забирая теплоту q_н из холодильника (в термодинамике говорят «от низкотемпературного источника») в Ts диаграмме эта теплота изображена площадью s₁dcs₂. В процессе cd рабочее тело подвергается адиабатному сжатию, в результате чего его температура повышается от Т_min.до Т_max. Наконец, после изотермического сжатия da при температуре Т_max рабочее тело возвращается в исходное состояние а, отдавая в процессе da теплоту q_в в окружающую среду («высокотемпературному источнику»). Эта теплота изображается в Ts-диаграмме площадью s₁ads₂, в работа l_ц, затраченная на перенос теплоты с низшего температурного уровня Т_min на более высокий T_max (эквивалентная соответствующей теплоте) – площадью цикла abcd. Количество теплоты, отобранной из камеры холодильника (в данном случае за цикл – площадь s₁dcs₂), называется холодопроизводительностью. Эффективность холодильного цикла выражается холодильным коэффициентом e_х – отношением холодопроизводительности к затраченной на осуществление цикла работе. В обратном цикле Карно

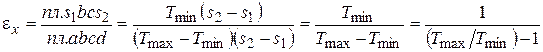. (6.7)

Их формулы (6.7) видно, что эффективность холодильной машины тем больше, чем меньше отношение абсолютных температур окружающей среды и в холодильной камере. Жарким летом холодильник, установленный в комнате, работает менее эффективно (потребляет больше электроэнергии), чем зимой, когда в комнате холоднее.

По ряду причин цикл Карно в холодильной технике не применяется. Холодильные машины строят на основе других циклов – менее эффективных с точки зрения термодинамики, но более экономичных практически.

Тепловым насосом называется устройство, которое передает теплоту более низкого потенциала на более высокий потенциал за счет затрат энергии еще более высокого потенциала. По принципу действия – это та же холодильная машина, но ее полезным эффектом является передача теплоты q_н, взятой у холодного источника вместе с затраченной на это энергией l_ц, не в окружающую среду, как в холодильном цикле, а тепловому потребителю, имеющему более высокую температуру. Если, например, имеем в пруду летом воду с температурой 20°С, а для горячего водоснабжения нужна вода с температурой 65°С, то с помощью теплового насоса можно использовать прудовую воду для горячего водоснабжения. Это значительно выгоднее, чем просто нагревать воду от 20°С до 65°С электричеством.

Простейшим и теоретически наиболее эффективным циклом теплового насоса является тот же обратный цикл Карно (рис. 6.11). Работа теплового насоса характеризуется коэффициентом преобразования энергии (КПЭ), под которым понимается отношение количества теплоты q_в, отданной потребителю, к количеству потребленной механической энергии l_ц

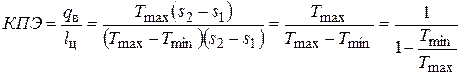. (6.8)

Из формулы (6.8) видно, что КПЭ увеличивается с увеличением отношения Т_min/Т_max. Чем ближе температура низкотемпературного источника Т_min к необходимой температуре теплоносителя, (например, горячей воды в системе гвс) Т_max, тем больше эффекта от применения теплового насоса. При Т_min=273+20=293 К и Т_max=273+65=338 К КПЭ=1/(1–(293/338))=7,5. Это значит, что на нагрев теплоносителя (например, воды) от 20°С до 65°С в идеальном тепловом насосе нужно затратить в 7,5 раз меньше электроэнергии, чем при прямом нагреве воды электричеством.

На прямой электронагрев одного килограмма воды от 20°С до 65°С (dt=45°С) пришлось бы затратить q_нагр=cdt=4,187×45=188 кДж/кг электроэнергии (здесь с – теплоемкость воды). В тепловом насосе, осуществленному по обратному циклу Карно, для этого потребуется всего 188/7,5=25 кДж/кг.

Практически в тепловых насосах как и в холодильных машинах, применяется не обратный цикл Карно, а другие циклы, более приемлемые с инженерной точки зрения. Их КПЭ грубо составляет примерно 0,5-0,6 в зависимости от мощности) от КПЭ обратного цикла Карно.

Контрольные вопросы и задачи

6.1. Вывести формулу для КПД цикла ДВС со сгоранием при р=const и сравнить КПД двух циклов при одинаковых значениях e; v₇/v₂ (см. рис. 6.3) обозначить через r. К какому значению стремится h_t при r®1?

6.2. Почему вырабатываемая газовой турбиной мощность превышает мощность, затраченную на привод компрессора, если массовые расходы через них рабочего тела и перепады давления практически одинаковы см. рис. 6.5)?

6.3. Пользуясь h, s – диаграммой водяного пара, посчитать КПД цикла Ренкина на насыщенном паре при давлении перед турбиной 9,8 МПа. Сравнить с КПД цикла Карно, имеющего те же параметры, а также цикла Ренкина при перегреве пара до 540°С. Давление за турбиной 4 кПа.

6.4. Имеет ли смысл поставить холодильник, чтобы снизить температуру конденсации пара за турбиной и тем самым повысить КПД цикла?

Решения задач и ответы на вопросы

1.1. Можно.

1.2. Температура не изменится.

1.3. В стационарном неравновесном состоянии.

2.1. 18,6 мин.

2.2.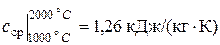

2.3. Не надо, так как DU=14380 кДж, а L=5 кДж.

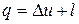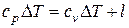2.4. Согласно первому закону термодинамики подведенная теплота или , откуда

.

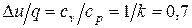4.1. Кажущаяся молекулярная масса смеси

.

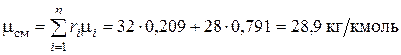Плотность воздуха при нормальных физических условиях

.

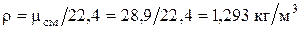Состав воздуха по массе

;

.

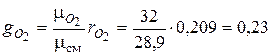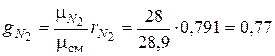Парциальные давления кислорода и азота

;

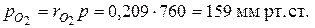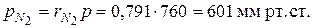
4.2. Начальный объем воздуха

.

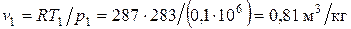Из уравнения процесса конечный объем

.

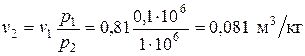Работа, затрачиваемая на сжатие,

.

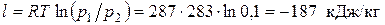Количество теплоты, отводимой от газа, равно работе сжатия, поэтому q= – 187 кДж/кг.

4.3. Чтобы найти изменение температуры, рассмотрим столб воздуха, высотой dy с поперечным сечением, равным единице. На нижней поверхности этого столба давление равно р, а на верхней оно составляет р+dp, где dp – изменение давления, вызванное весом столба воздуха. Поскольку увеличение высоты сопровождается уменьшением давления, то 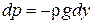. Так как 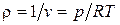, то 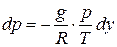. Для адиабатного процесса 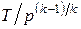=сonst. Логарифмирование и дифференцирование этого уравнения дает

.

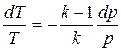После подстановки выражения для dp, получаем

.

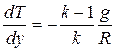Полагая k=1,4; R=287 Дж;/(кг×К); g=9,81 м/с², получаем

.

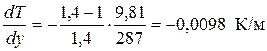Наблюдаемое в действительности среднее снижение температуры по высоте (1 К на каждые 200 м) несколько меньше вычисленного. Различие объясняется неучетом влажности воздуха. Когда при некоторой температуре воздух окажется насыщенным влагой, то дальнейшее понижение температуры приведет к конденсации водяных паров и выделению теплоты конденсации. По этой причине понижение температуры будет происходить медленнее, чем это следует из расчета.

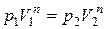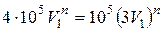4.4. В политропном процессе или , откуда показатель политропы расширения .

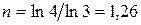Работа расширения

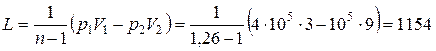кДж.

Количество теплоты 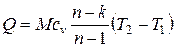, но 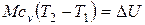- изменение внутренней энергии газа, которое по первому закону термодинамики равно DU=Q – L, поэтому

,

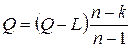откуда

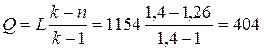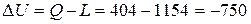кДж;

кДж.

Работа расширения совершается газом за счет сообщения ему теплоты и уменьшения его внутренней энергии.

4.5. По h, s – диаграмме находим, что пар в конце расширения будет влажным со степенью сухости х=0,81.Начальные параметры: h₁=3405 кДж/кг; v₁=12,7 м³/кг.

Изменение внутренней энергии

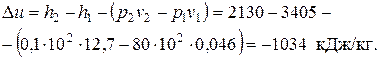
5.1. Абсолютное давление воздуха в воздухопроводе

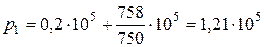Па.

Отношение давлений при истечении

,

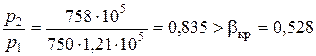поэтому скорость истечения меньше критической и определяется по формуле

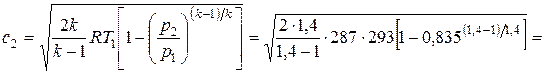183 м/с.

Удельный объем воздуха в воздухопроводе 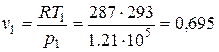м³/кг. Площадь отверстия 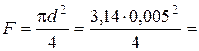19,6×10^-6 м².

Секундный расход найдем по формуле

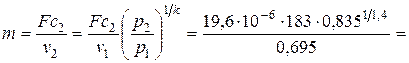5,17×10^-3 кг/с.

5.2.

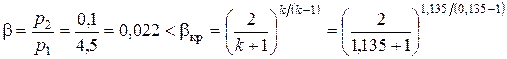=0,577.

Следовательно, истечение происходит в сверхзвуковой области.

Критическое давление р_кр=b_крр₁=0,577×4,5=2,6 МПа.

Скорость истечения из суживающегося сопла

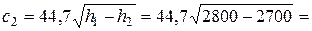44,7 м/с;

то же из сопла Лаваля

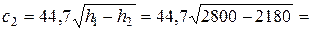1113 м/с.

Таким образом, при замене суживающегося сопла соплом Лаваля скорость истечения увеличится в 2,5 раза.

5.3. За счет неравновесности процесса дросселирования.

5.4. Да, можно, если начальное давления дросселируемого пара больше 2,9 МПа.

5.5.

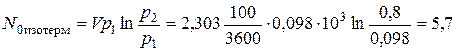кВт.

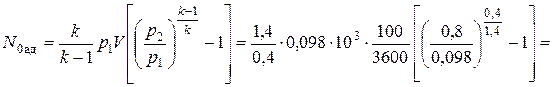7,7кВт.

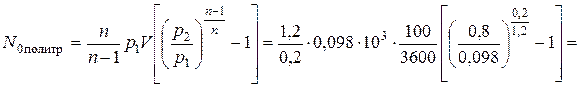6,8кВт.

6.1. ; так как r > 1 и k>1, то 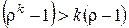. Значит, чем больше r, тем бóльшая величина вычитается из единицы, т .е. меньше h_t. При r®1, раскрывая неопределенность, получим h_t® .

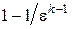6.2. Температура газа в турбине, чем в компрессоре поэтому больше и удельный объем при том же давлении, а элементарная техническая работа 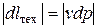. В результате и 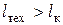(см. рис. 6.6).

6.3. Температура насыщения при р=0,8 МПа равна 309°С, а при р = 4×10^-3 МПа - 29°C. КПД цикла Карно в этом диапазоне температур равен 0,48. КПД циклов Ренкина – 0,4 и 0,43.

6.4. Теплообменник нужно ставить после конденсатного насоса, так как до него вода находится при температуре кипения; подогреть ее, не превращая в пар, при этом давлении нельзя. КПД цикла повысится за счет регенерации теплоты – меньше теплоты отработавшего пара будет отдано холодному источнику в конденсаторе.

Приложение 1

Таблица П.1.

Термодинамические свойства воды и водяного пара в состоянии насыщения (по температуре)