Рух електрона в періодичному полі

Кристалічної решітки

21.1 Мета роботи

Вивчити природу виникнення зонної структури енергетичного спектра електрона в кристалі та дослідити залежність ефективної маси електрона від його розташування в енергетичній зоні.

21.2 Вказівки з організації самостійної роботи

Розглянемо найпростіший приклад одновимірного періодичного поля, який дозволяє отримати точний розв’язок задачі. Незважаючи на схематичність моделі кристала, цей приклад чітко показує природу виникнення зонної структури енергетичного спектра електрона. Припустимо, електрон рухається в одновимірному полі, зображеному на рис.21.1.

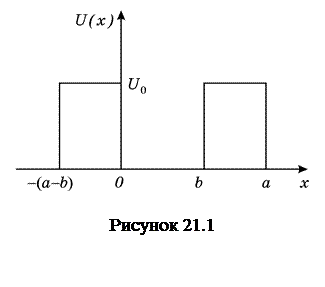В цьому випадку розв’язок рівняння Шредінгера в областях, де потенціальна енергія дорівнює нулю, матиме такий вигляд:

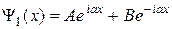, (21.1)

де – хвильове число вільного електрона;

m – маса електрона;

Е – його повна енергія;

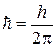– стала Планка.

В областях, які відповідають бар’єрам,

, (21.2)

де 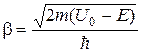– хвильове число в області бар’єра.

Граничні умови для 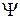-функції та ії похідних на межах +b, 0, –(a–b) запишемо у такому вигляді:

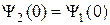, , (21.3)

та

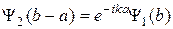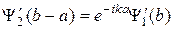, , (21.4)

де k – дійсна величина.

У співвідношеннях (21.4) ми скористались загальними властивостями хвильових функцій електрона в періодичному полі .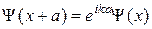

Підставляючи розв’язок рівняння Шредінгера (21.1), (21.2) в граничні умови (21.3) і (21.4), отримуємо рівняння для визначення невідомих сталих
A, B, C, D, k:

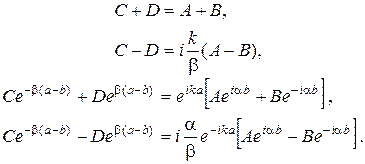(21.5)

Сумісний розв’язок системи рівнянь (21.5) можливий, якщо її детермінант дорівнює нулю, тобто якщо:

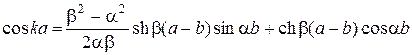. (21.6)

Розв’язуючи рівняння (21.6) графічним способом, можна визначити енергетичний спектр електрона. З метою спрощення задачі перейдемо у виразі потенціальної функції (рис.21.1) до спрощення виразу, покладаючи 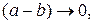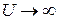. При цьому переході величина

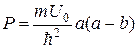(21.7)

пропорціональна площі бар’єра і залишається скінченною. Тоді, зважаючи на те, що в цьому наближенні 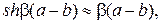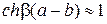, замість (21.6) отримуємо рівняння

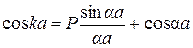. (21.8)

Внаслідок того, що величина k – дійсна, це рівняння (21.8) задовольняєть­ся у випадку, коли його права частина залишається в межах від –1 до +1.

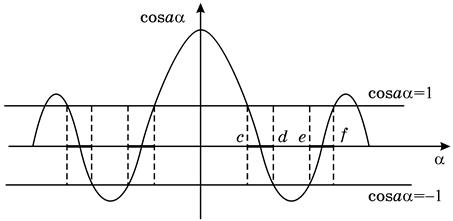
Рисунок 21.2

Значення , які задовольняють рівняння (21.8) знаходяться в межах с–d, e–f. В проміжку d–e коренів немає, бо права частина виразу (21.8) за модулем більше одиниці. Цим значенням відповідатимуть значення 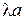, межі яких визначаються нерівністю: .

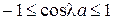Отже, енергетичний спектр електрона матиме зонну структуру: значеням k, які належать проміжкам c–d, e–f відповідають значенням енергії, які утворюють дозволені зони. В проміжку d–e корені відсутні – він відповідає забороненій зоні. Межам першої (по порядку) зонн – с–d відповідають значення 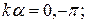другої: 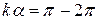і т.п.

Динаміку електрона в кристалічний решітці можна описати за допомогою другого закона Ньютона

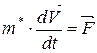, (21.9)

де 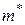– ефективна маса електрона

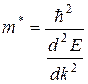. (21.10)

Вона формально відіграє роль маси по відношенню до зовнішньої сили 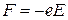, яка діє з боку зовнішнього поля напруженістю Е.

Ефективна маса може дуже відрізнятися від фактичної маси електрона m. Це обумовлено тим, що в дійсності рівняння другого закону Ньютона для електронів в кристалі має вигляд

,

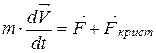де – сила, обумовлена дією на електрон поля решітки.

Введення ефективної маси дозволяє, абстрагуючись від взаємодії електрона з решіткою, визначати характер руху електрона під дією зовнішнього поля. Приписуючи електрону масу m^* можна вивчати поведінку електрона під дією сили 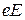, вважаючи його вільним.

Ефективну масу в даній роботі поблизу “дна” та “стелі” зони можна обчислити за формулою

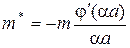, (21.11)

де через 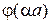позначено праву частину рівняння (21.8), 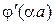– її похідна за змінною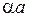

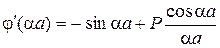. (21.12)

21.3 Опис комп’ютерної програми

Зовнішній вигляд інтерфейсу програми зображено на рис. 21.3. Алгоритм програми обчислень в даній роботі базується на рівнянні (21.8). Програма будує графіки лівої та правої частини рівняння, точки перетину яких дають корені рівняння. Змінюючи параметри задачі, можна отримати всі можливі випадки спектра власних значень хвильового числа та енергії електрона, що рухається в періодичному полі кристала: безперервного, квазі-безперервного (тобто, спостерігати важливий момент – появу енергетичних зон в кристалі) та дискретного, коли висота бар’єра сягає таких значень, що електрон стає “запертим” в “глибокій” потенціальній ямі. Програма дозволяє також шляхом підведення курсора “мишки” в будь-яку точку графіка, отримати значення ефективної маси електрона в залежності від його “положення”: поблизу “дна”, поблизу “стелі” та всередині дозволеної зони.

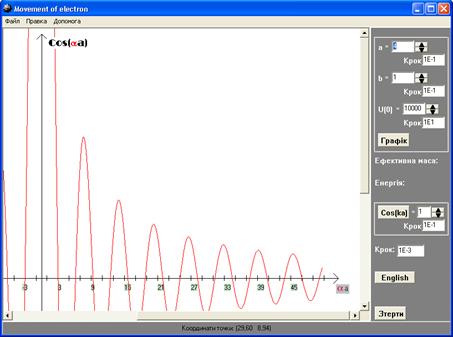
Рисунок 21.3

21.4 Інструкція користувачу

1. Занести значення параметрів 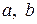(в ангстремах), U – в електрон-вольтах у відповідності з табл. 21.1 завдань. Отримати на екрані графік лівої та правої частини рівняння (21.6).

2. Записати значення , які відповідають межам дозволених зон (по горизонтальній осі відкладені значення ).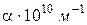

3. Відкласти отримані значення на горизонтальній осі та позначити жирною лінією дозволені зони. Зробити висновок, як поводять себе ширина дозволеної та ширина забороненої зони зі збільшенням хвильового числа ?

4. Збільшуючи величину (при незмінних значеннях 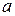та 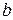) здобути звуження дозволених зон практично до нуля. Записати значення , визначити відповідне значення енергії

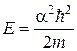(21.13)

та порівняти з відповідними значеннями енергії електрона, який знаходиться в нескінченно глибокій ямі шириною .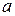

5. Поступово зменшувати величину (від початкової величини пункту 2) доти, доки не залишиться лише одна зона. Записати для п’яти 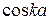відповідні значення . Обчислити відповідні значення енергії за формулою (21.13). Побудувати залежність 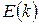. Зробити висновок, де будуть густіше розташовані рівні енергії: поблизу “дна” або “стелі” зони чи в середині зони?

Таблиця 21.1 – Вихідні дані

Номер вар.	a·10-10, м	b·10-10, м	U, eB	Номер вар.	a·10-10, м	b·10-10, м	U, eB
		3,9				1,9
		3,5			3,5	3,3
					4,5	4,2
						4,8
		4,5				2,5
		2,9			2,5	2,2

6. Зменшуючи подалі висоту бар’єрів , отримати зникнення зон. Яким буде спектр електрона в цьому випадку?

7. Обчислити значення ефективної маси біля “дна“ та “стелі” першої енергетичної зони за даними пункту 6. Зробити висновки.

21.5 Зміст звіту

Звіт має містити: мету роботи, результати виконання роботи, а саме:

1) схему дозволених та заборонених зон;

2) порівняльну таблицю значень енергії, обчислених за результатами обчислення на ПК величини зі значеннями енергії для ями з нескінченно високими стінками тієї самої ширини а ( );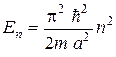

3) значення ефективної маси відповідно в середині, поблизу “дна”, та “стелі” дозволеної зони;

4) графік залежності ;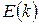

5) висновки щодо спектра значень енергії в даній структурі взагалі, в середині дозволеної зони, для значень , коли зони зникають, а також у випадку, коли .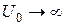

21.6 Контрольні запитання і завдання

1. Яка фізична модель кристала покладена в основу даної роботи?

2. Який вигляд мають 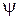-функції між бар’єрами та в самих бар’єрах?

3. Запишіть граничні умови, яким має задовольняти 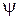-функція та її похідна.

4. Що таке “ефективна маса” електрона?

5. Яким методом розв’язується рівняння для властивих значень сталої розповсюдження (хвильового числа)?

6. Що таке “дозволена зона”, “заборонена зона”?

7. Як поводить себе ефективна маса електрона біля “дна”, в середині та біля “стелі” дозволеної зони?