Волновые процессы
Если на каком-либо участке сплошной упругой среды возбудить гармоническое колебание, то оно будет передаваться соседним участкам этой среды, от них в свою очередь другим участкам и т.д. Такой процесс называется волновым.
Различают поперечные и продольныеволны. Волна называется поперечной, если частицы среды колеблются перпендикулярно направлению ее распространения, и продольной, если они колеблются вдоль этого направления. Продольные волны могут распространяться в твердых, жидких и газообразных телах. Поперечные волны распространяются лишь в твердых телах. Примером поперечных волн являются волны, возбуждаемые при колебаниях струны, примером продольных - звуковые волны. Важно отметить, что сами частицы среды не переносятся волной, они лишь колеблются около положения равновесия.
Рис. 1.10
Наименьшее расстояние между двумя частицами, колеблющимися в одинаковой фазе, называется длиной волны λ (см. Рис. 1.10). λ - расстояние, на которое распространяется волна за время, равное периоду Т, т.е.
λ = VТ, (1.25)
где V-скорость волны.
Скорость распространения волны определяется упругими свойствами среды и ее плотностью ρ:
а) для продольных волн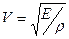 
, где Е-модуль Юнга.
б) для поперечных волн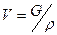 
, где G-модуль сдвига.
Уравнение бегущей волны. Бегущей называется волна, которая переносит энергию. Перенос энергии характеризуется вектором плотности потока энергии – вектором Умова:
.
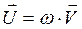Здесь ω - объемная плотность энергии волны, энергия переносимая волной за 1с через 1м2 площадки, перпендикулярной лучу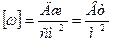 
.
Представим себе волну, создаваемую источником в точке у=0, колеблющимся по закону х=А соs ωt и распространяющуюся вдоль оси у (Рис.1.10).
Обозначим время, в течение, которого колебания среды достигнут любой произвольной точки у через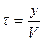 
. Колебания этой точки будут гармоническими, но они отстают от колебаний точки у = 0 на время τ:
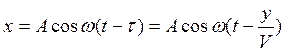, (1.26)
где V-фазовая скорость (скорость распространения колебаний в среде).
Уравнение (1.26) будет уравнением плоской бегущей волны.
Учитывая, что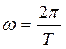 
и ТV=λ, это уравнение можно переписать:
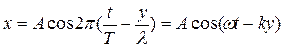, (1.27)
где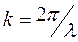 
- волновое число.
В общем случае уравнение плоской монохроматической волны, распространяющейся вдоль оси у, будет:
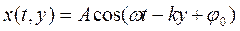, (1.28)
где φ0-начальная фаза колебаний.
Для двух точек волны, лежащих на расстоянии Δу друг от друга разность фаз будет:
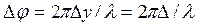, (1.29)
где Δ=Δу - разность хода волн.
Если Δу=λ, то точки колеблются с разностью фаз Δφ=2π.
Если Δу= λ/2, то разность фаз Δφ= π (точки колеблются в противофазе).