Інверсна населеність рівнів

ЛАБОРАТОРНА РОБОТА № 7

ВИВЧЕННЯ ГЕЛІЙ-НЕОНОВОГО ЛАЗЕРА І ВИЗНАЧЕННЯ ДОВЖИНИ ХВИЛІ ВИПРОМІНЮВАННЯ ЛАЗЕРА ЛГ-44

Мета: Вивчити будову і принцип роботи гелій-неонового лазера та визначити довжину хвилі випромінювання лазера ЛГ-44.

Прилади та матеріали:Гелій-неонові лазери: ЛГ-31, ЛГ-44, диф­ракційна решітка (d = 0,01 мм) , набір по поляризації світла, екран пере­носний, вимірювальна лінійка.

Теоретичні відомості та опис приладів

Оптичні квантові генератори (лазери), які з’явилися на початку 60-х років, отримали широке поширення як джерела випромінювання, що працюють в оптичному діапазоні частот. Термін “лазер” утворений із початкових букв англійського словосполучення – “підсилення світлових коливань за допомо­гою індукованого випромінювання”. Великий прогрес в області квантової електроніки зумовлений позитивними якостями лазерного випромінювання, яке володіє високою часовою і просторовою когерентністю, монохроматичністю і напрямленістю. Можливість ефективного його фокусування дозволяє отримати надзвичайно велику густину енергії в світловому пучку. Ці можливості лазерів мають істотне значення для розвитку таких галузей радіотехніки як локація, навігація, зв’язок, телебачення, обчислювальна техніка тощо. Відоме також технічне застосування лазерів.

Спонтанне і вимушене випромінювання коливань

В основі роботи лазера лежать три фундаментальні явища, які мають місце при взаємодії електромагнітних хвиль з речовиною, зокрема процеси спонтан­ного і вимушеного випромінювання та погли­нання.

Спонтанне випромінювання

Розглянемо у деякому середовищі два енергетичні рівні 1 і 2 з енергіями Е1­­ і Е₂(Е₁< Е₂) . При дальшому розгляді це можуть бути будь-які два рівні з необмеженого набору рівнів, властивих даному середовищу. Однак зручно прийняти рівень 1 за основний. Припустимо, що атом (або молекула) речовини знаходиться в початковому стані, який відповідає рівню 2. Оскільки E₂> E₁, атом буде намагатися перейти на рівень 1. Отже з атома повинна виділитись енергія, яка рівна різниці енергій E₂– E₁. Коли ця енергія звільниться у вигляді електромагнітної хвилі самовільно, то цей процес називають спонтанним (самовільним) випроміню-ванням. При цьому частота випроміненої хвилі визначається за формулою (отриманої Планком)

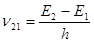, (16.1)

де h – стала Планка. Таким чином, спонтанне випромінювання характери­зується випромінюванням фотона з енергією

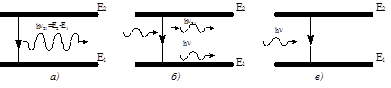Рис. 16.1

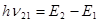, (16.2)

при переході атома з рівня 2 на рівень 1 (рис 16.1, а).

Характерною особливістю спонтанних переходів є те, що вони не пов’язані з впливом яких-небуть зовнішніх змінних полів на атомну систему. Причиною спонтанних переходів є внутрішні збурення, флуктуації в квантових системах, природа яких ще достатньо не розкрита. При спонтанному випромінюванні окремі атоми випромінюють незалежно один від одного, і окремі акти випро­мінювання не зв’язані в часі, тому поляризація і напрямок випромінювання електромагнітних хвиль можуть бути будь-якими. Звідси випливає висновок – спонтанне випромінювання по відношенню до зовнішнього поля буде не когерентним, шумовим, ненапрямленим.

Імовірність спонтанного випромінювання можна визначити слідуючим чином. Припустимо, що в момент часу t на рівні 2 знаходиться N₂атомів (в одиниці об‘єму). Швидкість переходу 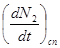цих атомів внаслідок спон­танного випромінювання на нижній рівень, очевидно пропорційна N₂. Значить можна записати, що

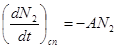, (16.3)

де А – характеризує імовірність спонтанного випромінювання і називається коефіцієнтом Ейнштейна. (Вираз для А вперше був отриманий Ейнштей­ном із термодинамічних міркувань). Величину t_cn=1/A називають спонтанним часом життя. Чисельні значення величин А і t_спзалежать від конкретного переходу, який бере участь у випромінюванні.

1.2. Вимушенне випромінювання

Припустимо знову, що атом в початковому стані знаходиться на верхньому рівні 2 і на речовину падає електромагнітна хвиля з частотою, яка визначається виразом (13.1). Окільки частоти падаючої хвилі і випромінювання, зв’язаного з атомним переходом, рівні одна одній, то існує скінченна імовірність того, що падаюча хвиля викличе перехід атома з рівня 2 на рівень 1 (2®1) (рис 16.1, б) . При цьому різниця енергій Е2 – Е1виділиться у вигляді електромагніт­ної хвилі, яка додається до падаючої. Це і є явищевимушеного випро-мінювання. Його ще називають індукованимабо стимульованим випромінюванням.

Існує важлива особливість вимушеного випромінювання: вторинний фотон, який виникає в результаті переходу, не відріз-няється від того фотона, який стимулював цей перехід. Обидва фотони характеризуються однаковими параметрами: при вимуше-ному випромінюванні частота, напрямок поширення і стан поляризації індукованого випромінювання точно співпадають з частотою, напрямком поширення і поляризацією довільного електромагнітного поля, яке викликало це випромінювання і співфазні з ним, тобто фази вимушуючих і випромінених квантів жорстко зв’язані. Звідси випливає, що оскільки первинні і вторинні фотони невіддільні то зрозуміло, що таке випромінювання набуває властивостей монохроматичності, когерентності і напрямленості.

Процес вимушеного випромінювання також можна описати за допомогою рівняння:

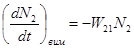, (16.4)

де (dN₂/dt)_вим– швидкість переходу 2®1 за рахунок вимушеного випроміню­вання, W₂₁– імовірність вимушеного переходу. Як і коефіцієнт А у виразі (16.3), величина W₂₁також має розмірність (час)^-1. Однак, на відміну від А імовірність W₂₁залежить не тільки від конкретного переходу, але й від інтенсивності падаючої електромагнітної хвилі, оскільки вимушене випромінювання може відбуватися тільки під дією зовнішнього поля. Точніше, для плоскої хвилі:

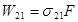, (16.5)

де F – густина потоку фотонів в падаючій хвилі, s₂₁– переріз вимушеного випромінювання. Ця величина має розмірність площі і залежить лише від характеристик даного переходу.

1.3. Поглинання

Припустимо зараз, що атом в початковому стані знаходиться на рівні 1. Якщо це основний рівень, то атом буде залишатися на ньому до тих пір, поки на нього не подіє якесь зовнішнє збурення. Нехай на речовину падає електро­магнітна хвиля з частотою n, яка визначається формулою (16.1). В такому разі існує скінченна імовірність того, що електрон перейде на верхній рівень 2. Різниця енергій Е₂– Е₁, яка необхідна для того, щоб атом здійснив перехід, береться із енергії електромагнітної хвилі. В цьому заключається суть процесу резонансного поглинання.

За аналогією з (16.4) імовірність поглинання W₁₂визначається рівнянням:

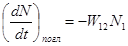, (16.6)

де N₁– число атомів в одиниці об‘єму, які в даний момент часу знаходяться на рівні 1. Крім того, подібно до виразу (16.5) можна записати

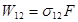, (13.7)

де s₁₂– деяка характерна площа (переріз поглининня), яка залежить лише від конкретного переходу.

Принцип роботи лазера

Інверсна населеність рівнів

Рис. 16.2

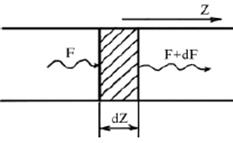
Розлянемо в якомусь середовищі енергетичні рівні 1 і 2 з відповід­ними населенностями N₁і N₂. Нехай в цьому середовищі в напрямку осі Z поши­рюється плоска хвиля з інтенсивністю, яка відповідає густині потоку фотонів F.

Тоді, відповідно виразів (16.4) – (16.7), зміна густини потоку dF, яка обумовлена як процесами випроміню­вання, так і процесами поглинання, в шарі dZ (заштрихована область на рис. 16.2) , визначається рівнянням

dF = s F (N₂– N₁) dZ. (16.8)

Із рівняння (16.8) випливає, що у випадку N₂> N₁средовище веде себе, якпідсилювач(тобто dF/dZ > 0), а у випадку N₂< N₁– як поглинач. Відомо, що при термодинамічній рівновазі насе­леності енергетичних рівнів описуються статис­тикою Больцмана. Так, якщо 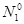і 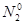– населеності двох рівнів при термо­динамічній рівновазі, то маємо:

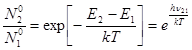(16.9)

де k – стала Больцмана, Т – абсолютна температура середовища.

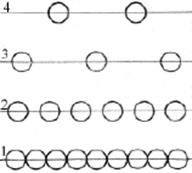Рис. 16.3

Звідси видно, що при низьких температурах, коли (Е₁– Е₂)/(kТ) >> 1 (випадок теплової рівноваги), виконується нерівність N₁>> N₂і основна час­тина атомів знаходиться у незбудженому стані з енергією Е₁(рис. 16.3). У відповідності з (16.8) середовище поглинає випромінювання на частоті n, що як правило спостерігається на практиці. Однак, якщо вдастся досягнути нерівноваж-ного стану, для якого , то сере­довище буде діяти, як підсилювач. В цьому випадку говорять, що в середовищі існує, інверсія*населе­ностей, маючи на увазі, що різниця населеностей (N₂– N₁> 0) протилежна за знаком тій, яка існує у звичайних умовах (N₂⁰– N₁⁰< 0).

Середовище, в якому здійснюється інверсія насе­леностей, називають активним середовищем.

В дворівневій системі інверсія населеностей енергетичних рівнів може бути описана за допомогою поняття від’ємної абсолютної температури. Припустимо, що відношення (16.9) містить визначення абсолютної температури і описує не тільки рівно­важний стан із населеністю N₁⁰і N₂⁰, але і рівноважні стани з населеностями N₁і N₂. Тоді

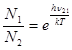, (16.10)

звідси

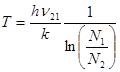. (16.11)

Із (16.11) випливає, що при N₁> N₂, коли більшість атомів знаходяться в незбудженому стані, ln (N₁/N₂) > 0 і абсолютна температура Т додатна. При N₁=N₂, коли населеності рівнів Е₁і Е₂однакові, ln (N₁/N₂) = 0 і абсолютна температура перетворюється в нескінченість. При N₁< N₂, коли більшість атомів знаходять­ся в збудженому стані, ln (N₁/N₂) < 0 і абсолютна температура від‘єм­на.

Таким чином, від‘ємна температура є характеристикою нерівноваж­ного стану.

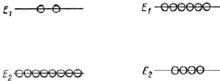а б

Рис. 16.4

Привести середови­ще у стан інверсної населеності можна під дією енергетичних впли­вів – підвищення темпе­ратури, освітлення, бом­барду­вання швидкими частинками тощо. На рис. 16.4 наведена нормальна (рис 16.4, а) і інверсна (рис 16.4, б) населеності енергетичних рівнів.

2.2 Умови, необхiднi для створення у середовищi iнверсної населеностi рiвнiв

Експерименти показали, що не в будь-якому середовищi можна створити стан з iнверсною населенiстю рiвнiв. Наприклад, створити iнверсну населенiсть в системi з 2-х рiвнiв (дворiвнева населенiсть) навiть шляхом тривалого освiтлення речовини потужним свiтловим iмпульсом неможли­во. Це пов’язано iз слiдуючими причинами: по-перше, iз збiльшенням концентрацiї частинок на верхньому рiвнi (рівні з енергiїю Е₂), зростає імовірність спонтанних переходів; по-друге, збуджуюче випромінювання викликає вимушене випромінювання, яке переводить частинки на нижній рівень.

Інші можливості відкриваються при використанні системи з трьома рівнями, серед яких є такі збуджені стани, в яких атоми можуть знаходитись не 10^-8с, а значно триваліше. Такі стани і рівні енергій, які їм відповідають називають метастабільними.

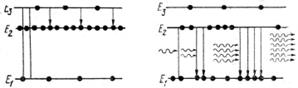а б

Рис. 16.5

Нехай рівень енергії Е₂(рис. 16.5, а) метастабільний і характеризу­ється “часом життя” в 1000 разів більшим за “час життя “рівня Е₃(t~10^-8с).

При наявності рівня Е₂можливі спонтанні переходи із стану Е₃не тільки в основний стан Е₁, але й переходи на метастабільний рівень Е₂. Обидва переходи супроводжуються виділенням відповідної енергії:

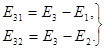(16.12)

Велика різниця в тривалостях життя в станах Е₃і Е₂призводить до того, що під дією збуджуючих фотонів з енергією hn ³ Е₃– Е₁атоми переходять спочатку у стан Е₃, а потім вип­ро­мі­нюючи квант з енергією Е₃₂= Е₃– Е₂, вони переходять в стан Е₂. В результаті відбувається накопичення атомів на метастабільному рівні Е₂і число їх з часом виявляється більшим за число атомів на основному рівні Е₁. Значить, в результаті з такою системою рівнів під дією збуджуючого випроміню­вання hn ³ Е₃– Е₁може бути створена інверсна населеність рівнів.

Якщо направити в попередньо підготовлену таким чином речовину квант електромагнітного випромінювання hn₂₁= Е₂– Е₁, то внаслідок явища інду­кованого випромінювання відбудеться підсилення світла, що умовно показано на рис 16.5, б. Число випромінених фотонів збільшується в геометричній прогресії. На виході підсилювача світла фотонів більше, ніж на вході, або, що теж саме, амплітуда електромагнітних коливань зростає пропорційно числу індукованих переходів.

Система атомів з інверсною населеністю рівнів здатна не тільки підсилю­вати, але й генерувати електромагнітне випромінювання. Для роботи в режимі генератора необхідний додатковий зворотний зв’язок, при якому частина сигналу з виходу пристрою подається на його вхід. Для цього активне середовище, в якому створюється інверсна населеність рівнів, розміщується в резонаторі, який складається з двох паралельних дзеркал. Якщо в результаті одного із спонтанних переходів атомів з мета­стабільного рівня на основний виникає фотон з енергією hn₂₁= Е₂– Е₁, то при поширенні його в бік одного із дзеркал фотон викликає індуковане випромінювання і до дзеркала підходить ціла лавина фотонів з енергією hn₂₁кожний. Після відбиванння від дзеркала лавина фотонів поширю­ється у протилежному напрямку, водночас змушуючи висвітлюватися з метастабільного рівня збуджені атоми, які залишилися в цьому.

З квантових міркувань генерація світла повинна відбуватися при будь-якій відстані між дзеркалами. Але досвід показує, що вона виникає тільки при певній довжині L резонатора, яка кратна цілому числу півхвиль:

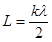. (16.14)

За цієї умови різниця ходу між хвилею, яка виникла, і хвилею, яка відбилася від двох дзеркал, є рівною цілому числу довжин хвиль, і на виході підсилювача відбувається додавання амплітуд світлових хвиль.

Розглянутий принцип підсилення і генерації електро-магнітного випромінювання був запропонований російськими фізиками радянської доби Н.Г.Басовим і А.М.Прохоровим і одночасно американським фізиком Ч.Таун­сом. За роботи в цій галузі Н.Г.Басов, А.М.Прохоров в 1959 році були нагород­жені Ленінською премією і разом з Ч.Таунсом в 1964 році їм присуджена Нобелівська премія.